Actividades: 1ra Evaluación
Actividades: 2da Evaluación
Resumen Python: conceptos y librerías
Formato de Tareas, talleres
Algoritmos: matg1052.py
Actividades: 1ra Evaluación
Actividades: 2da Evaluación
Resumen Python: conceptos y librerías
Formato de Tareas, talleres
Algoritmos: matg1052.py
Ejercicios - Evaluaciones (324)
Ejemplos - Soluciones (146)
Tema 3 (35 puntos) Use el método de diferencias finitas divididas para la ecuación diferencial parcial, también conocida como Poisson, para aproximar la solución de:
\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = x e^{y}
| 0 < y < 1 | u(0,y) = 0 | u(2,y) = 2ey |
| 0 < x < 2 | u(x,0) = x | u(x,1) = xe1 |
Utilice diferencias finitas para las variables independientes x,y
Considere la cantidad de tramos por eje como n=6 en x, m=5 en y, con tolerancia de 10-5.
a. Plantee las ecuaciones discretas a usar un método numérico en un nodo xi, yj
b. Realice la gráfica de malla, detalle los valores de i, j, xi, yj
c. Desarrolle y obtenga el modelo discreto para u(xi,yj)
d. Determine el valor de Lambda λ
e. Adjunte los archivos del algoritmo.py, resultados.txt, gráficas.png
Rúbrica: Selección de diferencias finitas divididas (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos)
Referencia: Burden 10Ed ejemplo 12.2 p550
Tema 2 (35 puntos) Para el sistema de ecuaciones mostrado, encuentre la solución usando el método de Jacobi usando como vector cero como inicial.
x1 − x2 + x3 + 3x4 = 1
x1 + 4x2 − x3 − x4 = −1
−x1 − x2 + 5x3 + x4 = 0
4x1 + x2 − x3 + x4 = −2
a. Presente la matriz aumentada y Muestre los pasos para el pivoteo parcial por filas.
b. Desarrolle las expresiones para resolver mediante el método iterativo de Jacobi.
c. Realice al menos 3 iteraciones con expresiones completas, indicando el error por iteración.
d. Analice la convergencia del método y resultados obtenidos.
e. Determine el número de condición y comente su relación sobre los resultados.
f. Adjunte los archivos del algoritmo y resultados de computadora utilizados.
Rúbrica: Literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos). literal e (5 puntos). literal f (5 puntos)
Referencia: Burden 9Ed ejercicio 7.3.c p459
Tema 1 (35 puntos) A menudo, el crecimiento de una población se puede modelar sobre periodos breves al asumir que aumenta de manera continua con el tiempo a una tasa proporcional al número actual en ese momento.
N(t) = N_0 e^{\lambda t} + \frac{v}{\lambda}\left( e^{\lambda t} -1 \right)
Si se permite inmigración a una tasa constante v, la ecuación N(t) mostrada estima el número de la población en el tiempo t.
Suponga λ denota la tasa constante de natalidad. En un inicio, cierta población tiene N(0)=1 millón de personas, que v=124000 personas inmigran a la comunidad durante el primer año. Que al final del primer año N(1)=1364000. Encuentre la tasa de natalidad λ para el primer año. 
a. Plantear el ejercicio para el eje λ o variable independiente
b. Indique y verifique el intervalo [a,b] a usar en el ejercicio
c. Desarrolle al menos tres iteraciones usando un método para búsqueda de raíces, las expresiones deben ser completas en cada iteración, con los valores usados en cada una.
d. Indique el error en cada iteración.
e. Describa si el método converge y observe los resultados de las iteraciones realizadas.
f. Adjunte en “aulavirtual” los resultados.txt y gráficas.png realizadas con el algoritmo.py
Nota: Si la mitad de la población son mujeres y todas pudiesen tener un hijo, la tasa de natalidad en un periodo de gestación de un año será como máximo del 50 por ciento (0.5).
Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos), literal f (5 puntos).
Referencia:[1] Burden 10Ed ejemplo 1 p35
[2] https://revistacomunicacion.com/2022/03/07/imagenes-y-representaciones-visuales-de-la-migracion%EF%BF%BC/
[3] Planeta Tierra – Población, ciudades y migración (Cap. 8). La Casa Encendida. 2 abril 2020. https://www.youtube.com/watch?v=h2spokNWN50
[4] Migrantes, la gran mayoría latinos, colapsan la Gran Manzana- DW español. 22-Sept-2023.
Tema 3 (30 puntos) Un cuadrado dieléctrico de 2 cm de lado donde los bordes están a tierra, 0 Voltios, y el vértice opuesto está a 80V. Calcular la distribución de potencial, suponiendo que la densidad de carga f(x,y) es nula.
\frac{\partial^2 \phi}{\partial x^2} + \frac{\partial^2 \phi}{\partial y^2} =0
Condiciones de contorno se muestran junto con la ecuación diferencial parcial
\phi (x,0) = \phi(0,y)=0
\phi (x,2) = 40x
\phi (2,y) = 40y
Suponiendo que se satisface la ley de Ohm, considere Δx=Δy=1/4
Utilice diferencias finitas para las variables independientes x,y
a. Plantee las ecuaciones discretas a usar un método numérico en un nodo i,j
b. Realice la gráfica de malla, detalle los valores de i, j, xi, yj
c. Desarrolle y obtenga el modelo discreto para Φ(xi,yj)
d. Determine el valor de Lambda λ
e. Adjunte los archivos del algoritmo.py, resultados.txt, gráficas.png
Rúbrica: Selección de diferencias finitas divididas (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos)
Referencia: Chapter 13: Partial Differential Equations (Part 2 - Elliptic PDEs). Lindsey Westover. 18 Marzo 2021.
Tema 2 (35 puntos) El modelo de crecimiento económico de Solow-Swan describe cómo el capital por trabajador k cambia con el tiempo dk/dt. 
\frac{\delta k}{\delta t} = s f(k) -(d+n)k
f(k) = k^{\alpha}
El cambio del capital por trabajador depende de la inversión, la depreciación d y el crecimiento de la población n.
El primer término aumenta el capital por medio de la inversión por trabajador, s es la tasa de ahorro y f(k) es la función de producción.
El siguiente término disminuye el capital por la depreciación d de equipos, junto con el capital necesario para equipar a los nuevos trabajadores n.
Una propiedad en el modelo de Solow indica que el capital por unidad de trabajo efectivo f(k) muestra rendimientos marginales decrecientes del capital.
En países desarrollados α=0.3, mostrando que el 30% del ingreso nacional total se atribuye al factor de producción de capital como edificios, maquinaria y equipos, mientras que el 70% restante se atribuye al factor de producción trabajo, sueldos y salarios. Considere s=0.15, d=0.05, n=0.015, k(0)=1.
a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden
b. Desarrolle tres iteraciones con expresiones completas para k(t) con tamaño de paso h=0.2 meses
c. Realice una observación sobre el resultado, a lo largo del tiempo para al menos 60 meses usando el algoritmo.
d. Adjunte algoritmo.py, resultado.txt y gráfica.png.
Rúbrica: literal a (5 puntos), literal b (20 puntos), literal c (5 puntos), literal d (5 puntos)
Referencia: [1] Solow-Swan Model. Sean McClung. 8 abril 2025. https://inomics.com/terms/solow-swan-model-1548564
[2] Modelo de crecimiento de Solow. https://es.wikipedia.org/wiki/Modelo_de_crecimiento_de_Solow
[3] The Solow Model and the Steady State. Marginal Revolution University. Apr 12, 2016. https://www.youtube.com/watch?v=LQR7rO-I96A
[4] Human Capital & Conditional Convergence. Marginal Revolution University. Apr 26, 2016. https://www.youtube.com/watch?v=SVWX4Xjl4Os
[5] The Solow Model and Ideas. Marginal Revolution University. May 3, 2016.
Ejercicio: 2Eva_2025PAOI_T2 EDO Modelo económico de Solow-Swan
El modelo de crecimiento económico de Solow-Swan describe cómo el capital por trabajador k cambia con el tiempo dk/dt .
\frac{\delta k}{\delta t} = s f(k) -(d+n)k
f(k) = k^{\alpha}
La EDO es de primera derivada o primer orden, en la que se sustituyen los valore de las constantes y f(k)
f(t,k) = \frac{\delta k}{\delta t} = 0.15 k ^{0.3}-(0.05+0.015)k
Tiene como variable independiente el tiempo t, y como variable dependiente k.
Para evitar repetir la variable k en el algoritmo junto a Runge-Kutta, se cambia la variable por x:
f(t,y) = 0.15 y ^{0.3}-(0.05+0.015)y
Desarrolle tres iteraciones con expresiones completas para k(t) con tamaño de paso h=0.2 meses, que se aplica al algoritmo EDO dy/dx con Runge-Kutta de 2do Orden
K_1 = h f(t_i,y_i)
K_2 = h f(t_i+h, y_i + K_1)
y_{i+1} = y_i + \frac{K_1+K_2}{2}
t_{i+1} = t_i + h
itera=0, ti= 0, yi=k(0)=1
K_1 = 0.2 \left( 0.15 (1) ^{0.3}-(0.05+0.015)(1) \right) =0.017
K_2 = 0.2 \left( 0.15 (1+0.017) ^{0.3}-(0.05+0.015)(1+0.017) \right) =0.016931
y_{1} = 1+ \frac{0.017+0.016931}{2} = 1.016966
t_{1} = 0 + 0.2 = 0.2
itera = 1
K_1 = 0.2 \Big( 0.15 (1.016966) ^{0.3}
-(0.05+0.015)(1.016966) \Big) =0.016931
K_2 = 0.2 \Big( 0.15 (1.016966+0.016931) ^{0.3}
-(0.05+0.015)(1.016966+0.016931) \Big)=0.016861
y_{2} = 1.016966 + \frac{0.016931+0.016861}{2} =1.033862
t_{2} = 0.2 + 0.2 = 0.4
itera = 2
K_1 = 0.2 \left( 0.15 (1.033862) ^{0.3}-(0.05+0.015)(1.033862) \right) =0.016861
K_2 = 0.2 \Big( 0.15 (1.033862+0.016861) ^{0.3}
-(0.05+0.015)(1.033862+0.016861) \Big)=0.016789
y_{3} = 033862 + \frac{0.016861+0.016789}{2}
t_{3} = 0.4 + 0.2 = 0.6
Resultados con el algoritmo:
EDO dy/dx con Runge-Kutta 2 Orden i, [xi, yi, K1, K2] 0 [0. 1. 0. 0.] 1 [0.2 1.016966 0.017 0.016931] 2 [0.4 1.033862 0.016931 0.016861] 3 [0.6 1.050687 0.016861 0.016789] 4 [0.8 1.06744 0.016789 0.016716] 5 [1. 1.084119 0.016716 0.016642] 6 [1.2 1.100723 0.016642 0.016567] 7 [1.4 1.117252 0.016567 0.01649 ] 8 [1.6 1.133703 0.01649 0.016413] 9 [1.8 1.150077 0.016413 0.016334] 10 [2. 1.166371 0.016334 0.016255] ... 295 [5.900000e+01 3.121417e+00 1.647361e-03 1.632629e-03] 296 [5.920000e+01 3.123042e+00 1.632695e-03 1.618093e-03] 297 [5.940000e+01 3.124653e+00 1.618158e-03 1.603683e-03] 298 [5.960000e+01 3.126249e+00 1.603748e-03 1.589400e-03] 299 [5.980000e+01 3.127832e+00 1.589464e-03 1.575241e-03] 300 [6.000000e+01 3.129400e+00 1.575305e-03 1.561206e-03]
gráfica para 60 periodos completos con h=0.2
# EDO dy/dx. M todo de RungeKutta 2do Orden # estima la solucion para muestras espaciadas h en eje x # valores iniciales x0,y0, entrega tabla[xi,yi,K1,K2] import numpy as np def rungekutta2(d1y,x0,y0,h,muestras, vertabla=False,precision=6): '''solucion a EDO dy/dx, con Runge Kutta de 2do orden d1y es la expresi n dy/dx, tambien planteada como f(x,y), valores iniciales: x0,y0, tama o de paso h. muestras es la cantidad de puntos a calcular. ''' tamano = muestras + 1 tabla = np.zeros(shape=(tamano,2+2),dtype=float) tabla[0] = [x0,y0,0,0] # incluye el punto [x0,y0] xi = x0 # valores iniciales yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (K1+K2)/2 xi = xi + h tabla[i] = [xi,yi,K1,K2] if vertabla==True: np.set_printoptions(precision) print( 'EDO dy/dx con Runge-Kutta 2 Orden') print('i, [xi, yi, K1, K2]') for i in range(0,tamano,1): print(i,tabla[i]) return(tabla) # PROGRAMA PRUEBA ------------------- # INGRESO # d1y = y' = f, d2y = y'' = f' d1y = lambda t,k: 0.15*k**(0.3)-(0.05+0.015)*k x0 = 0 y0 = 1 h = 0.2 muestras = int(60/h) # PROCEDIMIENTO tabla = rungekutta2(d1y,x0,y0,h,muestras, vertabla=True) xi = tabla[:,0] yiRK2 = tabla[:,1] # SALIDA #print(' [xi, yi, K1, K2]') #print(tabla) # GRAFICA import matplotlib.pyplot as plt plt.plot(xi,yiRK2) plt.plot(xi[0],yiRK2[0], 'o',color='r', label ='[t0,k0]') ##plt.plot(xi[1:],yiRK2[1:], ## 'o',color='m', ## label ='[xi,yi] Runge-Kutta') plt.title('EDO dk/dt: Solow-Swan') plt.xlabel('t') plt.ylabel('k') plt.legend() plt.grid() plt.show()
.
Tema 1 (35 puntos) Un centroide es un promedio ponderado, como el centro de gravedad, pero ponderado con una propiedad geométrica como el área o el volumen, y no con una propiedad física como el peso o la masa. 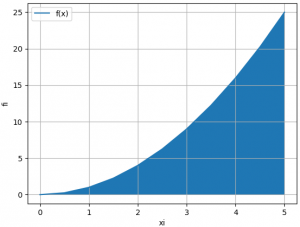
Esto significa que los centroides son propiedades de formas puras, no de objetos físicos. Para el caso particular dado en f(x), los resultados de los integrales permiten obtener las coordenadas del punto medio:
| \bar{x} = \frac{Q_y}{A} | \bar{y} = \frac{Q_x}{A} |
| Q_y = \int x dA = \int_0^5 x^3 dx | Q_x = \int ydA = \int_0^5 \frac{x^4}{2} dx |
| A = \int f(x) dx = \int_0^5 x^2 dx |
Donde Qx, Qy corresponden al primer momento de área con respecto a cada eje. Realice el planteamiento de los integrales considerando que:
a. Para el integral con Qy use fórmulas de Simpson con al menos 3 tramos, mientras que
b. Para el integral con Qx use Cuadratura de Gauss de dos puntos.
c. Desarrolle las expresiones completas del ejercicio para cada función. Para A seleccione el método numérico de su preferencia.
d. Indique el resultado obtenido para el integral requerido y la cota de error.
e. Determine las coordenadas del centroide según las fórmulas presentadas.
f. Adjunte algoritmo.py, resultado.txt y gráfica.png.
Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos), literal f (5 puntos)
Referencia: [1] Engineering Statics Open and Interactive. Daniel W. Baker, William Haynes. https://engineeringstatics.org/Chapter_07-centroids.html
[2] Centroide de una parábola mediante integración. Ingeniería elemental. 13 octubre 2022.
Ejercicio: 2Eva_2025PAOI_T1 coordenadas centroide por integración numérica
Para el integral con Qy use fórmulas de Simpson con al menos 3 tramos,
Q_y = \int x dA = \int_0^5 x^3 dx
a. Para el intervalo de integración [0,5], al considerar 3 tramos, h = 5/3 que es mayor que 1. Se prefiere h≤1 de tal forma que al calcular los errores, la cota del error disminuya por estar en el orden O(hk), por lo que tramos será al menos 5 obteniendo h=1.
xi = [ 0, 1, 2, 3, 4, 5]
c. Con 5 tramos, 6 muestras, se usarán Simpson de 3/8 y luego Simpson de 1/3.
I_{3/8} = \frac{3}{8} (1) \left( 0^3+3(1^3)+3(2^3)+3^3\right) = 20.25
I_{1/3} = \frac{1}{3} (1) \left( 3^3+4(4^3)+5^3\right) = 136
d. Q_y =I_{3/8} + I_{1/3} = 20.25+136 =156.25
cota de error = O(h5)+O(h5) = 2[ O(h5)] = 2(15) = 2
Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] ['S38', 20.25] ['S13', 136.0] tramos iguales en xi: [3 0 0 2 0 0] Integral: 156.25
Para el integral con Qx use Cuadratura de Gauss de dos puntos
Q_x = \int ydA = \int_0^5 \frac{x^4}{2} dx
b. Para cuadratura de Gauss, se tomarían al menos 3 tramos, dado que la cota de error por truncamiento se aproxima con la ≅ f(4)( x )
xi = [ 0, 5/3, 10/3, 5]
c. intervalo [0, 5/3]
x_a = \frac{5/3+0}{2} - \left( \frac{1}{\sqrt{3}} \right) \frac{5/3-0}{2} =0.352208
x_b = \frac{5/3+0}{2} + \left( \frac{1}{\sqrt{3}}\right) \frac{5/3-0}{2} =1.314458
I_0 = \frac{5/3-0}{2} \left( f(x_a) +f(1.314458) \right)
= \frac{5/3-0}{2} \left( \frac{(0.352208)^4}{2} +\frac{(1.314458) ^4}{2} \right) = 1.2502
d. usando el algoritmo se puede obtener el resultado de:
[xa,xb,f(xa),f(xb)],area [0.352208, 1.314458, 0.007694, 1.492648] 1.250285 [xa,xb,f(xa),f(xb)],area [2.018874, 2.981125, 8.306298, 39.490340] 39.830532 [xa,xb,f(xa),f(xb)],area [3.685541, 4.647791, 92.251874, 233.322542] 271.312014 Integral: 312.39283264746234
se plantea usando Simpson de 3/8 o cualquier otro método numérico. con h=1
xi = [ 0, 1, 2, 3, 4, 5]
A = \int f(x) dx = \int_0^5 x^2 dx
I_{3/8} = \frac{3}{8} (1) \left( 0^2+3(1^2)+3(2^2)+3^2\right) = 9
I_{1/3} = \frac{1}{3} (1) \left( 3^2+4(4^2)+5^2\right) = 32.6666
d. Q_y =I_{3/8} + I_{1/3} = 9+32.6666 =41.6666
cota de error = O(h5)+O(h5) = 2[ O(h5)] = 2(15) = 2
usando el algoritmo se obtiene:
Fórmulas compuestas, tramos: 5 métodos 3:Simpson3/8, 2:Simpson1/3, 1:Trapecio, 0:usado tramos iguales en xi: [3 0 0 2 0 0] ['S38', 9.0] ['S13', 32.666666666666664] tramos iguales en xi: [3 0 0 2 0 0] Integral: 41.666666666666664
e. Determine las coordenadas del centroide según las fórmulas presentadas.
\bar{x} = \frac{Q_y}{A}= \frac{156.25}{41.6666} = 3.75
\bar{y} = \frac{Q_x}{A}= \frac{312.5}{41.6666} = 7.5