1raEva 2016-2017-2018 – Página 2

2017-12-022020-05-10

1Eva_IIT2017_T3 Circuito eléctrico

1ra Evaluación II Término 2017-2018. 28/Noviembre/2017. MATG1013

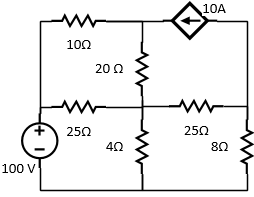
Tema 3. (25 puntos) El sistema de ecuaciones que sigue se generó por medio de aplicar la ley de malla de corriente al circuito de la figura.

\begin{cases} 55 I_1 - 25 I_4 = -200 \\ -37 I_3 - 4 I_4 = -250 \\ -25 I_1 - 4 I_3 + 29 I_4 = 100 \\ I_2 = -10 \end{cases}

a) Use el método de eliminación de Gauss para resolver el sistema

b) Use el método de Jacobi y determine el número de iteraciones para ε=0.01

c) Si el coeficiente 55 se cambia a 54.9, encuentre el error relativo de la aproximación en el literal a.

Rúbrica: Aplicación del método de eliminación de Gauss hasta 10%, Uso del método de Jacobi hasta 5% y determinación del número de iteraciones hasta 5%, Calculo del residuo y cota del error relativo hasta 5%.

A = [[ 55.0, 0,  0, -25],
     [  0  , 0,-37,  -4],
     [-25  , 0, -4,  29],
     [  0  ,  1, 0,   0]]

B = [-200,-250,100,-10]

2017-12-02

1Eva_IIT2017_T2 Ecuaciones no lineales

1ra Evaluación II Término 2017-2018. 28/Noviembre/2017. MATG1013

Tema 2. (25 puntos) Determine una raiz de las ecuaciones no lineales simultaneas siguientes:

y = – x² + x + 0.75
y + 5xy = x²

a) Bosqueje una gráfica y seleccione X⁽⁰⁾

b) Use el método de Newton en dos variables y realice tres iteraciones.

Rúbrica: Bosquejar la gráfica hasta 5%, Plantear el método hasta 5%, Calcular el Jacobiano hasta 5% Hacer tres iteraciones, estimando el error hasta 10%.

2017-12-02

1Eva_IIT2017_T1 Aproximar a polinomio usando puntos

1ra Evaluación II Término 2017-2018. 28/Noviembre/2017. MATG1013

Tema 1. (25 puntos) Se sabe que f ∈ C³[a, b] y tiene la siguiente tabla:

x	f(x)
0	1
0.2	1.6
0.4	2.0

a) Encuentre el polinomio de Taylor de grado 2 alrededor de X₀ = 0.2 para aproximar a f(x)

b) Aproxime $\int_{0}^{0.4}f(x)dx$ por medio de $\int_{0}^{0.4}P_{2}(x)dx$
Estime el error suponiendo que $f'''(\epsilon ) =1$

Rúbrica: Plantear el polinomio hasta 5%, hallar las derivadas hasta 10%, hallar la integral hasta 5% hallar el error hasta 5%.

2017-12-02

1Eva_IT2017_T4 Componentes eléctricos

1ra Evaluación I Término 2017-2018. 26/junio/2017. MATG1013

Tema 4. (25puntos)

https://es.dreamstime.com/tablero-electr%C3%B3nico-de-la-tv-image120402048 — Tablero electrónico de la TV. Sistema, tarjeta

Un supervisor revisa la producción de tres tipos de componentes eléctricos.

Para ellos se requieren tres clases de materiales como se indica en la tabla adjunta:

	Material 1	Material 2	Material 3
Componente 1	5	9	3
Componente 2	7	7	16
Componente 3	9	3	4

a) Si cada semana se dispone de un total de 945 gramos de material 1, 987 gramos de material 2 y 1049 gramos de material 3, ¿Cuántos componentes a lo sumo pueden producirse por semana? (Solo plantear)

b) Si se resuelve con el método de eliminación de Gauss, ¿Cuántas multiplicaciones/divisiones como máximo se realizan?

c) Si se resuelve con el método de Jacobi, encuentre la norma infinita de T y comente sobre la convergencia.

d) Resuelva utilizando el método de Gauss-Seidel, realice tres iteraciones y estime el error de la tercera iteración.

Rúbrica: Planteo hasta 5 puntos, Número de multiplicaciones hasta 5 puntos, ‖T‖_∞ hasta 10 (con filas ordenadas), Iteraciones con Gauss Seidel con la estimación del error hasta 5 puntos.

2017-12-02

1Eva_IT2017_T3 Sistema no lineal

1ra Evaluación I Término 2017-2018. 26/junio/2017. MATG1013

Tema 3. (25 puntos) 3. El sistema no lineal

-x(x + 1) + 2y = 18
x – 1 + (y – 6)² = 25

tiene dos soluciones.

a) Aproxime gráficamente las soluciones

b) Utilice el método de Newton Raphson en una variable para aproximar una solución, (realice tres iteraciones).

c) Utilice el método de Newton Raphson en dos variables para aproximar una solución, (realice tres iteraciones) y estime el error de la segunda iteración.

Rúbrica: Soluciones gráficas hasta 5 puntos, Método de Newton hasta 10 puntos, Método que involucra al jacobiano hasta 10 puntos.

2017-12-022020-06-21

1Eva_IT2017_T2 Tanque esférico-volumen

1ra Evaluación I Término 2017-2018. 26/junio/2017. MATG1013

Tema 2 (25 puntos). El volumen V del líquido contenido en un tanque esférico de radio r está relacionado con la profundidad h del líquido por la ecuación

V = \frac{\pi h^{2} (3r-h)}{3}

Es posible desarrollar las siguientes dos fórmulas para él método de punto fijo:

h = \sqrt{\frac{h^{3}+(3V/\pi)}{3r}}

h = \sqrt[3]{3(rh^{2}-V/\pi)}

Si r=1 m y V=0.75 m³, determine si las dos alternativas son estables (convergen), realice las iteraciones para aproximar h con un error menor o igual 0.01 m.

Rúbrica: Cálculo de las derivadas (10 puntos), determinación de la estabilidad (5 puntos), iteraciones con el error (10 puntos).

2017-12-022020-05-01

1Eva_IT2017_T1 Caida de paracaidista

1ra Evaluación I Término 2017-2018. 26/junio/2017. MATG1013

Tema 1. (25 puntos) La velocidad de caída de un paracaidista puede calcularse con la ecuación

v(t) = \frac{gm}{c} \big( 1- e^{-(c/m)t} \big)

donde g = 9.8, m = 50±2 c = 12.5±1.5

a) Construya un polinomio con los puntos t = 0, 3, 5.

b) Evalúe el polinomio para t = 4 y estime el error de truncamiento y el error propagado.

Rúbrica: Construcción del polinomio hasta 10 puntos, Evaluar el polinomio hasta 5 puntos, estimar el error por truncamiento hasta 5 puntos y estimar el error propagado hasta 5 puntos.

2017-11-162023-02-04

1Eva_IT2016_T3_MN Tasa interés anual

1ra Evaluación I Término 2016-2017. 28/junio/2016. ICM02188 Métodos Numéricos

Tema 3. (25 puntos) Se adquiere a maquinaria o equipo para una empresa por $35000, sin pago inicial, con pagos de $5800 por año durante 8 años.

¿Qué tasa de interés está usted pagando?

La fórmula que relaciona el valor presente P, las anualidades A, el número de años n y la tasa de interés i es:

A = P \frac{i(1+i)^{n}}{(1+i)^{n} -1}

a) Plantee la ecuación y encuentre un intervalo de existencia.
b) Encuentre un intervalo de convergencia
c) Realice cuatro iteraciones y estime el error

Rúbrica: Ecuación (5 puntos), intervalo existencia (2 puntos), Intervalo de convergencia (10 puntos), iteraciones (5 puntos), estimar error hasta (3 puntos)

Referencias:

La venta de tractores se mantiene. El comercio 24-Oct-2009. https://www.elcomercio.com/actualidad/venta-tractores-mantiene.html

La agricultura familiar campesina toma impulso en la provincia de Loja. Crónica.com.ec 31-ago-2018. https://www.cronica.com.ec/informacion-2/ciudad/item/22626-la-agricultura-familiar-campesina-toma-impulso-en-la-provincia-de-loja

2017-11-162023-02-04

1Eva_IT2016_T2_MN Organismos patógenos en lago

1ra Evaluación I Término 2016-2017. 28/junio/2016. ICM02188 Métodos Numéricos

Tema 2. (25 puntos) Tres organismos patógenos decaen en forma exponencial en aguas de un lago de acuerdo con el siguiente modelo:

p(t) = A e^{-1.5t} + B e^{-0.3t} + C e^{-0.05t}

Estime la población inicial de cada organismo, dadas las mediciones siguientes:

Tiempo (horas)	0.5	1	2	3	4
Población (miles)	6.0	4.4	3.2	2.7	2.2

a) Seleccione los tres primeros puntos y plantee un sistema de 3 ecuaciones.
b) Con el método de Jacobi encuentre la matriz T y comente.
c) Con el método de Gauss Seidel realice tres iteraciones y estime el error.

Rúbrica: Ecuaciones (5 puntos), matriz (5 puntos), comentario (6 puntos), Iteraciones (5 puntos), estimación del error (4 puntos).

Referencia: Cuales son los agentes patógenos del agua.
https://www.ecomol.es/tratamientos/cuales-son-los-agentes-patogenos-del-agua/

2017-11-162023-02-04

1Eva_IT2016_T1_MN. Contaminante en lago

1ra Evaluación I Término 2016-2017. 28/junio/2016. ICM02188 Métodos Numéricos

Tema 1. (25 puntos) El balance de masa de un contaminante en un lago, bien mezclado, se expresa mediante la ecuación:

V\frac{dc}{dt} = W - Qc-kV(\sqrt[3]{c})

Dados los valores de parámetros:

V=1x10⁶ m³, 
Q=1x10⁵ m³/año
W=1x10⁶ g/año
k=0.25m^0.5/g^0.5/año

se quiere hallar la concentración c de estado estable (dc/dt= 0)

a) Utilizando el método de Newton, encuentre un modelo iterativo x=g(x) para aproximar c y un intervalo de existencia y convergencia.

b) Realice las iteraciones presentando el error en cada iteración.

Rúbrica:
a) Hallar g (5 puntos), intervalo de existencia (2 puntos), intervalo de convergencia (6 puntos)
b) Iteraciones hasta (8 puntos), estimación del error hasta (4 puntos)