1ra Evaluación I Término 2008-2009. 8/Julio/2008. ICM00158
Tema 3. Dada la tabla:
| t | v(t) |
|---|---|
| 3 | 65.041 |
| 5 | 64.385 |
| 7 | y |
| 9 | 63.210 |
| x | 62.576 |
| 13 | 61.993 |
| 15 | 61.417 |
Aproximar los valores de x,y con ayuda de polinomios de Lagrange
1Eva_IT2008_T2 Temperatura en placa
1ra Evaluación I Término 2008-2009. 8/Julio/2008. ICM00158
Tema 2. La temperatura de una placa está dada por la temperatura de sus bordes, en cada nodo de la malla formada, la temperatura es igual al promedio de los nodos contíguos (arriba, abajo, derecha e izquierda) como se indica en el diagrama adjunto.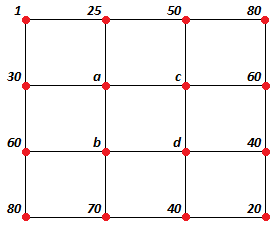
a) Plantee el sistema de ecuaciones asociado para hallar las temperaturas en los nodos interiores de la malla.
b) Utilice el método de eliminación de Gauss con una aritmética de 4 dígitos para aproximar la solución del sistema en el literal a.
1Eva_IT2008_T1 Raíz de función(f)
1ra Evaluación I Término 2008-2009. 8/Julio/2008. ICM00158
Tema 1. Dada la fórmula:
\Big(\sqrt{f}\Big) ln \Bigg( R\frac{\sqrt{f}}{2.51} \Bigg) - 1.1513 = 0Determinar el valor de f con un aproximación del orden de 10-5 para R=5000
1Eva_IIIT2007_T3 Factorar polinomio
1ra Evaluación III Término 2007-2008. 3/Marzo/2008. ICM00158
Tema 3. Se requiere factorar el polinomio:
P_3(x) = 2x^3-5x^2 + 3x-0.1 P_3(x) = (x - r_1)(x - r_2)(x - r_3)Utilizando el siguiente procedimiento:
a. Calcule r1 resolviendo P3(x) = 0 con Newton, ε = 0.0001
b. Obtenga el polinomio cociente Q2(x), a partir de P3(x) = (x – r1)Q2(x)
c. Calcule r2 y r3 de la ecuación Q2(x) = 0
d. Escriba los otros factores de Q2(x) = (x – r2)(x – r3)
Observe la gráfica del problema para la solución
1Eva_IIIT2007_T2 Función Cobb-Douglas
1ra Evaluación III Término 2007-2008. 3/Marzo/2008. ICM00158
Tema 2. La función de producción llamada Cobb-Douglas relaciona funcionalmente a los insumos de capital y trabajo necesarios para producir de la manera más óptima de una determinada cantidad de un bien.
Y = f(K,L) es la cantidad máxima del bien que se puede producir dados los insumos utilizados de capital y trabajo. K y L representan las cantidades de capital y trabajo respectivamente.
En la industria de lácteos se han observado los siguientes valores óptimos de producción Y (en miles de Kg) para diferentes valores de L (número de trabajadores) y capital invertido K (en miles de dólares).
| L\K (miles $) | 10 | 20 | 30 | 40 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 10 | 11.0000 | 13.0813 | 14.4768 | 15.5563 |
| 20 | 18.4997 | 22.0000 | 24.3470 | 26.1626 |
| 30 | 25.0746 | 29.8189 | 33.0000 | 35.4608 |
a. Determinar usando el polinomio de interpolación de Lagrange,
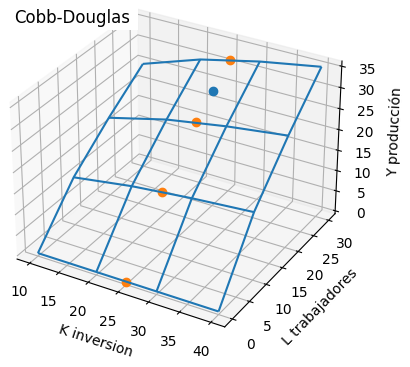¿cuál será la producción óptima de lácteos en una empresa que emplea 25 trabajadores y que invierte un capital de $ 25000 en el plan de producción?
b. Una empresa que tiene 25 trabajadores desea producir 30000 Kg de lácteos. ¿cuánto dinero deberá invertir?, use el polinomio de interpolación y el método de Newton-Raphson con una precisión de 10-5
a.1 Plantear y Desarrollar las expresiones de al menos dos polinomios de Lagrange por filas de la tabla. Los demás puede completar con el algoritmo.
a.2 Use el resultado de cada polinomio para evaluar con K=25. Con los datos de la columna K=25, genere un nuevo polinomio p(K=25)(L) para usarlo para encontrar el valor de Y con L=25.
b.1 Realice el planteamiento del ejercicio, para L= 25, es decir ahora por columnas y obtenga el polinomio p(L=25)(K).
b.2 Plantear usando el polinomio Y(K) = p(L=25)(K) con el método de Newton-Raphson, que encuentre el valor de inversión K para una producción Y.
b.3 Desarrolle las expresiones para tres iteraciones.
b.4 Analice la convergencia del método.
Adjunte sus algoritmos.py, resultados.txt y gráficas.png.
Rúbrica: literal a.1 (10 puntos), literal a.2 (5 puntos)m literal b.1 (5 puntos), b.2(5 puntos), b.3 (5 puntos)
Referencia: Wikipedia/Cobb-Douglas
# INGRESO M = [[ 0, 0, 0, 0 ], [11.0000, 13.0813, 14.4768, 15.5563], [18.4997, 22.0000, 24.3470, 26.1626], [25.0746, 29.8189, 33.0000, 35.4608]] li = [0, 10, 20, 30] kj = [10, 20, 30, 40] l_busca = 25 # trabajadores k_busca = 25 # inversion en miles de $
1Eva_IIIT2007_T1 Container: Cocinas y Refrigeradoras
1ra Evaluación III Término 2007-2008. 3/Marzo/2008. ICM00158
Tema 1. En un container se transportaron cocinas y refrigeradoras.
Cada cocina pesa 100Kg y cada refrigeradora 200Kg.
Por otro lado, una cocina ocupa un espacio de 1.05 m3 y cada refrigeradora 2 m3.
En total entre cocinas y refrigeradoreas se registró un peso de 1000Kg y ocuparon juntas un espacio de 10.4 m3.
Se desea conocer cuántas cocinas y refrigeradoras se transportó en el container.
a. Plantear este problema como el de un sistema de ecuaciones y resolverlo con un método directo (Gauss), usar aritmética de 4 dígitos.
b. El encargado de transporte se equivocó, y en realidad cada cocina ocupa un espacio de 1.1 m3. Encuentre nuevamente la solución.
c. El sistema de ecuaciones usado ¿Es bién o mal condicionado?
1Eva_IIT2007_T3 Interpolación inversa, encontrar xi para fi dado
1ra Evaluación II Término 2007-2008. 4/Diciembre/2007.
ICM00158
Tema 3. Dado los datos de una función:
f(0.50) = 1.648
f(0.65) = 1.915
f( x ) = 2.117
f(0.80) = 2.225
f(0.95) = 2.5857
Determinar el valor de x, usando interpolación inversa.
xi = [0.50 , 0.65 , x, 0.80 , 0.95 ]
fi = [1.648, 1.915, 2.117, 2.225, 2.5857]
a. Plantear el ejercicio describiendo los criterios a usar para el polinomios para el eje y.
b. Desarrolle el método sobre los puntos seleccionados con las expresiones completas desarrolladas con el algoritmo.
c. Presentar el polinomio resultante y la gráfica usando la resolución requerida para el estudio.
d. Adjunte los archivos: algoritmos.py, resultados.txt y gráfica.png del polinomio.
Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (5 puntos), literal d (5 puntos).
1Eva_IIT2007_T2 Aplicar Gauss-Seidel 6×6
1ra Evaluación II Término 2007-2008. 4/Diciembre/2007. ICM00158
Tema 2. Dadas las matrices:
A = [[7.63, 0.30, 0.15, 0.50, 0.34, 0.84],
[0.38, 6.40, 0.70, 0.90, 0.29, 0.57],
[0.83, 0.19, 8.33, 0.82, 0.34, 0.37],
[0.50, 0.68, 0.86, 10.21, 0.53, 0.70],
[0.71, 0.30, 0.85, 0.82, 5.95, 0.55],
[0.43, 0.54, 0.59, 0.66, 0.31, 9.25]]
B = [ -9.44, 25.27, -48.01, 19.76, -23.63, 62.59]
a) Escribir los sistemas AX=B y X=TX+C
b) Determine ||A||∞, y ||T||∞
c) Establezca la solución con el método de Gauss-Seidel con una tolerancia de 10-5
1Eva_IIT2007_T1 Distribución Binomial acumulada
1ra Evaluación II Término 2007-2008. 4/Diciembre/2007. ICM00158
Tema 1. Un modelo de uso frecuente en teoría de probabilidad es la distribución binomial acumulada, cuya fórmula es:
F = \sum_{t=0}^{k} \binom{n}{t} p^t (1-p)^{n-t}Con la fórmula de Newton-Raphson, calcule con cuatro decimales exactos el valor de p tal que F=0.4, dado que n=5 y k=1
Nota: El valor de p debe ser un número real entre 0 y 1
a. Plantear el ejercicio para encontrar h para un t dado, muestre el intervalo de búsqueda y una gráfica.
b. Desarrolle usando el método de Newton-Raphson para tres iteraciones y tolerancia milimétrica.
c. Verifique el orden de convergencia y observe sus resultados usando el algoritmo.
Rúbrica: Planteamiento (5 puntos), iteraciones y error (15 puntos), análisis de la convergencia (5 puntos). observación de resultados, algoritmo y gráficas adjuntos (5 puntos).