Tema 1. Resolver el siguiente problema de valor inicial:
y'+ \frac{2}{t}y = \frac{\cos (t)}{t^2} y(\pi)=0, t\gt 0a. Determinar f(t,y)
b. Escribir el algoritmo de Runge-Kutta de 4to orden para la función definida en el literal a.
c. Presentar la tabla de resultados para el tamaño de paso h=0.2, con i = [0,9]
Tema 3. La placa plana mostrada en la figura está construida con cierto metal, y se ha determinado que la temperatura en los bordes de la placa es la que se indica en la figura.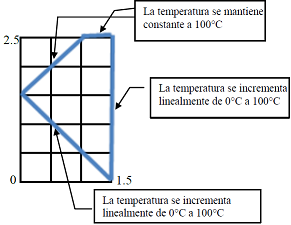 
Ademas de tiene que el término no homogéneo asociado a la ecuación elíptica respectiva es f(x,y)=20
\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = fEl problema consiste en determinar la temperatura en los puntos del interior de la placa en la malla que se muestra en la figura.
a. Determinar el algoritmo en diferencias finitas que resuelve el problema
b. Plantear el sistema de ecuaciones lineas que resuelve el problema
c. Utilice el método de Gauss para resolver el sistema de ecuaciones generado
Tema 2. La ecuación de un movimiento angular está dada por
y'' + 10 \sin (y) =0 0\leq t \leq 1 y(0)=0, y'(0)=0.1Empleando el método de Runge-Kutta de 4to orden generalizado y un paso de 0.25, aproximar la solución de la ecuación en t=0.50
Referencia: Chapra 28.4 p842 pdf 866
Tema 1. Aproximar el perímetro de la región ubicada en el primer cuadrante, acotada por los ejes coordenados y la curva
\begin{cases} x = 2 cos(t) \\ y = \sqrt{3} \sin{(t)} \end{cases} t \in \Big[0, \frac{\pi}{2}\Big]Utilice la regla compuesta de Simpson con n=8
