Algoritmos101

Cursos Python

Categoría: 2da Evaluación

  • 2Eva_IIT2007_T2_AN EDO Lanzamiento vertical proyectil

    2da Evaluación II Término 2007-2008. 12/Febrero/2008. Análisis Numérico

    Tema 2. Un proyectil de masa = 0.11 Kg es lanzado verticalmente hacia arriba con una velocidad inicial V(0) = 8 m/s.

    El proyectil disminuye su velocidad por efecto de la fuerza de gravedad
    Fg = -mg
    y por la resistencia del aire
    Fr = kv|v|
    donde g = 9.8 m/s2 y k = 0.002 Kg/m.

    La ecuación diferencial de la velocidad está dada por:

    m \frac{\delta v}{\delta t} = -mg - kv|v|

    a. Calcule la velocidad con el método de Runge-Kutta de cuarto orden para

    t = 0.2, 0.4, ... , 1.0 segundos.

    b. Calcule en que tiempo el proyectil alcanzará la altura máxima.

    Referencias:

  • 2Eva_IIT2007_T1 Integral regla Simpson

    2da Evaluación II Término 2007-2008. 12/Febrero/2008. ICM00158

    Tema 1. Use la regla de Simpson para calcular en forma aproximada

    A = \int_0^1 y(x)dx

    Use los puntos de y(x) que se obtienen resolviendo la ecuación diferencial

    y'' - y' - y - x + 1 = 0

    y(0) = 1, y(1) = 2

    con el método de diferencias finitas, h = 0.25

  • 2Eva_IIT2010_T3 Integral impropia

    2da Evaluación II Término 2010-2011. 1/Febrero/2011. ICM00158

    Tema 3. Determinar el valor de la integral impropia:

    \int_0^{1/2} \frac{1}{|2x-1|^{1/3}} \delta x

    Con Simpson, n=4

  • 2Eva_IIT2010_T2 Calcular volumen

    2da Evaluación II Término 2010-2011. 1/Febrero/2011. ICM00158

    Tema 2. Calcule el volumen

    \int\int u(x,y) \delta x \delta y

    en el que u(x,y) está definido con la ecuación diferencial

    \frac{\delta ^2 u}{\delta x^2} + \frac{\delta ^2 u}{\delta y^2} = 4 u = u(x,y) 0\leq x \leq 2 0 \leq y \leq 1

    con las condiciones en los bordes:

    u(0,y) = 40 , 0\lt y \lt 1 u(2,y) = 50 , 0\lt y \lt 1 u(x,0) = 40 + 5x , 0\lt x \lt 2 u(x,1) = 40 + 5x , 0\lt x \lt 2

    Use el método de diferencias finitas para resolver la ecuación diferencial y la fórmula de Simpson para calcular el integral. En todos los cálculos use Δx = Δy = 0.5

  • 2Eva_IIT2010_T1 EDO dy/dt Problema valor inicial

    2da Evaluación II Término 2010-2011. 1/Febrero/2011. ICM00158

    Tema 1. Resolver el siguiente problema de valor inicial:

    y'+ \frac{2}{t}y = \frac{\cos (t)}{t^2} y(\pi)=0, t\gt 0

    a. Determinar f(t,y)

    b. Escribir el algoritmo de Runge-Kutta de 4to orden para la función definida en el literal a.

    c. Presentar la tabla de resultados para el tamaño de paso h=0.2, con i = [0,9]

  • 2Eva_IT2010_T3 EDP elíptica, Placa no rectangular

    2da Evaluación I Término 2010-2011. 31/Agosto/2010. ICM00158

    Tema 3. La placa plana mostrada en la figura está construida con cierto metal, y se ha determinado que la temperatura en los bordes de la placa es la que se indica en la figura. Placa Temp 02

    Ademas de tiene que el término no homogéneo asociado a la ecuación elíptica respectiva es f(x,y)=20

    \frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = f

    El problema consiste en determinar la temperatura en los puntos del interior de la placa en la malla que se muestra en la figura.

    a. Determinar el algoritmo en diferencias finitas que resuelve el problema

    b. Plantear el sistema de ecuaciones lineas que resuelve el problema

    c. Utilice el método de Gauss para resolver el sistema de ecuaciones generado

  • 2Eva_IT2010_T2 EDO Movimiento angular

    2da Evaluación I Término 2010-2011. 31/Agosto/2010. ICM00158

    Tema 2. La ecuación de un movimiento angular está dada por

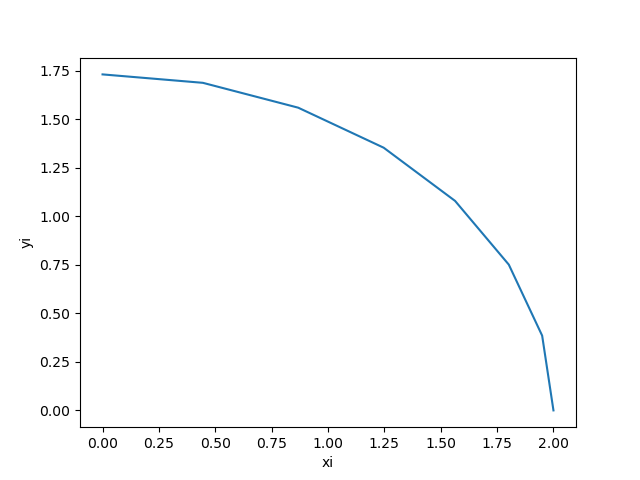
    y'' + 10 \sin (y) =0 0\leq t \leq 1 y(0)=0, y'(0)=0.1

    Empleando el método de Runge-Kutta de 4to orden generalizado y un paso de 0.25, aproximar la solución de la ecuación en t=0.50

    Referencia:  Chapra 28.4 p842 pdf 866

    https://nitanperdida.com/2017/12/24/banos-y-el-columpio-del-fin-del-mundo/
    BAÑOS DE AGUA SANTA Y EL COLUMPIO DEL FIN DEL MUNDO

  • 2Eva_IT2010_T1 Perímetro de región

    2da Evaluación I Término 2010-2011. 31/Agosto/2010. Análisis Numérico

    Tema 1. Aproximar el perímetro de la región ubicada en el primer cuadrante, acotada por los ejes coordenados y la curva

    \begin{cases} x = 2 cos(t) \\ y = \sqrt{3} \sin{(t)} \end{cases} t \in \Big[0, \frac{\pi}{2}\Big]

    Utilice la regla compuesta de Simpson con n=8

    Región acotada 01

  • 2Eva_IT2009_T3_MN Asignar presupuesto a comunidades aledañas

    2da Evaluación I Término 2009-20010. ICM02188 Métodos Numéricos

    Tema 3 (30 puntos) En una región se han agregado 4 nuevas comunidades a las 8 comunidades existentes. Estas 8 comunidades existentes reciben anualmente recursos monetarios (miles de dólares) como se indica en el cuadro adjunto.

    Las 4 nuevas comunidades deberá recibir una cantidad de dinero igual al promedio de las comunidades ubicadas inmediatamente a su alrededor. Estos valores se los ha representado por x1, x2, x3, x4 y deben ser calculados:

    48.2 53.4 x4
    40.5 x1 65.1
    x2 58.0 42.6
    55.4 x3 70.8

    a. Plantee un sistema de ecuaciones para representar y resolver este problema.

    b. Determine si el método iterativo de Jacobi convergerá. Justifique su respuesta.

    c. Comience con un vector nulo y calcule la solución hasta obtener un decimal de precisión. Use el método iterativo de Gauss-Seidel. Escriba los resultados intermedios.

  • 2Eva_IT2009_T2_MN Longitud de perfil de la plancha

    2da Evaluación I Término 2009-20010. ICM02188 Métodos Numéricos

    Tema 2 (30 puntos). plancha Techo Ondulada
    En el techado de las casas se utilizan planchas corrugadas con perfil ondulado.

    Cada onda tiene la forma
    f(x) = sen(x)
    con un periodo de 2π pulgadas.

    El perfil de la plancha tiene 8 ondas y la longitud L de cada onda se puede calcular con la siguiente integral:

    L = \int_0^{2\pi} \sqrt{1+(f'(x))^2} \delta x

    Este integral no puede ser calculado por métodos analíticos.

    Encuentre la longitud del perfil de la plancha. Use la fórmula de Simpson con m=6 para calcular L.

    Técnica para hacer láminas de zinc para tejados. @WonderWeaveINC-nn4rs. 4-diciembre-2024