3raEva 2022-2023-2024 – Página 2

2023-02-072023-02-07

3Eva_2022PAOII_T4 Recesión económica, PIB y diferenciación numérica

3ra Evaluación 2022-2023 PAO II. 7/febrero/2023

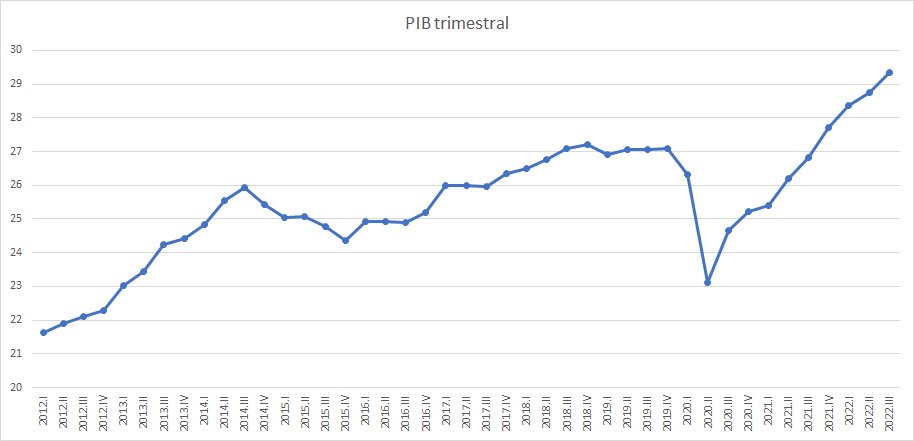
Tema 4. (20 puntos) Las recesiones económicas se caracterizan por presentar una disminución del consumo, de la inversión y de la producción de bienes y servicios. Lo cual provoca, a su vez, que se despidan trabajadores y por tanto, aumente el desempleo. La recesión es también conocida como el periodo de «vacas flacas».

La opinión emitida por Julius Shiskin en un artículo publicado el 28 de agosto de 1975 en el diario New York Times en torno a dos trimestres consecutivos de caída del PIB como plazo definitorio para el considerar una recesión.

a. Plantee y describa los métodos de diferenciación numérica que usen dos y tres puntos para primera derivada.

b. Realice tres iteraciones con los métodos numéricos seleccionados. Describa el tamaño de paso usado en cada método.

c. Compare los resultados del literal anterior y escriba sus observaciones respecto a las cotas de error.

d. Determine los periodos de “recesión económica” para los datos proporcionados entre el año 2012 y 20122. Liste acorde a lo definido por J. Shiskin. Use los algoritmos y adjunte los archivos usados (py,txt,png).

trimestres = ['2012.I', '2012.II', '2012.III', '2012.IV',
 '2013.I', '2013.II', '2013.III', '2013.IV', '2014.I',
 '2014.II', '2014.III', '2014.IV', '2015.I', '2015.II',
 '2015.III', '2015.IV', '2016.I', '2016.II', '2016.III',
 '2016.IV', '2017.I', '2017.II', '2017.III', '2017.IV',
 '2018.I', '2018.II', '2018.III', '2018.IV', '2019.I',
 '2019.II', '2019.III', '2019.IV', '2020.I', '2020.II',
 '2020.III', '2020.IV', '2021.I', '2021.II', '2021.III',
 '2021.IV', '2022.I', '2022.II', '2022.III']

PIB trimestral = [21.622937, 21.908844, 22.106937,
 22.285826, 23.019786, 23.441324, 24.238576, 24.429973,
 24.829431, 25.540887, 25.9404, 25.415613, 25.052739,
 25.086195, 24.779738, 24.371709, 24.913573, 24.926186,
 24.910741, 25.187196, 26.000261, 25.99355, 25.960907,
 26.341144, 26.510612, 26.761827, 27.078404, 27.211165,
 26.914897, 27.058331, 27.054758, 27.080023, 26.314576,
 23.110752, 24.64388, 25.221916, 25.412756, 26.20682,
 26.828611, 27.717679, 28.372038, 28.74092, 29.334581]

Rúbrica: literal a (3 puntos), literal b (9 puntos). literal c(3 puntos) literal d (5 puntos)

Referencia: Recesión económica. Wikipedia. https://es.wikipedia.org/wiki/Recesi%C3%B3n
Recesión económica. economipedia. https://economipedia.com/definiciones/recesion-economica.html

Boletín de Cuentas Nacionales Trimestrales No. 121, valores constantes USD 2007 y corrientes, período : 2000.I – 2022.IIIIT Banco Central del Ecuador (2022) https://contenido.bce.fin.ec/documentos/PublicacionesNotas/Catalogo/CuentasNacionales/Indices/c121122022.htm

2023-02-072024-07-26

3Eva_2022PAOII_T3 EDO cabezal lector en disco duro

3ra Evaluación 2022-2023 PAO II. 7/febrero/2023

Tema 3. (35 puntos) El objetivo de un sistema de Disco duro es posicionar con precisión el dispositivo de lectura en la pista buscada y moverse entre una pista y otra.

Se requiere identificar el plato de disco, el sensor y el controlador.

El disco duro usa un motor DC de imán permanente para posicionar el brazo lector con el sensor en un extremo. Un resorte metálico se usa para permitir que el cabezal flote sobe el disco a una distancia menor a 100nm.

El cabezal toma lectura del flujo magnético y da una señal al amplificador.

Suponiendo que dispone del dispositivo de lectura de precisión, una aproximación del modelo de control del motor con K_a=40, se supone que el brazo es rígido con parámetros como los mostrados, el sistema se puede aproximar como un sistema de orden 2 en el dominio s o en su forma de ecuación diferencial.

Y(s)(s^2+20s+5K_a )=X(s)5K_a

\frac{\delta^2}{\delta t^2 } y(t) + 20 \frac{\delta}{\delta t} y(t) + 5 K_a y(t) = x(t) 5 K_a

y(0) = 0 y’(0) = 0

x(t) = \begin{cases} 0 & t\lt 0 \\ 1 & t≥0 \end{cases}

Encuentre la respuesta del sistema y(t) ante una señal de entrada x(t), con las condiciones iniciales dadas.

a. Plantee la solución usando el método de Runge-Kutta de 2do orden.
b. Desarrolle tres iteraciones para Δt = 0.01
c. Estime el error del modelo usado
d. Realice la gráfica para y(t) para el intervalo de [0,1] segundos. Adjunte los archivos de los algoritmos.py usados para los cálculos, los resultados.txt y gráfica.png

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d y adjuntos (10 puntos)

Referencia: Bishop R. & Dorf R. (2017) 13th Edition. 2.10 sequential Design example: Disk Drive read system. p122.
How do Hard Disk Drives Work? Branch Education. 22 diciembre 2022.

2023-02-072023-02-11

3Eva_2022PAOII_T2 Globo meteorológico espía distancia mas cercana

3ra Evaluación 2022-2023 PAO II. 7/febrero/2023

Tema 2. (20 puntos) Se requiere hacer el seguimiento a la trayectoria del globo aerostático del tema anterior, para descartar las sospechas de espionaje.

Dadas las coordenadas de un lugar considerado como de seguridad nacional p1(x,y)=[25,50] , se requiere revisar la distancia más cercana de la trayectoria y(x) del globo al punto de “interés”.

Se compararía la distancia mínima con el alcance las cámaras y sensores encontrados en los escombros del globo derribado.

Usando la trayectoria obtenida como resultado del tema anterior, se requiere:

a. Plantee el ejercicio describiendo los criterios usados, el método numérico y una tolerancia a usar.

b. Desarrolle el método para encontrar la raíz de la ecuación planteada, con al menos tres iteraciones.

c. Estime la cota de error, compare con la tolerancia descrita en el literal a.

Nota: Si el resultado del tema 1 no es satisfactorio, desarrolle el tema con y(x) = 70sin(0.1πx+0.5)

Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (5 puntos)

2023-02-072023-02-11

3Eva_2022PAOII_T1 Globo meteorológico espía derribado

3ra Evaluación 2022-2023 PAO II. 7/febrero/2023

Tema 1. (25 puntos) En enero del 2023 se detectó un globo aerostático supuestamente espía sobre el territorio soberano de un país, que sobrevoló a 18 Km de altura en la estratosfera y que «no representaba ningún riesgo militar o físico los ciudadanos en la superficie».

Otro país vecino al mismo tiempo hacía seguimiento a otro «posible segundo incidente», se anunció en los medios de comunicación. En el primer caso se decidió no destruir el aparato por el temor de que la caída de sus escombros podría haber sido peligrosa para la superficie y no representaba el globo un peligro inmediato.

Como seguimiento al caso, se requiere describir la trayectoria del globo mediante ecuaciones a partir de las coordenadas de avistamiento reportadas por civiles.

ti    = [11, 12, 14, 15, 17, 19]
x(ti) = [15, 18, 25, 27, 31, 40]
y(ti) = [45, 55, 65, 58, 55, 40]

a. Plantear el ejercicio, describiendo los criterios, método numérico, segmentos a usar en las ecuaciones para realizar la interpolación polinómica de Lagrange.

minimizando oscilaciones del polinomio que puedan resultar en interpretaciones erradas.

b. Realizar el desarrollo analítico de las ecuaciones planteadas y presente el polinomio simplificado.

c. Validar los resultados usando el algoritmo, adjunte los archivos.py, resultados.txt, gráfica.png

Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (10 puntos)

Referencias: Detectan un globo aerostático espía sobre territorio. Rtve.es/Agencias 03/febrero/2023. https://www.rtve.es/noticias/20230203/eeuu-detecta-globo-aerostatico-espia-china-sobre-su-territorio/2420646.shtml

Derriban globo «espía» sobre la costa del Atlántico. DW 04/febrero/2023. https://www.dw.com/es/eeuu-derriba-globo-esp%C3%ADa-chino-sobre-la-costa-del-atl%C3%A1ntico/a-64613403

EE.UU. derriba el presunto globo espía de China. CNN en Español. 4 feb 2023.

Globos chinos en América desatan preocupación mundial. DW Español
DW Español. 10 feb 2023

2022-09-152022-09-15

3Eva_2022PAOI_T3 EDO Modelo de selección híbrida

3ra Evaluación 2022-2023 PAO I. 13/Septiembre/2022

Tema 3. (35 puntos) En genética, el modelo de selección híbrida representa la porción de la población que tiene ciertas características a lo largo del tiempo medido en generaciones (h=1).

Para una población de escarabajos, la rapidez de transferencia que una característica D pasa de una generación a la siguiente está dada por:

\frac{d}{dt}y(t) = k(1-y(t))(a-by(t))

Las constantes a, b y k dependen de las características genéticas estudiadas.

Al inicio del estudio, t=0, se encuentra que la mitad de la población tiene la característica D, y(0)=0.5. El factor k=0.26 considera la trasferencia al combinarse los especímenes “Sin D” y “con D”. Use los valores de a=2 y b=1.

a) Realice el planteamiento del problema de la Ecuación Diferencial Ordinaria usando el método de Runge-Kutta de 4to Orden

b) Desarrolle al menos tres iteraciones usando las expresiones completas.

c) estime la cota de error de la solución.

d) Adjunte el desarrollo completo usando un algoritmo con Python para las próximas 10 generaciones. tabla y gráfica.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d (5 puntos), gráfica(5puntos)

Referencias: Larson. Cálculo aplicado, 7ma Ed. Apéndice C, ejemplo 4. https://college.cengage.com/mathematics/larson/calculus_applied/7e/students/appendices/appendix_c04.pdf
Los mecanismos del cambio. https://www.sesbe.org/evosite/evo101/IIIBMechanismsofchange.shtml.html

2022-09-152022-09-15

3Eva_2022PAOI_T2 Perfil de sendero en montaña

3ra Evaluación 2022-2023 PAO I. 13/Septiembre/2022

Tema 2. (30 puntos) Una persona al recorrer un sendero de ascenso a una montaña, registra en la tabla mostrada, la distancia horizontal desde el punto de partida y la altura del nivel del mar.

Para resumir los datos del perfil de elevación en el sendero en la montaña, se prefiere una descripción mediante un polinomio de interpolación.

a) Plantear el o los polinomios de interpolación para las muestras presentadas para todo el intervalo de la tabla. Indique los criterios usados para el grado del polinomio y los puntos seleccionados que minimicen las distorsiones posibles por el grado polinomio.

b) Desarrolle las expresiones para los polinomios usando el método de Lagrange. (al menos dos polinomios)

c) Determine el error para el polinomio planteado sobre los datos.

d) Adjunte el desarrollo del ejercicio realizado con el algoritmo en Python.

Recorrido (Km)	0,0	1,0	2,0	3,0	4,0	5,0	6,2	7,0	8,0	9,0	10,0	11,0
Altura (m)	4315	4447	4559	4692	4884	5201	5366	5310	5249	5175	5034	4787

Rúbrica: Literal a. criterios (6 puntos), literal b, (12 puntos), literal c (5 puntos), literal d (5 puntos)

Referencia: Ascensión al Chimborazo (6.268m) Andes de Ecuador. Abril 29,2020. https://carrerasdemontana.com/2020/04/29/ascension-al-chimborazo/ ; El último hielero de Ecuador | DW Documental. 28 jul 2018 https://youtu.be/mESOZvOgs5k

xi = [0.0, 1.0, 2.0, 3.0, 4.0, 5.0, 6.2,
      7.0, 8.0, 9.0, 10.0, 11.0]
yi = [4315, 4447, 4559, 4692, 4884, 5201, 5366, 
      5310, 5249, 5175, 5034, 4787]

2022-09-152022-09-15

3Eva_2022PAOI_T1 Objeto no identificado entra y sale del agua

3ra Evaluación 2022-2023 PAO I. 13/Septiembre/2022

Tema 1. (35 puntos) Un objeto sin identificar sale y entra del agua describiendo una trayectoria descrita por la ecuación mostrada en el intervalo para x entre [0, π].

y(x) = e^{-x/3} \sin \Big(x^2 - \frac{\pi}{4} \Big)

Suponga que el nivel del agua se encuentra en y=0.

a) Encuentre un punto de ingreso al agua del objeto, usando el método de la bisección. Realice las expresiones numéricas completas para 3 iteraciones.

b) Determine un punto de salida del agua del objeto, usando el método del punto fijo. Realice las expresiones numéricas completas para 3 iteraciones. Analice la convergencia del método.

c) En cada caso muestre las cotas de error.

d) Adjunte el desarrollo de cada algoritmo en Python

Rúbrica: literal a, planteamiento e intervalo (3 puntos), tres iteraciones (6 puntos), literal b, planteamiento e intervalo (3 puntos), tres iteraciones (6 puntos). convergencia (9 puntos), literal c, (3 puntos). literal d (5 puntos)

Referencia: US releases UFO report with ‘no explanation’ for 143 sightings | DW News. 26 Junio 2021.

Battleship (7/10) Movie CLIP – That’s a Hit (2012) HD