Evaluaciones – Página 2 – Métodos numéricos

2024-02-152024-02-20

3Eva_2023PAOII_T2 perfil de un peón

3ra Evaluación 2023-2024 PAO II. 15/Febrero/2024

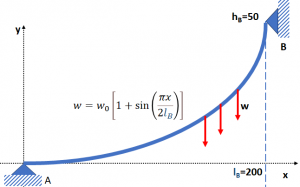
Tema 2 (30 puntos) Las medidas del perfil de un objeto se describen por medio de los siguientes puntos:

x_i	0	3	5	9.985	14.97	17.97	40.04	43.29	51.64560	60
y_i	15	15	13.25	14.155	9.676	9.676	4.64	4.64	8.976	0

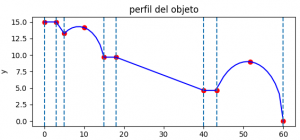a. Plantee el o los polinomios de interpolación P(x) que describan el perfil del objeto en el intervalo
[0, 14.97] . Justifique la selección del método de interpolación polinómica.

b. Desarrolle los polinomios planteados de forma analítica.

c. Estime el mayor error sobre el o los datos en el intervalo [5, 9.985]. Use como referencia la ecuación del círculo del tema anterior.

d. Escriba sus conclusiones y recomendaciones sobre los resultados obtenidos. Adjunte los archivos realizados como algoritmos.py, resultados.txt y gráficas.png

Rúbrica: literal a (9 puntos), literal b (12 puntos), literal c (6 puntos), literal d (3 puntos)

xi=[ 0, 3, 5.  , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60]
yi=[15,15,13.25,14.1552, 9.6768,  9.67,  4.64,  4.64,  8.9768, 0.]

2024-02-152024-10-08

3Eva_2023PAOII_T1 Intersección con círculo

3ra Evaluación 2023-2024 PAO II. 15/Febrero/2024

Tema 1 (30 puntos) Encuentre las raíces de las ecuaciones simultaneas siguientes:

2y+1.75 x= 35.25

(y-7.6)^2 + (x-8.6)^2 = (6.7)^2

a. Use el enfoque gráfico para obtener los valores iniciales. Presente la gráfica realizada con Python.
b. Encuentre un intervalo apropiado para aproximar este valor mediante el método de Newton-Raphson
c. Realice al menos 3 iteraciones de forma analítica, usando tolerancia de 10^-4
d. Realice el análisis de la convergencia del método.
Adjunte los archivos realizados como algoritmos.py, resultados.txt y gráficas.png

Rúbrica: literal a (5 puntos), literal b (5 puntos), iteraciones(9 puntos), errores entre iteraciones (6 puntos), análisis de convergencia (5 puntos).

2024-01-312024-02-04

2Eva_2023PAOII_T3 EDP desarrolle expresión

2ra Evaluación 2023-2024 PAO II. 30/Enero/2024

Tema 3 (30 puntos) Para la siguiente Ecuación Diferencial Parcial con b = 2, resuelva usando las condiciones mostradas

\frac{\partial ^2 u}{\partial x^2} + b\frac{\partial u}{\partial x} = \frac{\partial u}{\partial dt}

0 < x < 1

0 < t < 0.5

Condiciones de frontera:
u(0,t)=0, u(1,t)= 1, 0≤t≤0.5
Condiciones iniciales:
u(x,0)=0, 0≤x≤1

Utilice diferencias finitas centradas y hacia adelante para las variables independientes x,t

a. Plantee las ecuaciones para usar un método numérico en un nodo i,j

b. Realice la gráfica de malla,

c. Desarrolle y obtenga el modelo discreto para u(x_i,t_j)

d. Realice al menos tres iteraciones en el eje tiempo.

e. Estime el error de u(xi,tj) y adjunte los archivos del algoritmo y resultados.

f. Con el algoritmo, estime la solución para b = 0 y b=-4. Realice las observaciones de resultados para cada caso.

Rúbrica: Aproximación de las derivadas parciales (5 puntos), construcción de la malla (5), desarrollo de iteraciones (10), literal e (10 puntos), literal f (5 puntos extra)

Referencia: EDP Parabólicas. Chapra & Canale. 5ta Ed. Ejercicio 30.15. P.904

2024-01-312024-02-04

2Eva_2023PAOII_T2 Cable cuelga entre apoyos A y B

2ra Evaluación 2023-2024 PAO II. 30/Enero/2024

Tema 2 (40 puntos) Un cable cuelga de dos apoyos en A y B.

El cable sostiene una carga distribuida cuya magnitud varía con x según la ecuación

w = w_0 \Big[ 1+ \sin \Big(\frac{\pi x}{2l_B} \Big) \Big]

donde w₀ = 1 000 lbs/ft y T₀. = 0.588345×10⁶.
La pendiente del cable (dy/dx) = 0 en x = 0, que es el punto más bajo del cable.

También es el punto donde la tensión del cable alcanza un mínimo de T₀. La ecuación diferencial que gobierna el cable es

\frac{d^2y}{dx^2} = \frac{w_0}{T_0} \Big[ 1+ \sin \Big(\frac{\pi x}{2l_B} \Big) \Big]

a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b. Desarrolle tres iteraciones para y(x) con tamaño de paso h=0.5

c. Usando el algoritmo, aproxime la solución para x en el intervalo entre [0,200], adjunte sus resultados.txt en la evaluación.

d. Realice sus observaciones sobre los resultados obtenidos sobre la altura y(200) alcanzada en el extremo derecho del cable y lo indicado en la gráfica del enunciado.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c resultados.txt (10 puntos), grafica.png (5 puntos), literal d (5 puntos),

Referencia: Cable entre dos apoyos con carga distribuida. Chapra & Canale. 5ta Ed. Ejercicio 28.21. P849

2024-01-312024-08-09

2Eva_2023PAOII_T1 Volumen por solido de revolución

2da Evaluación 2023-2024 PAO II. 30/Enero/2024

Tema 1 (30 puntos) Los sólidos de revolución se generan al girar una región plana alrededor de un eje.

V = \int_{a}^{b} \pi (f(x))^2 dx

El volumen generado al girar la región de la función f(x) en el intervalo [a,b], se puede calcular como el volumen del disco de radio f(x) y anchura dx.

f(x) = \sqrt{\sin (x/2)}

g(x) = e^{x/3} - 1

Calcule el volumen de revolución generado por la región sombreada de la gráfica que ese encuentra entre: f(x) y g(x).
Las funciones se usan en el intervalo [0.1 , 1.8]:

Realice el planteamiento de las ecuaciones para el ejercicio, considerando que

a. Para el integral con f(x), use formulas de Simpson con al menos 3 tramos, mientras que

b. Para el integral con g(x) use Cuadratura de Gauss de dos puntos con al menos 2 tramos.

c. Desarrolle las expresiones completas del ejercicio para cada función.

d. Indique el resultado obtenido para el área requerida y la cota de error.

e. Determine el volumen de revolución generado por la región sombreada

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (10 puntos), literal d (5 puntos), literal e (5 puntos)

Referencia: [1] Volúmenes de sólidos de revolución. Moisés Villena Muñoz.Capítulo 4 p78. https://www.dspace.espol.edu.ec/bitstream/123456789/4800/4/7417.pdf
[2] 8.2.2 Gráficas en 3D en Python, sólidos de revolución. http://blog.espol.edu.ec/ccpg1001/graficas-en-3d-en-python-sistema-de-ecuaciones-y-planos/
[3] Volumes: Washer Method Animation 2. Stacey Roshan. 24 Abril 2016.

2023-11-222024-07-11

1Eva_2023PAOII_T3 aceleración en avión de acrobacias

1ra Evaluación 2023-2024 PAO II. 21/Noviembre/2023

Tema 3. (30 puntos) Por medio del acelerómetro o sensor de fuerzas g de un avión se acrobacias se obtienen datos cada 5 segundos.

t	0	5	10	15	20	25	30	35	40	45	50
Aceleración (G)	1	1.2	1.3	2.5	4.5	3.2	1.4	0.0	-0.9	-1.0	0.2

Para un estudio detallados de la acrobacia realizada se requiere disponer de datos cada segundo
usando interpolación polinómica con el método de Lagrange.

a. Plantear el ejercicio describiendo los criterios a usar para el o los polinomios para el eje y.

b. Desarrolle el método sobre los puntos seleccionados con las expresiones completas desarrolladas con el algoritmo.

c. Presentar el polinomio resultante y la gráfica usando la resolución requerida para el estudio.

d. Encuentre el error obtenido entre el polinomio y el o los puntos de prueba de los datos no usados para generar el polinomio.

e. Adjunte los archivos: algoritmos.py, resultados.txt y gráfica.png del polinomio.

t = [0,5,10,15,20,25,30,35,40,45,50]
G = [1,1.2,1.3,2.5,4.5,3.2,1.4,0.0,-0.9,-1.0,0.2]

Rúbrica: literal a (5 puntos), literal b (10 puntos), literal c (5 puntos), literal d (5 puntos), literal e (5 puntos).

Referencias: [1] VUELO ACROBÁTICO. TDP Club. RTVE. 30 enero 2020

[2] High intensity aerobatic flying with C.J. Wilson and Kirby Chambliss. Red Bull. 6 mar 2014.

2023-11-222023-11-29

1Eva_2023PAOII_T2 Trayectoria de buque en puerto

1ra Evaluación 2023-2024 PAO II. 21/Noviembre/2023

Tema 2. (40 puntos) El DPS (Dynamic Positioning System) controla automáticamente la posición y el rumbo de un barco usando propulsión activa mediante un ordenador y una variedad de sistemas y funciones.

En el caso de entradas a puertos comerciales de alto tráfico y limitado espacio se convierten el una herramienta indispensable para gestionar las recorridos de ingreso o salida.

Suponga que como primer paso para planificar una ruta de un barco de contenedores, minimizando el gasto de energía usando la inercia del barco se planifica una ruta siguiendo los puntos de marca indicados en la tabla.

Puntos referenciales para la ruta
x	0.1	2.0	4.0	5.0	7.0
y	1.0	8.0	0.0	-1.0	3.0

a. Plantee el ejercicio usando un polinomio de interpolación y un sistema de ecuaciones.

b. Establezca la forma matricial del sistema de ecuaciones (Vandermonde) y como matriz aumentada

c. De ser necesario realice el pivoteo parcial por filas

d. Use el método directo Gauss, desarrolle todas las expresiones de las operaciones que realiza el algoritmo numérico. Estime la tolerancia y justifique.

e. Comente sobre la convergencia del método si usara un método iterativo. (número de condición)

f. Adjunte los archivos: algoritmos.py, resultados.txt y gráfica.png del polinomio.

x = [0.1,2.0,4.0,5.0,7.0]
y = [1.0,8.0,0.0,-1.0,3.0]

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (15 puntos), literal e (5 puntos), literal f (5 puntos).

Referencia: [1] Gigante buque ingresa a las terminales portuarias de Guayaquil. El Universo. 18 Ene 2020. https://youtu.be/X5S9x53Z_mY?
[2] Reportan congestión de buques de carga en puertos de EE.UU. Noticias Telemundo. 22 sept 2021.

[3] Colisiones y errores de barcos jamás capturados en cámara. 21 oct 2023.

2023-11-222023-11-29

1Eva_2023PAOII_T1 GPR Radar penetrante de suelo

1ra Evaluación 2023-2024 PAO II. 21/Noviembre/2023

Tema 1. (30 puntos) Radar penetrante o GPR (Ground Penetrating Radar) es el término general aplicado para mapear o cartografiar estructuras enterradas en el suelo.
El GPR se utiliza en muchas áreas como la localización de tuberías enterradas para servicios públicos, la evaluación del sitio en minas, excavaciones arqueológicas, medición del espesor de nieve o hielo para la gestión de pistas de esquí, etc.
Al emitir un pulso de radio hacia el suelo, la señal rebota al cambiar de medio y puede ser detectada en la superficie. Por lo que la distancia recorrida por la señal es de dos veces d.
Simplificando el ejercicio, considere la potencia de la señal recibida en el receptor en dB se expresa como:

RSSI(d)=-10\alpha log_{10}(d)+ P_0 ; d\gt0

Suponga que el coeficiente de atenuación del medio α = 4.5, P0 = – 20 y Rssi = -90, que la composición del suelo es uniforme y no existen pérdidas al rebotar sobre el material de la tubería mostrada en la gráfica.

a. Plantear el ejercicio para encontrar la profundidad a la que se encontraría la tubería usando el método de Newton-Raphson.

b. Describa el criterio para seleccionar un valor inicial de búsqueda y la tolerancia a usar en la solución.

c. Realice al menos tres iteraciones para el método indicado.

d. Realice observaciones sobre la convergencia del método.

e. Adjunte los archivos: algoritmos.py, resultados.txt y gráfica.png

Rúbrica: literal a (5 puntos), literal b (3 puntos), literal c (12 puntos), literal d (5 puntos), literal e (5 puntos)

Referencia: [1] ¿Puedo predecir la profundidad de exploración?. Sensors&Software. https://www.sensoft.ca/es/blog/what-is-gpr/
[2] Te mostramos en realidad aumentada cómo son los túneles. Univisión Noticias. 16 oct 2023.

2023-09-132023-09-15

3Eva_2023PAOI_T4 Especies en competencia por recursos

3ra Evaluación 2023-2024 PAO I. 12/Septiembre/2023

Tema 4. (30 puntos) Considere dos especies de animales que ocupan el mismo ecosistema, en competencia por los recursos de alimentos y espacio definidas por:

\frac{dx}{dt} = x(2 - 0.4 x - 0.3 y)

\frac{dy}{dt} = y( 1 - 0.1 y - 0.3 x)

Donde las poblaciones de x(t) y y(t) se miden en miles y t en años. Use un método numérico para analizar las poblaciones en un periodo largo para el caso que: x(0)=1.5, y(0)=3.5

a. Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

b. Desarrolle tres iteraciones para x(t), y(t) con tamaño de paso h=0.5.

c. Usando el algoritmo, aproxime la solución entre t=0 a t=10 años, adjunte sus resultados en la evaluación.

d. Realice una observación sobre el crecimiento de la población de las especies y(t) a lo largo del tiempo.

Rúbrica: literal a (5 puntos), literal b (15 puntos), literal c (5 puntos), literal d (5 puntos)

Referencia: [1] Modelos de competencia ejercicio 10. Zill, Dennis G. Ecuaciones diferenciales con aplicaciones de modelado. Edición 9. P109. p111.

[2] Competition in ecosystems. Stile Education. 11 septiembre 2019.

2023-09-132023-09-15

3Eva_2023PAOI_T3 Perfil de área devastada por incendios

3ra Evaluación 2023-2024 PAO I. 12/Septiembre/2023

3Eva_2023PAOI_T2 Área devastada por incendios

Tema 3. (20 puntos) Continuando con el ejercicio del área devastada por el incendio, con el objetivo de simplificar el registro de datos se propone describir los perfiles usando polinomios.

Frontera superior

X	350	300	350	420	444	484	504	534	568	620	660	720	780	740	800	800
Y	0	315	315	315	320	336	400	415	462	510	550	550	490	390	390	150

Frontera inferior

X	350	459	666	800
Y	0	63	130	150

a. Plantear el ejercicio para realizar interpolación polinómica. Describa criterios, intervalos, método.

b. Desarrolle el o los polinomios para la frontera superior, siguiendo el método propuesto en el literal a.

c. Desarrolle el o los polinomios para la frontera inferior, con un método diferente al literal a.

d. Usando un algoritmo, graficar al menos un resultado del literal b y c.

Rúbrica: literal a (5 puntos), literal b (5 puntos), literal c (5 puntos), literal d (5 puntos)