Ejercicio: s1Eva_2024PAOII_T3 matriz de distribución de energía por sectores

:

Fuente\Consumidor	Industrial	Comercial	Transporte	Residencial
Hidroeléctrica	0.7	0.19	0.1	0.01
Gas Natural	0.12	0.18	0.68	0.02
Petróleos-combustible	0.2	0.38	0.4	0.02
Eólica	0.11	0.23	0.15	0.51

total de fuente de generación para la tabla es: [1500,400,600,200]

literal a Planteamiento

Considerando que el factor de la tabla es el factor de consumo por tipo de cliente, para encontrar las cantidades por tipo cliente que se puedan atender con la capacidad de cada "fuente de generación", se plantea:

0.7x+0.19y+0.1z+0.01w = 1500 0.12x+0.18y+0.68z+0.02w = 400 0.2x+0.38y+0.4z+0.04w = 600 0.11x+0.23y+0.15z+0.51w =200

literal b. Matriz aumentada y Pivoteo parcial por filas

\begin{bmatrix} 0.7 & 0.19& 0.1 & 0.01 &1500 \\ 0.12 & 0.18 & 0.68 & 0.02 & 400 \\0.2 & 0.38 & 0.4 & 0.02 & 600 \\0.11 & 0.23& 0.15 & 0.51 & 200 \end{bmatrix}

Revisando la primera columna j=0,  el mayor valor ya se encuentra en la posición de la diagonal i=0, por lo que no hay cambio de filas

Para la segunda columna j=1, desde la posición de la diagonal i=1, el mayor valor se encuentra en i=2, por lo que intercambian las filas.

\begin{bmatrix} 0.7 & 0.19& 0.1 & 0.01 &1500\\0.2 & 0.38 & 0.4 & 0.02 & 600 \\ 0.12 & 0.18 & 0.68 & 0.02 & 400 \\ 0.11 & 0.23& 0.15 & 0.51 & 200 \end{bmatrix}

Al observar la tercera columna j=2, desde la diagonal i=2, el valor mayor ya se encuentra en la posición de la diagonal, no hay cambio de filas. Para la última fila no se tiene otra fila para comparar, con lo que el pivoteo se terminó.

literal c. Método de Jacobi

A partir de la matriz del literal anterior, las expresiones quedan:

0.7x+0.19y+0.1z+0.01w = 1500 0.2x+0.38y+0.4z+0.04w = 600 0.12x+0.18y+0.68z+0.02w = 400 0.11x+0.23y+0.15z+0.51w =200

y despejar una incógnita de cada ecuación se convierte en:

x = \frac{1}{0.7} \Big( 1500 - (+0.19y+0.1z+0.01w) \Big) y = \frac{1}{0.38} \Big( 600 - (0.2x +0.4z+0.04w) \Big) z = \frac{1}{0.68} \Big(400-(0.12x+0.18y+0.02w)\Big) w =\frac{1}{0.51} \Big(200-(0.11x+0.23y+0.15z) \Big)

literal d. iteraciones

En el literal c, se sugiere iniciar con el vector X₀ = [100,100,100,100].

Como la unidad de medida en las incógnitas es número de clientes, la tolerancia puede ajustarse a 0.1.

itera = 0

X₀ = [100,100,100,100]

x = \frac{1}{0.7} \Big( 1500 - (+0.19(100)+0.1(100)+0.01(100)) \Big) = 2100 y = \frac{1}{0.38} \Big( 600 - (0.2(100) +0.4(100)+0.04(100)) \Big) = 1415.7 z = \frac{1}{0.68} \Big(400-(0.12(100)+0.18(100)+0.02(100))\Big) = 541.17 w =\frac{1}{0.51} \Big(200-(0.11(100)+0.23(100)+0.15(100)) \Big) =296.1 errado = max| [ 2100-100, 1415.7-100, 541.17-100, 296.1-100] | errado = max| [ 2000, 1315.7,441.17,196.1] | = 2000

itera = 1

X₀ = [ 2100, 1415.7, 541.1, 296.1 ]

x = \frac{1}{0.7} \Big( 1500 - (+0.19(1415.7)+0.1(541.1)+0.01(296.1)) \Big) = 1677.0 y = \frac{1}{0.38} \Big( 600 - (0.2(2100) +0.4(541.1)+0.04( 296.1)) \Big) = -111.55 z = \frac{1}{0.68} \Big(400-(0.12(2100)+0.18(1415.7)+0.02(541.1))\Big) = -165.82 w =\frac{1}{0.51} \Big(200-(0.11( 2100)+0.23( 1415.7)+0.15(541.1)) \Big) =-858.44 errado = max| [ 1677.0 - 2100,-111.55 -1415.7, -165.82- 541.17, -858.44- 296.1] | errado = max| [ -423, -1527.25 ,-706.99 ,-1154.54] | = 1527.25

itera = 2

tarea..

literal e. convergencia y revisión de resultados obtenidos

Para el asunto de convergencia, el error disminuye entre iteraciones, por lo que el método es convergente.

Analizando los resultados desde la segunda iteración, se obtienen valores negativos, lo que no es acorde al concepto del problema. Se continuarán con las iteraciones siguientes y se observará el resultado para dar mayor "opinión" sobre lo obtenido.

literal f Número de condición

Número de condición = 5.77 que al ser "bajo y cercano a 1" se considera que el método converge.

Resultados con el algoritmo

Iteraciones Jacobi
itera,[X],errado
0 [100. 100. 100. 100.] 1.0
1 [2100.      1415.78947  541.17647  296.07843] 2000.0
2 [1677.03081 -111.55831 -165.82893 -858.44716] 1527.3477812177503
3 [2209.09063  916.03777  347.06727  129.52816] 1027.5960799832396
4 [1842.78688   44.11685  -47.89447 -599.50735] 871.9209205662409
5 [2146.28903  691.02779  268.99219  -11.1162 ] 646.9109334007268
...
40 [2022.87519  383.13614  137.36642 -257.41944] 0.11802984805018468
41 [2022.91669  383.22837  137.41009 -257.33833] 0.09223623893257127
numero de condición: 5.7772167744910625
respuesta X: 
[2022.91669  383.22837  137.41009 -257.33833]
iterado, incluyendo X0:  42

El resultado muestra que los clientes residenciales serán -257 según las ecuaciones planteadas. Lo que se interpreta según lo presentado por los estudiantes:

1. energía insuficiente: causa por los apagones diarios en el país en éstos días.

2. Se requiere mejorar el planteamiento, pues la respuesta no debe contener valores negativos según el concepto planteado en el ejercicio.

Se considerarán ambas válidas para la evaluación al observar que el resultado numérico es correcto, pero no es acorde al ejercicio.

 

Instrucciones en Python

# 1Eva_2024PAOII_T3 matriz de distribución de energía por sectores
import numpy as np

#INGRESO
A= [[0.7,0.19,0.1,0.01],
    [0.12,0.18,0.68,0.02],
    [0.2,0.38,0.4,0.02],
    [0.11,0.23,0.15,0.51]]

B = [1500,400,600,200]

# PROCEDIMIENTO
A = np.array(A,dtype=float)
B = np.transpose([np.array(B)])

X0 = [100,100,100,100]
tolera = 0.1
iteramax = 100
verdecimal = 5

def jacobi(A,B,X0, tolera, iteramax=100, vertabla=False, precision=4):
    ''' Método de Jacobi, tolerancia, vector inicial X0
        para mostrar iteraciones: vertabla=True
    '''
    A = np.array(A,dtype=float)
    B = np.array(B,dtype=float)
    X0 = np.array(X0,dtype=float)
    tamano = np.shape(A)
    n = tamano[0]
    m = tamano[1]
    diferencia = np.ones(n, dtype=float)
    errado = np.max(diferencia)
    X = np.copy(X0)
    xnuevo = np.copy(X0)
    tabla = [np.copy(X0)]

    itera = 0
    if vertabla==True:
        print('Iteraciones Jacobi')
        print('itera,[X],errado')
        print(itera, xnuevo, errado)
        np.set_printoptions(precision)
    while not(errado<=tolera or itera>iteramax):
        
        for i in range(0,n,1):
            nuevo = B[i]
            for j in range(0,m,1):
                if (i!=j): # excepto diagonal de A
                    nuevo = nuevo-A[i,j]*X[j]
            nuevo = nuevo/A[i,i]
            xnuevo[i] = nuevo
        diferencia = np.abs(xnuevo-X)
        errado = np.max(diferencia)
        X = np.copy(xnuevo)
        
        tabla = np.concatenate((tabla,[X]),axis = 0)

        itera = itera + 1
        if vertabla==True:
            print(itera, xnuevo, errado)

    # No converge
    if (itera>iteramax):
        X=itera
        print('iteramax superado, No converge')
    return(X,tabla)

def pivoteafila(A,B,vertabla=False):
    '''
    Pivotea parcial por filas, entrega matriz aumentada AB
    Si hay ceros en diagonal es matriz singular,
    Tarea: Revisar si diagonal tiene ceros
    '''
    A = np.array(A,dtype=float)
    B = np.array(B,dtype=float)
    # Matriz aumentada
    nB = len(np.shape(B))
    if nB == 1:
        B = np.transpose([B])
    AB  = np.concatenate((A,B),axis=1)
    
    if vertabla==True:
        print('Matriz aumentada')
        print(AB)
        print('Pivoteo parcial:')
    
    # Pivoteo por filas AB
    tamano = np.shape(AB)
    n = tamano[0]
    m = tamano[1]
    
    # Para cada fila en AB
    pivoteado = 0
    for i in range(0,n-1,1):
        # columna desde diagonal i en adelante
        columna = np.abs(AB[i:,i])
        dondemax = np.argmax(columna)
        
        # dondemax no es en diagonal
        if (dondemax != 0):
            # intercambia filas
            temporal = np.copy(AB[i,:])
            AB[i,:] = AB[dondemax+i,:]
            AB[dondemax+i,:] = temporal

            pivoteado = pivoteado + 1
            if vertabla==True:
                print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax+i)
    if vertabla==True:
        if pivoteado==0:
            print('  Pivoteo por filas NO requerido')
        else:
            print('AB')
    return(AB)

# PROGRAMA Búsqueda de solucion  --------


# PROCEDIMIENTO
AB = pivoteafila(A,B,vertabla=True)
# separa matriz aumentada en A y B
[n,m] = np.shape(AB)
A = AB[:,:m-1]
B = AB[:,m-1]

[X, puntos] = jacobi(A,B,X0,tolera,vertabla=True,precision=verdecimal)
iterado = len(puntos)

# numero de condicion
ncond = np.linalg.cond(A)

# SALIDA
print('numero de condición:', ncond)
print('respuesta X: ')
print(X)
print('iterado, incluyendo X0: ', iterado)

Ejercicio: 1Eva_2024PAOII_T2 Interpolar x(t) en caída de cofia para t entre[1,2]

De la tabla del ejercicio, solo se toman las dos primeras filas ti,xi

ti	1	1.2	1.4	1.8	2
xi	-80.0108	-45.9965	3.1946	69.5413	61.1849
yi	-8.3002	-22.6765	-20.9677	15.8771	33.8999
zi	113.8356	112.2475	110.5523	106.7938	104.71

literal a. Planteamiento

En el planteamiento del problema para un polinomio de grado 3 indicado en el enunciado, se requieren al menos 4 puntos (grado=puntos-1). Al requerir cubrir todo el intervalo, los puntos en los extremos son obligatorios, quedando solo dos puntos por seleccionar, que se sugiere usar alrededor de 1.63 que es el valor buscado. quedando de ésta forma la selección de los puntos:

xi = [1. , 1.4, 1.8, 2. ]
fi = [-80.0108, 3.1946,  69.5413,  61.1849]

En el parcial, se revisaron dos métodos: polinomio de interpolación con sistema de ecuaciones en la Unidad 3, y el conceptual con diferencias divididas de Newton. Por la extensión del desarrollo se realiza con diferencias divididas de Newton, que por facilidad de espacios se muestra en dos tablas, la de operaciones y resultados.

Tabla de operaciones:

i	ti	f[ti]	Primero	Segundo	Tercero
0	1	-80.0108	\frac{3.1946-(-80.0108)}{1.4-1}	\frac{165.8667-208.0135}{1.8-1}	\frac{-346.0812-52.6834}{2-1}
1	1.4	3.1946	\frac{69.5413-3.1946}{1.8-1.4}	\frac{-41.782-165.8667}{2-1.4}
2	1.8	69.5413	\frac{61.1849-69.5413}{2-1.8}
3	2	61.1849

Tabla de resultados

i	ti	f[ti]	Primero	Segundo	Tercero
0	1	-80.0108	208.0135	-52.6834	-293.3978
1	1.4	3.1946	165.8667	-346.0812
2	1.8	69.5413	-41.782
3	2	61.1849

Se construye el polinomio con los datos de la primera fila:

p(t) = -80.0108 +208.0135 (t - 1) - 52.6834(t - 1)(t - 1.4) -293.3978(t - 1)(t - 1.4)(t - 1.8)

literal b. verificar polinomio

Se puede verificar de dos formas: probando los puntos o con la gráfica del algoritmo. La forma de escritura del polinomio hace cero algunos términos.

p(1.4) = -80.0108+208.0135 ((1.4) - 1) - 52.6834((1.4) - 1)((1.4) - 1.4) -293.3978((1.4) - 1)((1.4) - 1.4)((1.4) - 1.8) = 3.1846 p(1.8) = -80.0108+208.0135 ((1.8) - 1) - 52.6834((1.8) - 1)(t - 1.4) -293.3978((1.8) - 1)((1.8) - 1.4)((1.8) - 1.8) =69.5413

La gráfica del algoritmo muestra que el polinomio pasa por todos los puntos.

literal c. error en polinomio

El punto de la tabla que no se usó es t = 1.2, que al evaluar en el polinomio se obtiene:

p(1.2) = -80.0108+ 208.0135 ((1.2) - 1) - 52.6834((1.2) - 1)((1.2) - 1.4) -293.3978((1.2) - 1)((1.2) - 1.4)((1.2) - 1.8) = -43.3423 errado = |-43.3423 -(-45.9965)| = 2.65

literal d. conclusiones y recomendaciones

Para el error  P(1.2). dado el orden de magnitud en el intervalo podría considerarse "bajo" e imperceptible al incorporarlo en la gráfica.

literal e. error en otro punto

El polinomio evaluado en t=1.65

p(1.65) = -80.0108 + 208.0135 ((1.65) - 1) - 52.6834((1.65) - 1)((1.65) - 1.4) -293.3978((1.65) - 1)((1.65) - 1.4)((1.65) - 1.8) = 53.7884

la fórmula para x(t) del tema 1

x(t) = 15.35 - 13.42 t+100e^{-0.12t} cos(2\pi (0.5) t + \pi / 8) x(1.65) = 15.35 - 13.42(1.65)+100e^{-0.12(1.65)} cos(2\pi (0.5) (1.65) + \pi / 8) = 55.5884 errado = |55.5884 -53.7884| = 1.79

resultados del algoritmo

Tabla Diferencia Dividida
[['i   ', 'xi  ', 'fi  ', 'F[1]', 'F[2]', 'F[3]', 'F[4]']]
[[   0.        1.      -80.0108  208.0135  -52.6834 -293.3978    0.    ]
 [   1.        1.4       3.1946  165.8667 -346.0812    0.        0.    ]
 [   2.        1.8      69.5413  -41.782     0.        0.        0.    ]
 [   3.        2.       61.1849    0.        0.        0.        0.    ]]
dDividida: 
[ 208.0135  -52.6834 -293.3978    0.    ]
polinomio: 
208.0135*t - 293.3978125*(t - 1.8)*(t - 1.4)*(t - 1.0) - 52.6834375000001*(t - 1.4)*(t - 1.0) - 288.0243
polinomio simplificado: 
-293.3978125*t**3 + 1179.587375*t**2 - 1343.7817375*t + 377.581375
>>> polinomio.subs(t,1.65)
53.7884880859375
>>> 15.35 - 13.42*(1.65)+100*np.exp(-0.12*(1.65))*np.cos(2*np.pi*(0.5)*(1.65) + np.pi/8)
55.588413032442766
>>> 55.5884 -53.7884
1.7999999999999972
>>>

las gráficas se muestran en los literales anteriores

# 1Eva_2024PAOII_T2 Interpolar x(t) en caída de cofia para t entre[1,2]
# Polinomio interpolación
# Diferencias Divididas de Newton
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO , Datos de prueba
xi = [1. , 1.4, 1.8, 2. ]
fi = [-80.0108, 3.1946,  69.5413,  61.1849]

##ti = [1. , 1.2, 1.4, 1.8, 2. ]
##xi = [-80.0108, -45.9965,   3.1946,  69.5413,  61.1849]
##yi = [ -8.3002, -22.6765, -20.9677,  15.8771,  33.8999]
##zi = [113.8356, 112.2475, 110.5523, 106.7938, 104.71 ]


# PROCEDIMIENTO
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)

# Tabla de Diferencias Divididas
titulo = ['i   ','xi  ','fi  ']
n = len(xi)
ki = np.arange(0,n,1)
tabla = np.concatenate(([ki],[xi],[fi]),axis=0)
tabla = np.transpose(tabla)

# diferencias divididas vacia
dfinita = np.zeros(shape=(n,n),dtype=float)
tabla = np.concatenate((tabla,dfinita), axis=1)

# Calcula tabla, inicia en columna 3
[n,m] = np.shape(tabla)
diagonal = n-1
j = 3
while (j < m):
    # Añade título para cada columna
    titulo.append('F['+str(j-2)+']')

    # cada fila de columna
    i = 0
    paso = j-2 # inicia en 1
    while (i < diagonal):
        denominador = (xi[i+paso]-xi[i])
        numerador = tabla[i+1,j-1]-tabla[i,j-1]
        tabla[i,j] = numerador/denominador
        i = i+1
    diagonal = diagonal - 1
    j = j+1

# POLINOMIO con diferencias Divididas
# caso: puntos equidistantes en eje x
dDividida = tabla[0,3:]
n = len(dfinita)

# expresión del polinomio con Sympy
t = sym.Symbol('t')
polinomio = fi[0]
for j in range(1,n,1):
    factor = dDividida[j-1]
    termino = 1
    for k in range(0,j,1):
        termino = termino*(t-xi[k])
    polinomio = polinomio + termino*factor

# simplifica multiplicando entre (t-xi)
polisimple = polinomio.expand()

# polinomio para evaluacion numérica
px = sym.lambdify(t,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
np.set_printoptions(precision = 4)
print('Tabla Diferencia Dividida')
print([titulo])
print(tabla)
print('dDividida: ')
print(dDividida)
print('polinomio: ')
print(polinomio)
print('polinomio simplificado: ' )
print(polisimple)

# Gráfica
plt.plot(xi,fi,'o', label = 'Puntos')
plt.plot(pxi,pfi, label = 'Polinomio')

plt.xlabel('ti')
plt.ylabel('xi')
plt.grid()
plt.title('Polinomio de interpolación')

plt.plot(1.65,polinomio.subs(t,1.65),
         'o',color='red',label='p(1.65)')
plt.plot(1.2,polinomio.subs(t,1.2),
         'o',color='green',label='p(1.2)')
plt.legend()
plt.show()

 

Ejercicio: 1Eva_2024PAOII_T1 Capturar en el mar las cofias de cohetes

literal a. Planteamiento

Para encontrar el valor t cuando la cofia alcanza 30 mts o 0.030 Km se usa la fórmula del eje z(t)=0.030 dado que se indica que las fórmulas se encuentran en Km.

z(t) = 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 0.030 = 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 f(t) = - 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 = 0

literal b, Intervalo para búsqueda

En el enunciado se indica que " trayectoria de caída que no es de más de 10 minutos desde desacople del cohete."

Al considerar el inicio del "evento" desacople del cohete como t=0, el intervalo a usar es entre [0,10].

Para verificar el intervalo de búsqueda, se evalúa la función z(t) en los extremos del intervalo:

f(0) = - 0.030 + 120 + \frac{450}{60} (0) \Big(1-e^{-0.35(0)} \Big) - \frac{g}{2} (0)^2 + 0.012(7.5+25.28(0))^2 = 120.645 f(10) = - 0.030 + 120 + \frac{450}{60} (10) \Big(1-e^{-0.35(10)} \Big) - \frac{g}{2} (10)^2 + 0.012(7.5+g(10))^2 = -140.509

con lo que se muestra el cambio de signo de f(t) dentro del intervalo, que verifica el intervalo de búsqueda.

con el algoritmo:

>>> fz(0)-0.03
120.645
>>> fz(10)-0.03
-140.50972375667382
>>>

también puede verificarse usando las gráficas de las trayectorias de cada eje vs el tiempo en el intervalo. Para el eje z, se puede marcar el punto de interés al trazar una línea horizontal en cero o en la altura z(t) = 0.030.

literal c. Iteraciones

Se indica usar el método del punto fijo, donde es necesario definir g(t) como un lado de la balanza, mientra que del otro lado es la identidad con t. de la fórmula se despeja por ejemplo del término t²

\frac{g}{2} t^2 + 0.012(7.5+gt)^2 f(t) = - 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) - \frac{g}{2} t^2 + 0.012(7.5+gt)^2 = 0 \frac{g}{2} t^2 = - 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 t^2 = \frac{2}{g}\Big(- 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 \Big) t = \sqrt{\frac{2}{g} \Big(- 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 \Big)}

siendo g(t) la parte derecha de la ecuación:

g(t) = \sqrt{\frac{2}{g} \Big(- 0.030 + 120 + \frac{450}{60} t \Big(1-e^{-0.35t} \Big) + 0.012(7.5+gt)^2 \Big)}

el punto inicial t₀ se puede escoger por ejemplo la mitad del intervalo. Según se observa la gráfica.

La tolerancia puede ser de 10 cm, o 1 m, depende de la precisión a proponer.
Para la parte escrita se selecciona 1m, como las unidades se encuentran en Km: tolera = 0.001

itera = 0

t = 5

g(5) = \sqrt{\frac{2}{35.28} \Big(- 0.030 + 120 + \frac{450}{60} (5) \Big(1-e^{-0.35(5)} \Big) + 0.012(7.5+(35.28(5))^2 \Big)} g(5) = 5.28 error = |g(5)-5| = |5.28-5| = 0.28

que es mayor que la tolerancia.

itera = 0+1 = 1

itera = 1

t = 5.28

g(5.28) = \sqrt{\frac{2}{35.28} \Big(- 0.030 + 120 + \frac{450}{60} (5.28) \Big(1-e^{-0.35(5.28)} \Big) + 0.012(7.5+(35.28(5.28))^2 \Big)} g(5.28) = 5.51 error = |g(5.28)-5.28| = |5.51-5.28| = 0.23

que es mayor que la tolerancia.

itera = 1+1 = 2

itera = 2

t = 5.51

g(5.51) = \sqrt{\frac{2}{35.28} \Big(- 0.030 + 120 + \frac{450}{60} (5.51) \Big(1-e^{-0.35(5.51)} \Big) + 0.012(7.5+(35.28(5.51))^2 \Big)} g(5.51) = 5.70 error = |g(5.51)-5| = |5.70-5.51| = 0.19

que es mayor que la tolerancia.

literal d. tolerancia y error

La tolerancia se describe en la primera iteración. Por ejemplo tolera = 0.001, los errores se calculan en cada iteración.

literal e. Convergencia

El error se reduce en cada iteración, se considera que el método converge.

literal f. Respuestas con algoritmo

La respuesta de la raíz de la función se busca con el algoritmo, se requieren al menos 35 iteraciones en el método del punto fijo.

i,[a,b,tramo]
0 [5.     5.2881 0.2881]
1 [5.2881 5.5234 0.2353]
2 [5.5234 5.7176 0.1942]
3 [5.7176 5.8791 0.1615]
...
34 [6.7551e+00 6.7562e+00 1.1150e-03]
35 [6.7562e+00 6.7572e+00 9.5380e-04]
raíz en:  6.75719557313832
errado :  0.0009538025930524441
itera  :  3

la gráfica del intervalo muestra que es necesario ampliar(zoom) el eje f(x) para observar mejor.

Instrucciones en Python

# Algoritmo de punto fijo
# [a,b] son seleccionados desde la gráfica
# error = tolera

import numpy as np

# INGRESO
g = 35.28
alt =  0.030
fx = lambda t: -alt + 120 + 450/60*t*(1-np.exp(-0.35*t))-0.5*g*t**2 + 0.012*(7.5 - g*t)**2
gx = lambda t: np.sqrt((2/g)*(-alt + 120 + 450/60*t*(1-np.exp(-0.35*t)) + 0.012*(7.5 - g*t)**2))

a = 5
b = 10
tolera = 0.001 # tolera 1m, probar con 10 cm
iteramax = 100

# PROCEDIMIENTO
i = 0 # iteración
b = gx(a)
tramo = abs(b-a)

print('i,[a,b,tramo]')
np.set_printoptions(precision=4)
print(0,np.array([a,b,tramo]))

while not(tramo<=tolera or i>iteramax):
    a = b
    b = gx(a)
    tramo = abs(b-a)
    i = i + 1
    
    print(i,np.array([a,b,tramo]))

respuesta = b
# Valida convergencia
if (i>=iteramax):
    respuesta = np.nan

# SALIDA
print('raíz en: ', respuesta)
print('errado : ', tramo)
print('itera  : ', i)

# GRAFICA
import matplotlib.pyplot as plt
# calcula los puntos para fx y gx
a = 5
b = 10
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
gi = gx(xi)
yi = xi

plt.plot(xi,fi, label='f(t)',
         linestyle='dashed')
plt.plot(xi,gi, label='g(t)')
plt.plot(xi,yi, label='y=t')

plt.axvline(respuesta, color='magenta',
            linestyle='dotted')
plt.axhline(0)
plt.xlabel('t')
plt.ylabel('f(t)')
plt.title('Punto Fijo')
plt.grid()
plt.legend()
plt.show()

 

Ejercicio: 2Eva_2024PAOI_T1 EDO Salto Bungee tiempo extiende cuerda

Como referencia par el ejercicio, solo se realizará la primera parte, acorde a:

Encuentre el tiempo t_c y la velocidad de la persona cuando se alcanza la longitud de la cuerda extendida y sin estirar (30 m), es decir y<L, aún se entra cayendo signo(v)=1. (solo primera ecuación)

\frac{d^2y}{dt^2} = g - signo(v) \frac{C_d}{m}\Big( \frac{dy}{dt}\Big)^2 y \leq L

Suponga que las condiciones iniciales son:

y(0) = 0

\frac{dy(0)}{dt} = 0

literal a

Realice el planteamiento del ejercicio usando Runge-Kutta de 2do Orden

\frac{d^2y}{dt^2} = 9.8 - signo(v) \frac{0.25}{68.1}\Big( \frac{dy}{dt}\Big)^2

Usando los valores de las constantes g, C_d, m, haciendo el cambio de variable dy/dt=v. Adicionalmente, en la caída inicial, signo(v)=1 y se mantiene constante hasta el 2do tramo con la cuerda estirada.

v' = 9.8 - \frac{0.25}{68.1} v^2

Se plantea el ejercicio como Runge-Kutta para 2da derivada

v = y' = f(t,y,v) v' = g(t,y,v) = 9.8 - \frac{0.25}{68.1} v^2

siendo h=0.5, las iteraciones se realizan como:

K_{1y} = 0.5 v K_{1v} = 0.5 \Big( 9.8 - \frac{0.25}{68.1} v^2\Big) K_{2y} = 0.5 \Big( v_i + K_{1v}\Big) K_{2v} = 0.5 \Big(9.8 - \frac{0.25}{68.1}(v_i + K_{1v})^2 \Big) y_{i+1}=y_i+\frac{K_{1y}+K_{2y}}{2} v_{i+1}=v_i+\frac{K_{1v}+K_{2v}}{2} t_{i+1} = t_i +0.5

literal b

Desarrolle tres iteraciones para y(t) con tamaño de paso h=0.5

itera = 0

K_{1y} = 0.5 (0) = 0 K_{1v} = 0.5 \Big( 9.8 - \frac{0.25}{68.1} (0)^2\Big) = 4.9 K_{2y} = 0.5 ( 0 + 4.9) = 2.45 K_{2v} = 0.5 \Big(9.8 - \frac{0.25}{68.1}(0 + 2.45)^2 \Big) =4.8559 y_{i+1}=0+\frac{0+2.45}{2}=1.225 v_{i+1}=0+\frac{4.9+4.8889}{2}=4.8779 t_{i+1} =0 +0.5 = 0.5

itera=1

...

Continuar con las iteraciones como tarea.

literal c

Usando el algoritmo, aproxime la solución para y en el intervalo entre [0,t_c], adjunte sus resultados.txt

las iteraciones con el algoritmo son:

 [ ti, yi, vi,K1y,K1v,K2y,K2v]
[[0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00 0.000000e+00
  0.000000e+00 0.000000e+00]
 [5.000000e-01 1.225000e+00 4.877964e+00 0.000000e+00 4.900000e+00
  2.450000e+00 4.855929e+00]
 [1.000000e+00 4.878063e+00 9.669162e+00 2.438982e+00 4.856324e+00
  4.867144e+00 4.726071e+00]
 [1.500000e+00 1.089474e+01 1.429311e+01 4.834581e+00 4.728391e+00
  7.198776e+00 4.519513e+00]
 [2.000000e+00 1.917255e+01 1.868062e+01 7.146557e+00 4.525013e+00
  9.409063e+00 4.249997e+00]
 [2.500000e+00 2.957773e+01 2.277738e+01 9.340309e+00 4.259461e+00
  1.147004e+01 3.934054e+00]
 [3.000000e+00 4.195334e+01 2.654573e+01 1.138869e+01 3.947708e+00
  1.336254e+01 3.589005e+00]

con lo que se observa que para alcanzar los 30m de la cuerda sin estirar se alcanzan entre los [2.5, 3.0] s.

literal d

Indique el valor de t_c, muestre cómo mejorar la precisión y realice sus observaciones sobre los resultados.

Para mejorar la precisión del algoritmo se reduce el valor del tamaño de paso h,  de esta forma se puede obtener una mejor lectura del tiempo de la primera fase del ejercicio.

Por ejemplo haciendo el tamaño de paso h=0.5/4, el tiempo entre [2.5, 2.625]. que tiene un error segundos menor al valor encontrado inicialmente y se mejora la precisión.

 

Ejercicio: 1Eva_2024PAOI_T3 Tasas de natalidad de reemplazo en Ecuador

Los datos de la tabla que se requieren usar para la tabla son los años 1965, 1980, 1995 y 2010.

Promedio Hijos por mujer en Ecuador. INEC 29 Agosto 2019 [4]

tasa	7.32	4.89	3.50	2.79
año	1965	1980	1995	2010
k	0	3	6	9

literal a

Para cuatro datos o muestras el grado del polinomio que se puede plantear es 3. La ecuación se ordena siguiendo el modelo para la matriz de Vandermonde, primer coeficiente es del termino de mayor grado.

p(x) = ax^3+bx^2+cx+d

Por el orden de magnitud del eje x comparado con los valores de las constantes, se usan los valores del vector k que corresponde a los índices de la tabla. El valor del año se obtiene al hacer un cambio de escala que inicia en el año t₀ = 1965 y tamaño de paso Δx = 5 años.

el sistema de ecuaciones usando cada punto será:

p(0) = a(0)^3+b(0)^2+c(0)+d = 7.32 p(3) = a(3)^3+b(3)^2+c(3)+d = 4.89 p(6) = a(6)^3+b(6)^2+c(6)+d = 3.50 p(9) = a(9)^3+b(9)^2+c(9)+d = 2.79

literal b

El sistema de ecuaciones para la Matriz de Vandermonde D y el vector de constantes B en la forma de matriz aumentada D|B:

\left[ \begin{array}{cccc | c} (0)^3 & (0)^2 & (0) & 1 & 7.32 \\ (3)^3 & (3)^2 & (3) &1 &4.89\\ (6)^3 & (6)^2 & (6) &1 & 3.50 \\ (9)^3 & (9)^2 & (9) & 1 & 2.79 \end{array} \right]

literal c

Resolviendo el sistema de ecuaciones con el algoritmo y usando la instrucción np.linalg.solve(A,B)

>>> np.linalg.solve(A,B)
array([-2.22222222e-03,  7.77777778e-02,
       -1.02333333e+00,  7.32000000e+00])

literal d

p(x) = -0.00222 x^3 + 0.07777 x^2 - 1.0233 x + 7.32

Para el ajuste de escala de años, se usa:

año = x*5 +1965

la gráfica usando el algoritmo, muestra que el polinomio pasa por los puntos seleccionados y existe un error entre los puntos que no participan en la construcción del polinomio.

literal e

El año 2020 en x se escala como

2020 = x*5 +1965

x = 11

o revisando la tabla proporcionada en el ejercicio

p(11) = -0.00222 (11)^3 + 0.07777(11)^2 - 1.0233 (11)x + 7.32 = 2.5166

el error se calcula usando el valor medido para el año 2020

error = | 2.51- 2.35| = 0.16

literal f

p(x) = -0.00222 x^3 + 0.07777 x^2 - 1.0233 x + 7.32 = 2.51

para resolverlo se requiere usar cualquiera de los algoritmos de la unidad 2.

>>> import scipy.optimize as opt
>>> opt.bisect(px,11,30,xtol=0.001)
20.312713623046875
>>>

que corresponde al año = 20.31*5+1965 = 2066.55

Sin embargo la interpolación se usa para estimar valores dentro del intervalo de muestras. El concepto de extrapolación corresponde a otro capítulo. Sin embargo la pregunta se la considera para evaluar la comprensión de la unidad 2.

---

Algoritmo con Python

El resultado con el algoritmo se observa como

xi [0 3 6 9]
fi [7.32 4.89 3.5  2.79]
Matriz Vandermonde: 
[[  0.   0.   0.   1.]
 [ 27.   9.   3.   1.]
 [216.  36.   6.   1.]
 [729.  81.   9.   1.]]
los coeficientes del polinomio: 
[-2.22222222e-03  7.77777778e-02 
 -1.02333333e+00  7.32000000e+00]
Polinomio de interpolación: 
-0.00222222224*x**3 + 0.077777778*x**2 - 1.02333333*x + 7.32

 formato pprint
                       3                      2                            
- 0.002222222224*x  + 0.0777777778*x  - 1.023333333*x + 7.32
>>> px(11)
2.5166666666667066

Instrucciones en Python

# 1Eva_2024PAOI_T3 Tasas de natalidad en países desarrollados
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym

# INGRESO
tasa = [7.32, 6.39, 5.58, 4.89,4.31,3.85,3.50,3.26,3.03,2.79,2.54,2.35]
anio = [1965, 1970, 1975, 1980,1985,1990,1995,2000,2005,2010,2015,2020]
k    = [   0,     1,   2,    3,   4,   5,   6,   7,   8,   9,  10,  11]
cual = [0,3,6,9]
tasamin = 2.1

# PROCEDIMIENTO
fi = np.take(tasa,cual)
xi = np.take(k,cual)

# El polinomio de interpolación
# muestras = tramos+1
muestras = 25

# PROCEDIMIENTO
# Convierte a arreglos numpy 
xi = np.array(xi)
B = np.array(fi)
n = len(xi)

# Matriz Vandermonde D
D = np.zeros(shape=(n,n),dtype =float)
for i in range(0,n,1):
    for j in range(0,n,1):
        potencia = (n-1)-j # Derecha a izquierda
        D[i,j] = xi[i]**potencia

# Aplicar métodos Unidad03. Tarea
# Resuelve sistema de ecuaciones A.X=B
coeficiente = np.linalg.solve(D,B)

# Polinomio en forma simbólica
x = sym.Symbol('x')
polinomio = 0
for i in range(0,n,1):
    potencia = (n-1)-i   # Derecha a izquierda
    termino = coeficiente[i]*(x**potencia)
    polinomio = polinomio + termino

# Polinomio a forma Lambda
# para evaluación con vectores de datos xin
px = sym.lambdify(x,polinomio)

# Para graficar el polinomio en [a,b]
a = np.min(xi)
b = np.max(xi)
xin = np.linspace(a,b,muestras)
yin = px(xin)
   
# SALIDA
print('xi', xi)
print('fi',fi)
print('Matriz Vandermonde: ')
print(D)
print('los coeficientes del polinomio: ')
print(coeficiente)
print('Polinomio de interpolación: ')
print(polinomio)
print('\n formato pprint')
sym.pprint(polinomio)

# Grafica
plt.plot(anio,tasa,'o')
plt.plot(xi*5+anio[0],fi,'o',color='red', label='[xi,fi]')
plt.plot(xin*5+anio[0],yin,color='red', label='p(x)')
plt.xlabel('xi')
plt.ylabel('fi')
plt.legend()
plt.axhline(0)
plt.axhline(2.1,linestyle='-.')
plt.xlabel('anio')
plt.ylabel('tasa')
plt.title(polinomio)
plt.show()

 

Ejercicio: 1Eva_2024PAOI_T2 Temperatura en nodos de placa cuadrada

literal a

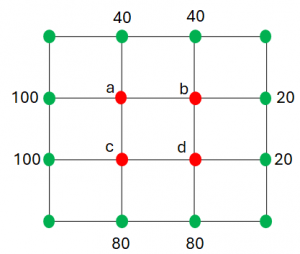
El planteamiento de las ecuaciones según se cita en la solución iterativa es el promedio de los nodos adyacentes:

 

a = \frac{100+40+b+c}{4} b = \frac{40+20+a+d}{4} c = \frac{100+80+a+d}{4} d = \frac{80+20+c+b}{4}

reordenando las ecuaciones para su forma maticial:

4a -b -c = 100+40 4b -a -d= 40+20 4c -a -d= 100+80 4d -c -b= 80+20

literal b

la forma matricial del sistema de ecuaciones es:

\begin{bmatrix} 4 & -1 &-1 & 0 \\ -1 & 4 & 0 &-1 \\ -1 & 0 & 4 &-1 \\ 0 & -1 &-1 & 4 \end{bmatrix} \begin{bmatrix} a \\ b \\ c \\ d \end{bmatrix} = \begin{bmatrix} 140 \\ 60 \\ 180 \\ 100 \end{bmatrix}

matriz aumentada:

\left[ \begin{array} {cccc|c} 4 & -1 &-1 & 0 & 140\\ -1 & 4 & 0 &-1 & 60 \\ -1 & 0 & 4 &-1 & 180 \\ 0 & -1 &-1 & 4 & 100 \end{array}\right]

al revisar el procedimiento de pivoteo parcial por filas se muestra que ya se encuentra pivoteada la matriz. Por lo que no es necesario realizar cambios en las filas.

literal c

Las expresiones a partir de la matriz aumentada y pivoteada para usar en un método iterativo como Gauss-Seidel son:

a = 0.25(b+c+140) b = 0.25*(a+d+60) c = 0.25(a+d+180) d = 0.25(c+b+100)

el vector inicial debe considerar que las temperaturas serán medias entre los  bordes de la placa

X₀ = [ (100+40)/2, (40+20)/2, (100+80)/2, (80+20)/2 ]

X₀ = [ 70, 30, 90, 50 ]

literal d iteraciones

itera = 0

a = 0.25(30+90+140)= 65

b = 0.25*(65+50+60) = 43.75

c = 0.25(65+50+180) = 73.75

d = 0.25(73.75+43.75+100) = 54.375

error = max|[65-70, 43.75-30, 73.75-90, 54.375-50]|

error = max|[ -5, 13.75, -16.25, 4.375| = 16.25

X₁ = [ 65, 43.75, 73.75, 54.375 ]

itera = 1

a = 0.25(43.75+73.75+140)= 64.375

b = 0.25*(64.375+54.375+60) = 44.687

c = 0.25(64.375+54.375+180) = 74.687

d = 0.25(74.687+44.687+100) = 54.843

error = max|[64.375-65, 44.687-43.75, 74.687-73.75, 54.843-54.375]|

error = max|[-0.625, 0.937, 0.937, 0.468| = 0.937

X₂ = [ 64.375, 44.687, 74.687, 54.843 ]

itera = 2

a = 0.25(44.687+74.687+140)= 64.843

b = 0.25*(64.843 +54.843+60) = 44.921

c = 0.25(64.843+54.843+180) = 74.921

d = 0.25(74.921+44.921+100) = 54.960

error = max|[64.843-64.375, 44.921-44.687, 74.921-74.687, 54.960-54.843]|

error = max|[0.468, 0.234, 0.234, 0.117| = 0.468

X₃ = [ 64.843, 44.921, 74.921, 54.960 ]

literal e

El método converge pues los errores en cada iteración disminuyen. Los valores obtenidos en el resultado son acorde a las temperaturas esperadas en los nodos.

Algoritmos con Python

Los resultados obtenidos son:

X 0 = [65.    43.75  73.75  54.375]
X 1 = [64.375   44.6875  74.6875  54.84375]
X 2 = [64.84375   44.921875  74.921875  54.9609375]
X 3 = [64.9609375  44.98046875 74.98046875 54.99023438]
X 4 = [64.99023438 44.99511719 74.99511719 54.99755859]
X 5 = [64.99755859 44.9987793  74.9987793  54.99938965]
X 6 = [64.99938965 44.99969482 74.99969482 54.99984741]
X 7 = [64.99984741 44.99992371 74.99992371 54.99996185]
X 8 = [64.99996185 44.99998093 74.99998093 54.99999046]
X 9 = [64.99999046 44.99999523 74.99999523 54.99999762]
respuesta X: 
[[64.99999046]
 [44.99999523]
 [74.99999523]
 [54.99999762]]
verificar A.X=B: 
[[139.99997139]
 [ 59.99999285]
 [179.99999285]
 [100.        ]]
>>>

el algoritmo usado es:

# 1Eva_2024PAOI_T2 Temperatura en nodos de placa cuadrada
# Método de Gauss-Seidel
import numpy as np
# INGRESO
A = np.array([[4,-1,-1,0],
              [-1,4,0,-1],
              [-1,0,4,-1],
              [0,-1,-1,4]],dtype=float)
B = np.array([140,60,180,100],dtype=float)
X0  = np.array([70,30,90,50],dtype=float)

tolera = 0.0001
iteramax = 100

# PROCEDIMIENTO
# Gauss-Seidel
tamano = np.shape(A)
n = tamano[0]
m = tamano[1]
#  valores iniciales
X = np.copy(X0)
diferencia = np.ones(n, dtype=float)
errado = 2*tolera

itera = 0
while not(errado<=tolera or itera>iteramax):
    # por fila
    for i in range(0,n,1):
        # por columna
        suma = 0 
        for j in range(0,m,1):
            # excepto diagonal de A
            if (i!=j): 
                suma = suma-A[i,j]*X[j]
        nuevo = (B[i]+suma)/A[i,i]
        diferencia[i] = np.abs(nuevo-X[i])
        X[i] = nuevo
    print('X',itera,'=',X)
    errado = np.max(diferencia)
    itera = itera + 1

# Respuesta X en columna
X = np.transpose([X])
# revisa si NO converge
if (itera>iteramax):
    X=0
# revisa respuesta
verifica = np.dot(A,X)

# SALIDA
print('respuesta X: ')
print(X)
print('verificar A.X=B: ')
print(verifica)

 

Ejercicio: 1Eva_2024PAOI_T1 Vaciado de reservorio semiesférico

literal a. Planteamiento

A partir de la solución expresión propuesta y simplificada del ejercicio, se reemplaza los valores de R, K, a y g que son constantes. Como se da el valor de t=(15 min)(60 s/min), se unifica la unidad de medida de tiempo a segundos pues g=9.6 m/s².

---

-\frac{4}{3}R h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{Ka}{\pi} t \sqrt{2g}

---

-\frac{4}{3}(3) h^{3/2} + \frac{2}{5} h^{5/2} = -\frac{(0.85)(0.01)}{\pi} (15)(60) \sqrt{2(9.8)}

la función para encontrar la raíz se reordena como f(h)=0

f(h) = -\frac{4}{3}(3) h^{3/2} + \frac{2}{5} h^{5/2} +\frac{(0.85)(0.01)}{\pi} (15)(60) \sqrt{2(9.8)} f(h) = -4h^{3/2} + 0.4 h^{5/2} +10.7805

Usando la gráfica proporcionada del reservorio semiesférico, el valor de h no puede superar la altura R. Al vaciar el reservorio h=0.

Por lo que el intervalo a usar es [0,3]. Se verifica la existencia de una raíz al con la gráfica y Python.

b. Método de Newton Raphson

El método requiere la derivada f'(h)

f(h) = -4h^{3/2} + 0.4 h^{5/2} +10.7805 f'(h) = -6\frac{ h^{3/2}}{h} + \frac{h^{5/2}}{h} f'(h) = -6 h^{1/2}+ h^{3/2}

El valor inicial puede ser por ejemplo, el centro del intervalo:

x_0= \frac{a+b}{2} = \frac{0+3}{2} = 1.5

itera=0

f(1.5) = -4(1.5)^{3/2} + 0.4 (1.5)^{5/2} +10.7805= 4.5343 f'(1.5) = -6\frac{ 1.5^{3/2}}{1.5} + \frac{1.5^{5/2}}{1.5} = -5.5113 x_1= x_0 - \frac{f(1.5)}{f'(1.5)}= 1.5-\frac{4.5343}{-5.5113} =2.3227 error_1 =|x1-x0| = |2.3227-1.5| =0.8227

itera=1

f(2.3227) = -4(2.3227)^{3/2} + 0.4 (2.3227)^{5/2} +10.7805= -0.09019 f'(2.3227) = -6\frac{ 2.3227^{3/2}}{2.3227} + \frac{2.3227^{5/2}}{2.3227} = -5.6043 x_2= 2.3227-\frac{-0.09019}{-5.6043} = 2.3066 error_2 = |2.3066-2.3227| =0.01611

itera=2

f(2.3227) = -4(2.3066)^{3/2} + 0.4 (2.3066)^{5/2} +10.7805= -0.0007104 f'(2.3227) = -6\frac{ 2.3227^{3/2}}{2.3227} + \frac{2.3227^{5/2}}{2.3227} = -5.6093 x_3= 2.3227-\frac{-0.0007104}{-5.6093} = 2.3066 error_3 = |2.3066-2.3066| =0.000007241

literal c, convergencia

considerando tolerancia de 10-3 (milimétrica), solo serán necesarias 3 iteraciones.

El método converge al mostrarse que los errores disminuyen en cada iteración.

El resultado se encuentra dentro del intervalo y es x = 2.3066

Algoritmo con Python

resultados:

fh:
         ____          ____                   
        /  3          /  5                    
- 4.0*\/  h   + 0.4*\/  h   + 10.7805172327811
dfh:
         ____          ____
        /  3          /  5 
  6.0*\/  h     1.0*\/  h  
- ----------- + -----------
       h             h     
['xi', 'xnuevo', 'tramo']
[[1.5000e+00 2.3227e+00 8.2272e-01]
 [2.3227e+00 2.3066e+00 1.6118e-02]
 [2.3066e+00 2.3066e+00 7.2412e-06]]
raiz en:  2.306612665792577
con error de:  7.241218404896443e-06

>>> f(1.5)
4.534318388683996
>>> df(1.5)
-5.5113519212621505
>>> f(2.3227)
-0.09019959114247378
>>> df(2.3227)
-5.604354799446854
>>> f(2.3066)
7.104683901282272e-05
>>> df(2.3066)
-5.609349350102558

instrucciones:

# 1Eva_2024PAOI_T1 Vaciado de reservorio semiesférico
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym

# INGRESO
h = sym.Symbol('h')
t = 15*60
R = 3 
g = 9.8 
area = 0.01
K = 0.85 
fh = -(4/3)*R*sym.sqrt(h**3)+(2/5)*sym.sqrt(h**5)+(K*area/np.pi)*np.sqrt(2*g)*(t)

# Grafica de f(h)
a = 0
b = 3
muestras = 15

# PROCEDIMIENTO
hi = np.linspace(a,b,muestras)
# para evaluación numérica con numpy
f = sym.lambdify(h,fh)
fi = f(hi)

# derivada con sympy
dfh = sym.diff(fh,h,1)
df = sym.lambdify(h,dfh)

# SALIDA
print('fh:')
sym.pprint(fh)
print('dfh:')
sym.pprint(dfh)

plt.plot(hi,fi)
plt.axhline(0, color='black')
plt.xlabel('h')
plt.ylabel('f')
plt.title(fh)
plt.show()

## Método de Newton-Raphson

# INGRESO
fx  = f
dfx = df
x0 = (a+b)/2 # mitad del intervalo (ejemplo)
tolera = 0.001

# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# SALIDA
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)

 

Ejercicio: 3Eva_2023PAOII_T3 Volumen por solido de revolución de un peón

El volumen se calcula a partir de la expresión:

V = \int_{a}^{b} \pi (f(x))^2 dx

xi=[ 0, 3, 5.  , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60]
yi=[15,15,13.25,14.1552, 9.6768,  9.67,  4.64,  4.64,  8.9768, 0.]

Para el intervalo [0,3]

La función es una constante

literal a, b y c

f(x) = 15 V = \int_{0}^{3} \pi (15)^2 dx = \pi (15)^2 x \big|_{0}^{3} = \pi (15)^2 (3-0) = 2120.5750

Para el intervalo [3,5]

literal a

La función es una recta con pendiente negativa

f(x) = -0.875 x + 17.625 V = \int_{3}^{5} \pi (f(x))^2 dx V = \int_{3}^{5} \pi (-0.875 x+17.625)^2 dx

para el integral con cuadratura de Gauss

g(x) = \pi (-0.875*x+17.625)^2

literal b y c

x_a = \frac{5+3}{2} - \frac{5-3}{2}\frac{1}{\sqrt{3}} = 3.4226 x_b = \frac{5+3}{2} + \frac{5-3}{2}\frac{1}{\sqrt{3}} = 4.5773

con lo que el resultado aproximado del integral se convierte en:

I \cong \frac{5-3}{2}(g(3.4226) + g(4.5773)) = \frac{5-3}{2} (672.43+582.76) = 1255.1971

Para el intervalo [5, 14.97]

literal a

Del polinomio obtenido en el ejercicio anterior para éste intervalo

f(x) = -0.1083 x^2+1.8047 x + 6.9341 V = \int_{5}^{14.97} \pi (f(x))^2 dx V = \int_{5}^{14.97} \pi (-0.1083 x^2+1.8047 x + 6.9341)^2 dx [ g(x) = \pi (-0.1083 x^2+1.8047 x + 6.9341)^2

literal b y c

x_a = \frac{14.97+5}{2} - \frac{14.97-5}{2}\frac{1}{\sqrt{3}} = 7.1069 x_b = \frac{14.97+5}{2} + \frac{14.97-5}{2}\frac{1}{\sqrt{3}} = 12.8630

con lo que el resultado aproximado del integral se convierte en:

I \cong \frac{14.97-5}{2}(g(7.1069) + g(12.8630)) = \frac{14.97-5}{2} (641.5176+469.8124) = 5539.9805

literal d

El volumen total es la suma de los resultados de cada una de las secciones:

V_{total} = 2120.5750 + 1255.1971 + 5539.9805 + ...

Tarea: continuar con los otros intervalos para obtener el volumen total.

literal e

Resultados con el algoritmo

para f(x):
[xa,xb]= [0.6339745962155612, 2.366025403784439]
[f(xa),f(xb)]= [915.4418590078262, 760.106947830205]
Volumenfx:  2513.323210257047

para f(x):
[xa,xb]= [3.4226497308103743, 4.577350269189626]
[f(xa),f(xb)]= [672.4334354361756, 582.7637293668464]
Volumenfx:  1255.1971648030221

para f(x):
[xa,xb]= [7.106908908089714, 12.863091091910285]
[f(xa),f(xb)]= [641.5176069162055, 469.8124936184865]
Volumenfx:  5539.98055116544

Instrucciones en Python

# 3Eva_2023PAOII_T3 Volumen por solido de revolución de un peón
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import axes3d

# INGRESO
# intervalos eje x, funciones
#a=0 ; b=3 ; f = lambda x: np.pi*(15)**2 + 0*x
#a=3 ; b=5 ; f = lambda x: np.pi*(-0.875*x+17.625)**2
# con el polinomio del tema 2
a=5 ; b=14.97 ; f = lambda x: np.pi*(-0.1083*x**2+1.8047*x + 6.9341)**2
# con el circulo del tema 1
#a=5 ; b=14.97 ; f = lambda x: np.pi*(np.sqrt(6.7**2-(x-8.6)**2) + 7.6)**2

xmuestras = 31

# PROCEDIMIENTO
# Volumen para f(x) con Cuadratura de Gauss
xa = (b+a)/2 + (b-a)/2*(-1/np.sqrt(3)) 
xb = (b+a)/2 + (b-a)/2*(1/np.sqrt(3))
Volumenfx = (b-a)/2*(f(xa)+f(xb))
xab = [xa,xb]
fab = [f(xa),f(xb)]

# SALIDA
print("para f(x):")
print("[xa,xb]=", xab)
print("[f(xa),f(xb)]=", fab)
print("Volumenfx: ",Volumenfx)
print()

Añadir para graficar en 2D

# grafica 2D para el area de corte en eje y,x --------
# muestras en x
xi = np.linspace(a, b, xmuestras)
fi = f(xi)
f0 = np.zeros(xmuestras,dtype=float)

# grafica 2D
figura2D = plt.figure()
grafica2D = figura2D.add_subplot(111)
grafica2D.plot(xi,fi,color='blue',label='f(x)')
grafica2D.fill_between(xi,fi,f0,color='lightblue')
grafica2D.grid()
grafica2D.set_title('Area para sólido de revolución')
grafica2D.set_xlabel('x')
grafica2D.set_ylabel('f(x)')

Añadir para graficar en 3D

# Para grafica 3D -----------------------
# angulo w de rotación
w_a = 0
w_b = 2*np.pi
w_muestras = 31

# grafica 3D muestras en x y angulo w
wi = np.linspace(w_a, w_b, w_muestras)
X, W = np.meshgrid(xi, wi)
# proyeccion en cada eje 
Yf = f(xi)*np.cos(W)
Zf = f(xi)*np.sin(W)

# grafica 3D
figura3D = plt.figure()
grafica = figura3D.add_subplot(111, projection='3d')

grafica.plot_surface(X, Yf, Zf,
color='blue', label='f(x)',
alpha=0.6, rstride=6, cstride=12)

grafica.set_title('Sólido de revolución')
grafica.set_xlabel('x')
grafica.set_ylabel('y')
grafica.set_zlabel('z')
# grafica.legend()
eleva = 30
rota = -45
deltaw = 5
grafica.view_init(eleva, rota)

# rotacion de ejes
for angulo in range(rota, 360+rota, deltaw ):
grafica.view_init(eleva, angulo)
plt.draw()
plt.pause(.001)
plt.show()

.

Ejercicio: 3Eva_2023PAOII_T2 perfil de un peón

literal a y b

Para el planteamiento de los polinomios, es necesario observar la gráfica proporcionada para el ejercicio y la correspondiente tabla de datos:

xi	0	3	5	9.985	14.97	17.97	40.04	43.29	51.6456	60
yi	15	15	13.25	14.155	9.676	9.676	4.64	4.64	8.976	0

Para el intervalo [0,3], El perfil se describe con una constante, por lo tanto:

p_1(x) = 15

Para el intervalo [3,5] el perfil se describe como una recta con pendiente negativa.

p_2(x) =a_0 + a_1 x a_1 = \frac{ 13.25-15}{5-3} = -0.875 p_2(5) = 13.25 =a_0 -0.875 (5) a_0 = 13.25 +0.875 (5) = 17.625 p_2(x) = -0.875 x + 17.625

Para el con los puntos xi = [5, 9.985, 14.97] el perfil se describe con tres puntos, por lo que el polinomio de interpolación puede ser de grado 2. Usando el método de Lagrange:

p_3(x) =\frac{(x-9.985)( x-14.97)}{(5-9.985)( 5-14.97)} 13.25 + +\frac{(x-5)( x-14.97)}{(9.985-5)( 9.985-14.97)} 14.155 + +\frac{(x-5)( x-9.985)}{(14.97-5)( 14.97-9.985)} 9.676 +

simplificando la expresión con Python y Sympy:

P_3(x) = -0.1083 x^2 + 1.8047 x + 6.9341

literal c

El error para los polinomios acorde a la gráfica proporcionada es cero para los tramos [0,3] y [3,5], dado que el primero es una constante y el segundo es una recta con pendiente.

El error de mayor magnitud se presenta con la interpolación entre el círculo de la ecuación del tema 1 y el polinomio de grado 2 en el intervalo [5, 14.97]. Tomando como ejemplo el punto intermedio del tramo derecho en:

x_k = \frac{14.97-5}{4} + 9.985= 12.4775 p_3(12.4775) = -0.1083(12.4775)^2 + 1.8047(12.4775) + 6.9341 = 12.5889 f(12.4775) = \sqrt{6.7^2-(12.4775-8.6)^2} + 7.6 = 13.0639 errado = |p_3(12.4775) - f(12.4775)| = 0.4750

literal d

Se puede mejorar la aproximación del polinomio aumentando el grado y número de puntos a usar dentro del intervalo. El resultado se debería acercar mas al perfil superior del círculo de referencia del tema 1.

Resultados para el intervalo [5, 14.97]

    valores de fi:  [13.25   14.1552  9.6768]
divisores en L(i):  [ 49.70045  -24.850225  49.70045 ]

Polinomio de Lagrange, expresiones
0.266597183727713*(x - 14.97)*(x - 9.985) 
- 0.569620596996607*(x - 14.97)*(x - 5.0) 
+ 0.194702462452553*(x - 9.985)*(x - 5.0)

Polinomio de Lagrange: 
-0.108320950816341*x**2 + 1.80477420224566*x + 6.93415275918024

Instrucciones Python

# 3Eva_2023PAOII_T2 perfil de un peón
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
xj=[ 0, 3, 5.  , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60]
yj=[15,15,13.25,14.1552, 9.6768,  9.67,  4.64,  4.64,  8.9768, 0.]


#  Datos de prueba
ia = 2
ib = 4+1
xi = np.array(xj[ia:ib])
fi = np.array(yj[ia:ib])

g = lambda x: np.sqrt(6.7**2-(x-8.6)**2) + 7.6
muestras = 21

# PROCEDIMIENTO
# Polinomio de Lagrange
n = len(xi)
x = sym.Symbol('x')
polinomio = 0
divisorL = np.zeros(n, dtype = float)
for i in range(0,n,1):
    
    # Termino de Lagrange
    numerador = 1
    denominador = 1
    for j  in range(0,n,1):
        if (j!=i):
            numerador = numerador*(x-xi[j])
            denominador = denominador*(xi[i]-xi[j])
    terminoLi = numerador/denominador

    polinomio = polinomio + terminoLi*fi[i]
    divisorL[i] = denominador

# simplifica el polinomio
polisimple = polinomio.expand()

# para evaluación numérica
px = sym.lambdify(x,polisimple)

# Puntos para la gráfica
muestras = 101
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)
gi = g(pxi)

# SALIDA
print('    valores de fi: ',fi)
print('divisores en L(i): ',divisorL)
print()
print('Polinomio de Lagrange, expresiones')
print(polinomio)
print()
print('Polinomio de Lagrange: ')
print(polisimple)

# Gráfica
plt.plot(xi,fi,'o', label = 'Puntos')
plt.plot(pxi,pfi, label = 'Polinomio')
plt.plot(pxi,gi, label = 'g(x)')
plt.legend()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Interpolación Lagrange')
plt.grid()
plt.show()

 

Ejercicio: 3Eva_2023PAOII_T1 Intersección con círculo
Encuentre las raíces de las ecuaciones simultaneas siguientes:

literal a y b

Use el enfoque gráfico para obtener los valores iniciales.

2y+1.75 x = 35.25 (y-7.6)^2 + (x-8.6)^2 = (6.7)^2

se despeja la variable dependiente de cada ecuación, para la primera:

f(x) = y = \frac{35.25}{2} - \frac{1.75}{2} x

para la segunda:

(y-7.6)^2 = (6.7)^2 - (x-8.6)^2 g(x) = y = \sqrt{(6.7)^2 - (x-8.6)^2} + 7.6

Al buscar la intersección entre f(x) y g(x) se puede encontrar con la raiz de:

distancia(x) = f(x) - g(x) distancia(x) = \Big( \frac{35.25}{2} - \frac{1.75}{2} x\Big) - \Big(\sqrt{(6.7)^2 - (x-8.6)^2} + 7.6\Big)

La primera ecuación es una recta, por lo que no aporta a las cotas de la gráfica.

La segunda ecuación es la general de un círculo centrado en (7.6, 8.6) y radio 6.7, por lo que se considera el intervalo para la gráfica entre:

[7.6 -6.7, 7.6+6.7] [0.9, 14.3]

Con lo que se puede formar la gráfica de la parte superior del círculo en Python:

Instrucciones en Python

# 3Eva_2023PAOII_T1 Intersección con círculo
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
f = lambda x: -(1.75/2)*x + (35.25/2)
g = lambda x: np.sqrt(6.7**2-(x-8.6)**2) + 7.6
distancia = lambda x: f(x)- g(x)

a = 0.5
b = 16
muestras = 21

# PROCEDIMIENTO
# literal a y b
xi = np.linspace(a,b,muestras)
fi = f(xi)
gi = g(xi)
dist_i = distancia(xi)

# SALIDA - Grafica
# literal a y b
plt.plot(xi,fi, label='f(x)')
plt.plot(xi,gi, label='g(x)')
plt.plot(xi,dist_i, label='f(x)-g(x)')
plt.axhline(0, color='black', linestyle='dashed')
plt.axvline(5, color='red', linestyle='dashed')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()

literal c

Un punto inicial de búsqueda dentro del intervalo puede ser x0=3.

Para Newton-Raphson se usa:

f(x) = \Big( \frac{35.25}{2} - \frac{1.75}{2} x\Big) - \Big(\sqrt{(6.7)^2 - (x-8.6)^2} + 7.6\Big) \frac{d}{dx}f(x) = -\frac{8.6(0.1162-0.0135x)}{\sqrt{0.0609-(0.1162x-1)^2}}-0.875

(derivada obtenida con sympy)

itera = 0 ; xi = 3

f(3) = \Big( \frac{35.25}{2} - \frac{1.75}{2} (3)\Big) - \Big(\sqrt{(6.7)^2 - ((3)-8.6)^2} + 7.6\Big) \frac{d}{dx}f(3) = -\frac{8.6(0.1162-0.0135(3))}{\sqrt{0.0609-(0.1162(3)-1)^2}}-0.875 x_1 = x_0 - \frac{f(3)}{\frac{d}{dx}f(3)} = 4.55 tramo = |4.55-3| = 1.55

itera = 1 ; xi = 4.55

f(3) = \Big( \frac{35.25}{2} - \frac{1.75}{2} (4.55)\Big) - \Big(\sqrt{(6.7)^2 - ((4.55)-8.6)^2} + 7.6\Big) \frac{d}{dx}f(3) = -\frac{8.6(0.1162-0.0135(4.55))}{\sqrt{0.0609-(0.1162(4.55)-1)^2}}-0.875 x_2 = x_1 - \frac{f(4.55)}{\frac{d}{dx}f(4.55)} = 4.98 tramo = |4.98-4.55| = 0.43

itera = 2 ; xi = 4.98

f(3) = \Big( \frac{35.25}{2} - \frac{1.75}{2} (4.98)\Big) - \Big(\sqrt{(6.7)^2 - ((4.98)-8.6)^2} + 7.6\Big) \frac{d}{dx}f(3) = -\frac{8.6(0.1162-0.0135(4.98))}{\sqrt{0.0609-(0.1162(4.98)-1)^2}}-0.875 x_3 = x_2 - \frac{f(4.98)}{\frac{d}{dx}f(4.98)} = 4.99 tramo = |4.99-4.98| = 0.01

literal d

El error disminuye en cada iteración, por lo que el método converge.

Con el algoritmo se muestra que converge a x=5

dfg(x) = 
     8.6*(0.116279069767442 - 0.0135208220659816*x)          
- --------------------------------------------------- - 0.875
     ________________________________________________        
    /                                              2         
  \/  0.606949702541915 - (0.116279069767442*x - 1)          

['xi', 'xnuevo', 'tramo']
[[3.0000e+00 4.5524e+00 1.5524e+00]
 [4.5524e+00 4.9825e+00 4.3018e-01]
 [4.9825e+00 4.9995e+00 1.6999e-02]
 [4.9995e+00 4.9996e+00 2.3865e-05]]
raiz en:  4.9995611025201585
con error de:  2.3865455016647275e-05

Instrucciones en Python

# 3Eva_2023PAOII_T1 Intersección con círculo
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# forma algebraica con sympy
x = sym.Symbol('x')
f = -(1.75/2)*x + (35.25/2)
g = sym.sqrt(6.7**2-(x-8.6)**2) + 7.6
distancia = f - g

x0 = 3
tolera = 0.0001 # 1e-4

# PROCEDIMIENTO
# literal c
dfg = sym.diff(distancia,x)
# convierte a forma numerica con numpy
# Newton-Raphson
fx = sym.lambdify(x,distancia)
dfx = sym.lambdify(x,dfg)

tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# SALIDA
print('dfg(x) = ')
sym.pprint(dfg)
print()
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)