[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
1. Ecuaciones diferenciales ordinarias aproximadas con Taylor
Referencia: Rodríguez 9.1.1 ejemplo p335. Chapra 25.1.3 p731
En los métodos con Taylor para Ecuaciones Diferenciales Ordinarias (EDO) se aproxima el resultado a n términos de la serie, para lo cual se ajusta la expresión del problema a cada derivada correspondiente.
La solución empieza usando la Serie de Taylor para tres términos ajustada a la variable del ejercicio:
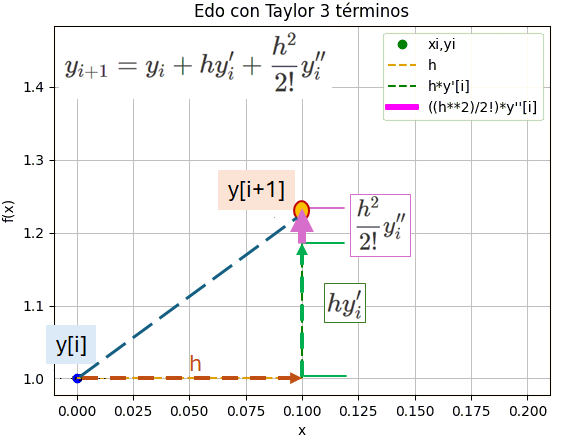
y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i x_{i+1} = x_{i} + h E = \frac{h^3}{3!} y'''(z) = O(h^3)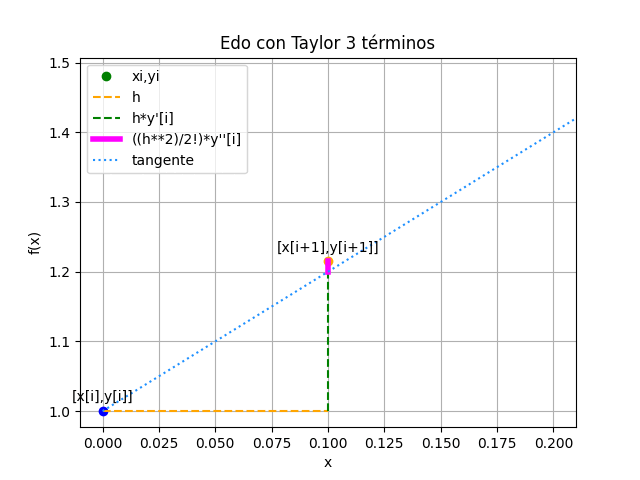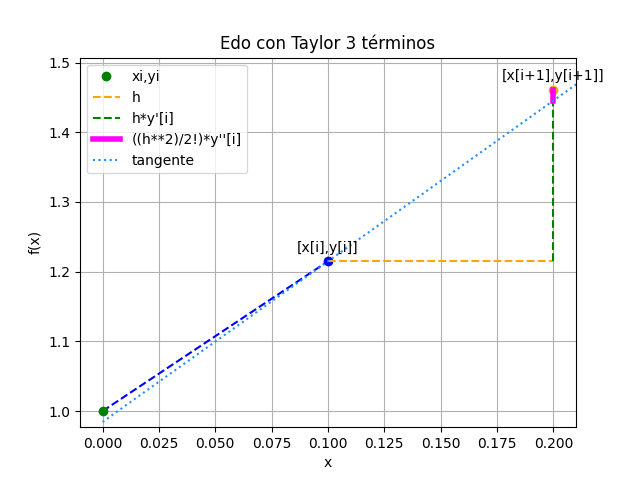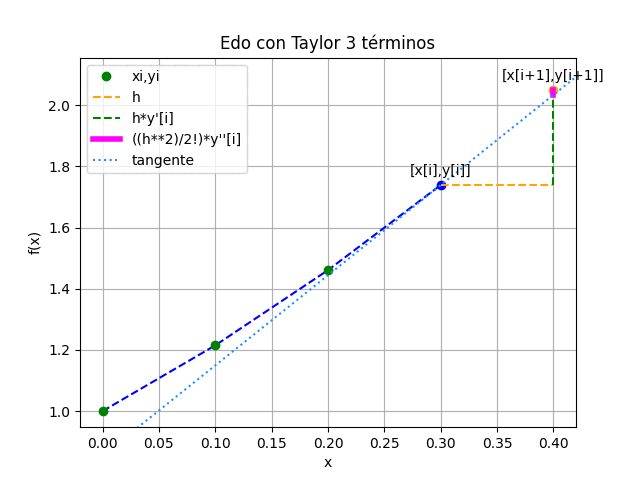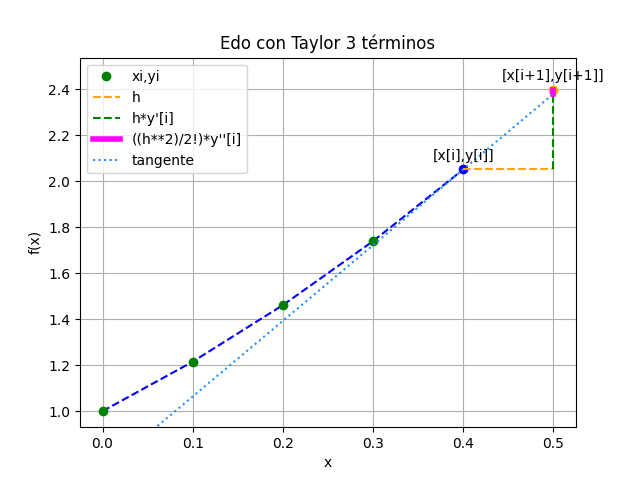
A partir de la expresión de y'(x) y el punto inicial conocido en x[i],se busca obtener el próximo valor en x[i+1] al avanzar un tamaño de paso h. Se repite el proceso en el siguiente punto encontrado y se continua hasta alcanzar el intervalo objetivo.
En éstos métodos la solución siempre es una tabla de puntos xi,yi que se pueden usar para interpolar y obtener una función polinómica.
[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
2. Ejercicio
Referencia: Rodríguez 9.1.1 ejemplo p335. Chapra 25.1.3 p731
Se requiere encontrar puntos de la solución en la ecuación diferencial usando los tres primeros términos de la serie de Taylor con h=0.1 y punto inicial x0=0, y0=1
\frac{dy}{dx}-y -x +x^2 -1 = 0que con nomenclatura simplificada:
y'-y -x +x^2 -1 = 0[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
3. Desarrollo Analítico
Al despejar el valor de y’ de expresión del ejercicio,
y' = y -x^2 +x +1se puede obtener y" al derivar una vez,
para luego combinar las expresiones en
y'' = (y -x^2 +x +1) -2x + 1simplificando:
y'' = y -x^2 -x +2Ecuaciones que permiten estimar nuevos valores yi+1 para nuevos puntos muestra distanciados en i*h desde el punto inicial siguiendo las siguientes expresiones de iteración:
y'_i = y_i -x_i^2 + x_i +1 y''_i = y_i -x_i^2 - x_i +2 y_{i+1} = y_{i} + h y'_i + \frac{h^2}{2!} y''_i x_{i+1} = x_{i} + hSe empieza evaluando el nuevo punto a una distancia x1= x0+h del punto de origen con lo que se obtiene y1 , repitiendo el proceso para el siguiente punto en forma sucesiva.
itera = 0 , x0 = 0, y0 = 1
y'_0 = 1 -0^2 +0 +1 = 2 y''_0 = 1 -0^2 -0 +2 = 3 y_1 = y_{0} + h y'_0 + \frac{h^2}{2!} y''_0 y_1 = 1 + 0.1 (2) + \frac{0.1^2}{2!} 3 = 1.215 x_1 = 0 + 0.1itera = 1 , x = 0.1, y = 1.215
y'_1 = 1.215 - 0.1^2 + 0.1 +1 = 2.305 y''_1 = 1.215 - 0.1^2 - 0.1 +2 = 3.105 y_2 = 1.215 + 0.1 (2.305) + \frac{0.1^2}{2!} 3.105 = 1.461 x_2 = 0.1 + 0.1 = 0.2itera = 2 , x = 0.2, y = 1.461
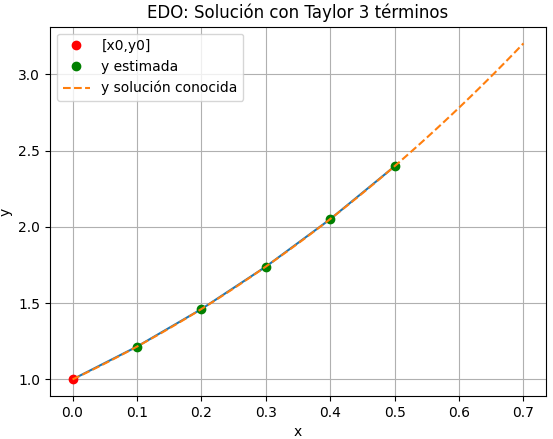
y'_2 = 1.461 - 0.2^2 + 0.2 +1 = 2.621 y''_2 = 1.461 - 0.2^2 - 0.2 +2 = 3.221 y_3 = 1.461 + 0.1 (2.621) + \frac{0.1^2}{2!} 3.221 = 1.7392 x_3 = 0.2 + 0.1 = 0.3completando los puntos con el algoritmo y realizando la gráfica se obtiene
EDO con Taylor 3 términos [xi, yi, d1yi, d2yi] [[0. 1. 0. 0. ] [0.1 1.215 2. 3. ] [0.2 1.461025 2.305 3.105 ] [0.3 1.73923262 2.621025 3.221025 ] [0.4 2.05090205 2.94923262 3.34923262] [0.5 2.39744677 3.29090205 3.49090205]] >>>
Observación, note que los resultados de las derivadas, se encuentran desplazados una fila para cada iteración. Asunto a ser considerado en la gráfica de las derivadas en caso de incluirlas.
Nota: Compare luego los pasos del algoritmo con el método de Runge-Kutta de 2do orden.
[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
..
4. Algoritmo en Python
Para simplificar los cálculos se crea una función edo_taylor3t() para encontrar los valores para una cantidad de muestras distanciadas entre si h veces del punto inicial [x0,y0]
# EDO. Método de Taylor con3 términos # estima solucion para muestras separadas h en eje x # valores iniciales x0,y0 import numpy as np def edo_taylor3t(d1y,d2y,x0,y0,h,muestras): ''' solucion a EDO usando tres términos de Taylor, x0,y0 son valores iniciales muestras es la cantidad de puntos a calcular con tamaño de paso h. ''' tamano = muestras + 1 tabla = np.zeros(shape=(tamano,4),dtype=float) # incluye el punto [x0,y0] tabla[0] = [x0,y0,0,0] x = x0 y = y0 for i in range(1,tamano,1): d1yi = d1y(x,y) d2yi = d2y(x,y) y = y + h*d1yi + ((h**2)/2)*d2yi x = x + h tabla[i] = [x,y,d1yi,d2yi] return(tabla) # PROGRAMA PRUEBA ----------------- # Ref Rodriguez 9.1.1 p335 ejemplo. # prueba y'-y-x+(x**2)-1 =0, y(0)=1 # INGRESO. # d1y = y', d2y = y'' d1y = lambda x,y: y - x**2 + x + 1 d2y = lambda x,y: y - x**2 - x + 2 x0 = 0 y0 = 1 h = 0.1 muestras = 5 # PROCEDIMIENTO tabla = edo_taylor3t(d1y,d2y,x0,y0,h,muestras) xi = tabla[:,0] yi = tabla[:,1] # SALIDA print(' EDO con Taylor 3 términos') print('[xi, yi, d1yi, d2yi]') print(tabla) # Gráfica import matplotlib.pyplot as plt plt.plot(xi,yi) plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]') plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada') plt.title('EDO: Solución con Taylor 3 términos') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid() plt.show() # plt.show() #comentar para la siguiente gráfica
Tarea: Realizar el ejercicio con más puntos muestra, donde se visualice que el error aumenta al aumentar la distancia del punto inicial [x0,y0]
[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]
5. Cálculo de Error con la solución conocida
La ecuación diferencial ordinaria del ejercicio tiene una solución conocida, lo que permite encontrar el error real en cada punto respecto a la aproximación estimada.
y = e^x + x + x^2Note que el error crece al distanciarse del punto inicial
Para las siguientes instrucciones, comente la última línea #plt.show() antes de continuar con:
# ERROR vs solución conocida y_sol = lambda x: ((np.e)**x) + x + x**2 yi_psol = y_sol(xi) errores = yi_psol - yi errormax = np.max(np.abs(errores)) # SALIDA print('Error máximo estimado: ',errormax) print('entre puntos: ') print(errores) # GRAFICA [a,b+2*h] a = x0 b = h*muestras+2*h muestreo = 10*muestras+2 xis = np.linspace(a,b,muestreo) yis = y_sol(xis) plt.plot(xis,yis,linestyle='dashed', label='y solución conocida') plt.legend() plt.show()
Se puede observar los siguientes resultados:
Error máximo estimado: 0.0012745047595 entre puntos: [ 0. 0.000170 0.000377 0.000626 0.000922 0.00127 ]
[ EDO Taylor ] [ Ejercicio ] [ Analítico ] [ Algoritmo ]