EDP Parabólica [ concepto ] Método [ explícito ] [ implícito ]
..
1. EDP Parabólicas
Referencia: Chapra 30.2 p.888 pdf.912, Burden 9Ed p714, Rodríguez 10.2 p406
Las Ecuaciones Diferenciales Parciales tipo parabólicas, semejantes a la mostrada, representa la ecuación de calor para una barra aislada sometida a fuentes de calor en cada extremo.
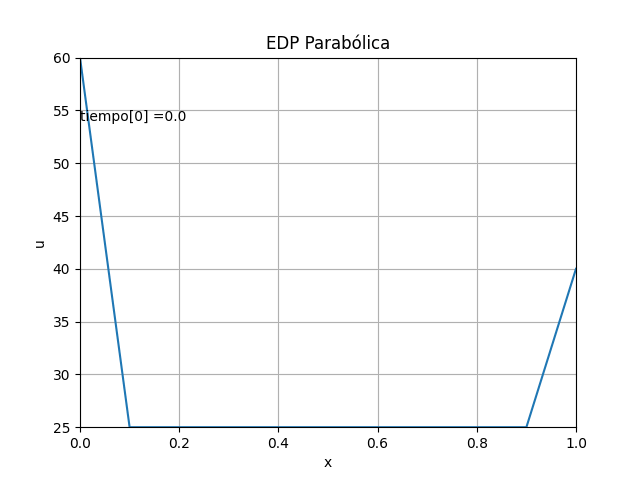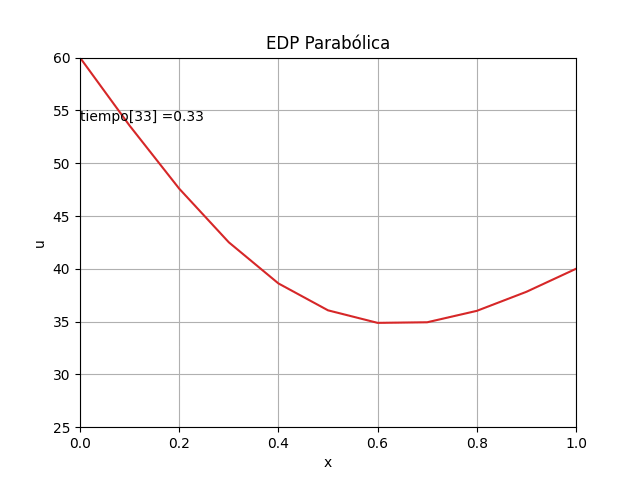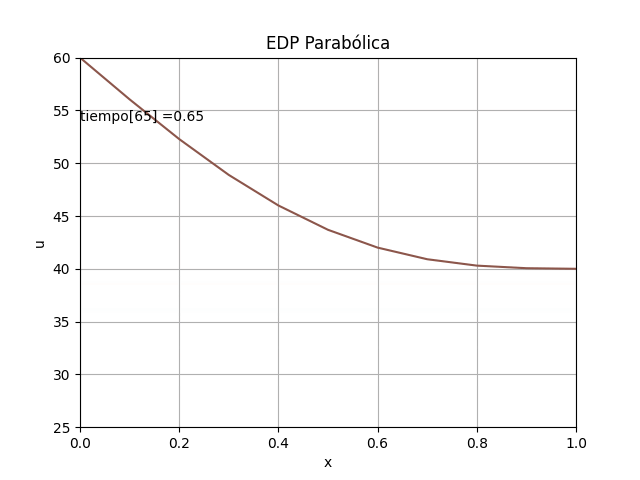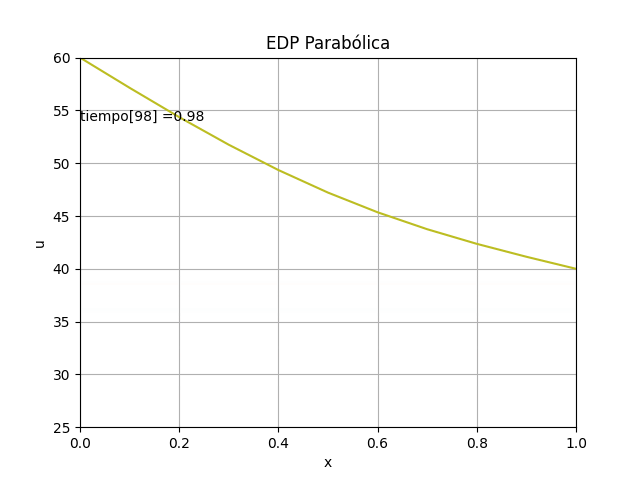
La temperatura se representa en el ejercicio como u[x,t]
\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}o con vista en 3D:
Para la solución numérica, cambia la ecuación a su forma discreta usando diferencias finitas divididas que se sustituyen en la ecuación,
\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} \frac{\partial u}{\partial t} = \frac{u_{i,j+1} - u_{i,j} }{\Delta t}con lo que la ecuación continua se convierte a discreta:
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j+1}-u_{i,j}}{\Delta t}Para interpretar mejor el resultado, se usa una malla que en cada nodo representa la temperatura como los valores u[xi,tj].
Para simplificar nomenclatura se usan los subíndices i para el eje de las x y j para el eje t, quedando u[ i , j ].
En el enunciado del problema habían establecido los valores en las fronteras:
- temperaturas en los extremos Ta, Tb
- la temperatura inicial de la barra T0,
- El parámetro para la barra K.
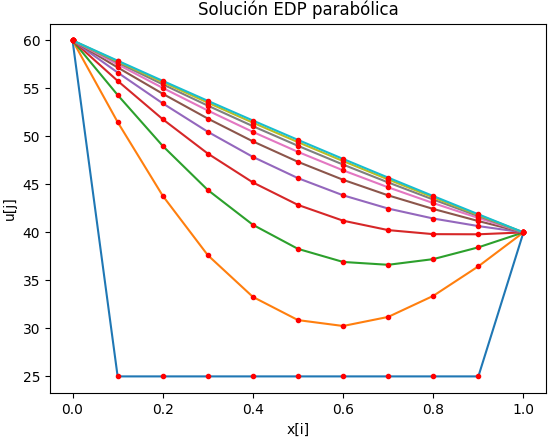
El resultado obtenido se interpreta como los valores de temperatura a lo largo de la barra luego de transcurrido un largo tiempo. Las temperaturas en los extremos de la barra varían entre Ta y Tb a lo largo del tiempo.
Tomando como referencia la malla, existirían algunas formas de plantear la solución, dependiendo de la diferencia finita usada: centrada, hacia adelante, hacia atrás.
EDP Parabólica [ concepto ] Método [ explícito ] [ implícito ]
But what is a partial differential equation? | DE2
3Blue1Brown. 2019 Abril 21
Tarea: Revisar ecuación para difusión de gases, segunda ley de Fick.
La difusión molecular desde un punto de vista microscópico y macroscópico.