EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]
1. Ejercicio
Referencia: Chapra 30.3 p893 pdf917, Burden 9Ed 12.2 p729, Rodríguez 10.2.4 p415
Siguiendo el tema anterior en EDP Parabólicas, se tiene que:
\frac{\partial ^2 u}{\partial x ^2} = K\frac{\partial u}{\partial t}EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]
2. Desarrollo Analítico
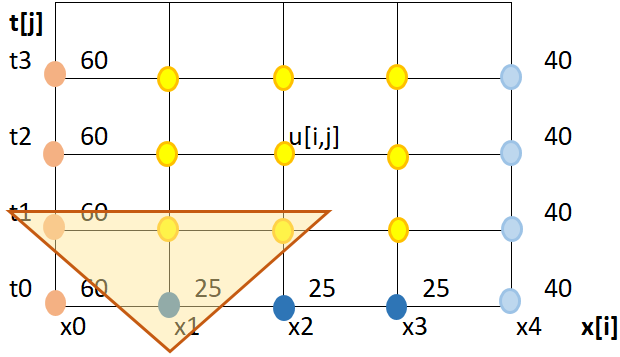
En éste caso se usan diferencias finitas centradas y hacia atrás; la línea de referencia es t1:
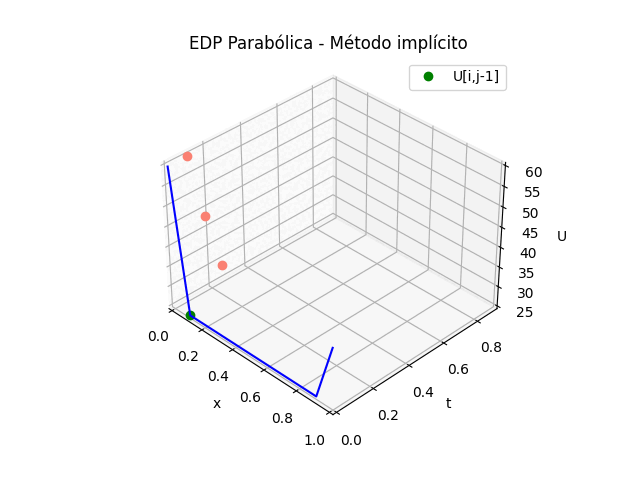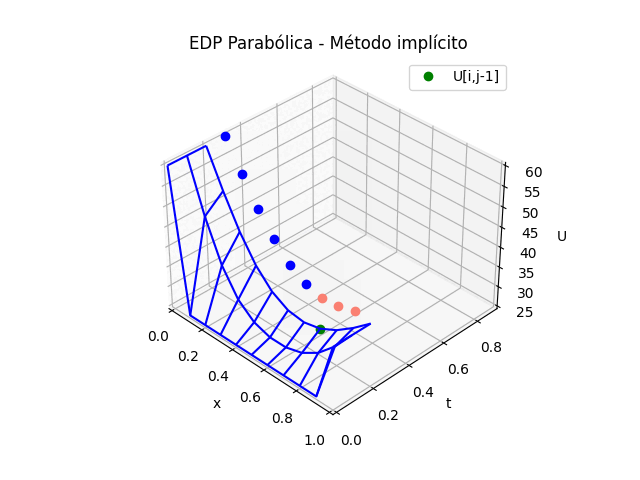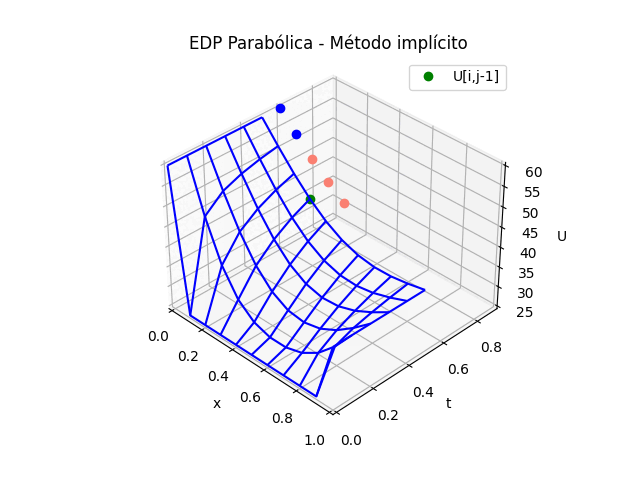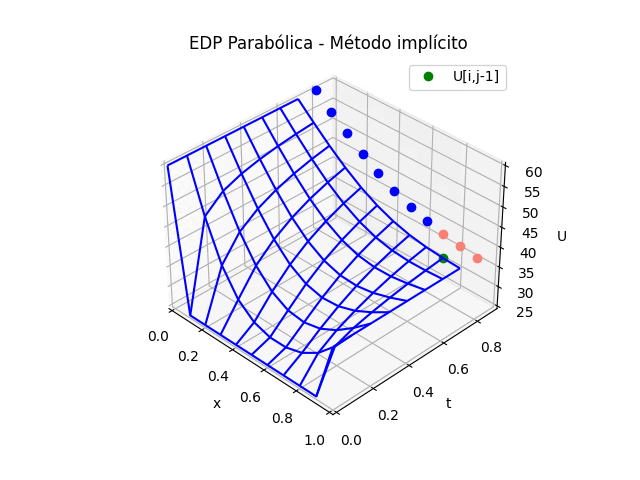
\frac{\partial^2 u}{\partial x^2} = \frac{u_{i+1,j} - 2 u_{i,j} + u_{i-1,j}}{(\Delta x)^2} \frac{\partial u}{\partial t} = \frac{u_{i,j} - u_{i,j-1} }{\Delta t}La selección de las diferencias divididas corresponden a los puntos que se quieren usar para el cálculo, se observan mejor en la gráfica de la malla.
Luego se sustituyen en la ecuación del problema, obteniendo:
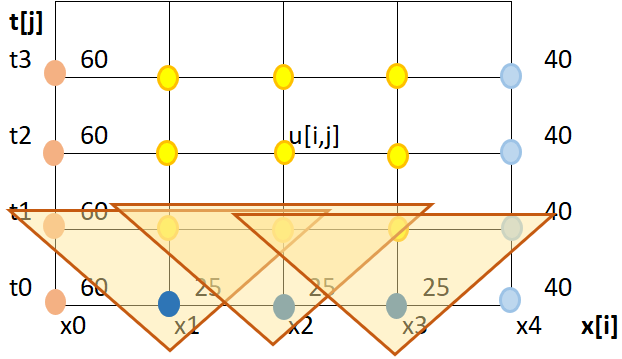
\frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} = K\frac{u_{i,j}-u_{i,j-1}}{\Delta t}De la gráfica se destaca que en la fórmula, dentro del triángulo solo hay DOS valores desconocidos, destacados por los punto en amarillo.
En la ecuación se representa por U[i,j] y U[i+1,j]. Por lo que será necesario crear un sistema de ecuaciones sobre toda la línea de tiempo t1 para resolver el problema.
Despejando la ecuación, se agrupan términos constantes: λ = \frac{\Delta t}{K (\Delta x)^2} .
\lambda u_{i-1,j} + (-1-2\lambda) u_{i,j} + \lambda u_{i+1,j} = -u_{i,j-1}Los parámetro P, Q y R se determinan de forma semejante al método explícito:
P = \lambda Q = -1-2\lambda R = \lambda Pu_{i-1,j} + Qu_{i,j} + Ru_{i+1,j} = -u_{i,j-1}Los valores en los extremos son conocidos, para los puntos intermedios se crea un sistema de ecuaciones para luego usar la forma Ax=B y resolver los valores para cada u(xi,tj).
Por ejemplo con cuatro tramos entre extremos se tiene que:
indice de tiempo es 1 e índice de x es 1.
i=1,j=1
Pu_{0,1} + Qu_{1,1} + Ru_{2,1} = -u_{1,0}i=2,j=1
Pu_{1,1} + Qu_{2,1} + Ru_{3,1} = -u_{2,0}i=3,j=1
Pu_{2,1} + Qu_{3,1} + Ru_{4,1} = -u_{3,0}agrupando ecuaciones y sustituyendo valores conocidos:
\begin{cases} Qu_{1,1} + Ru_{2,1} + 0 &= -T_{0}-PT_{A}\\Pu_{1,1} + Qu_{2,1} + Ru_{3,1} &= -T_{0}\\0+Pu_{2,1}+Qu_{3,1}&=-T_{0}-RT_{B}\end{cases}
que genera la matriz a resolver:
\begin{bmatrix} Q && R && 0 && -T_{0}-PT_{A}\\P && Q && R && -T_{0}\\0 && P && Q && -T_{0}-RT_{B}\end{bmatrix}Use alguno de los métodos de la unidad 3 para resolver el sistema y obtener los valores correspondientes.
Por la extensión de la solución es conveniente usar un algoritmo y convertir los pasos o partes pertinentes a funciones.
Tarea: Revisar y comparar con el método explícito.
EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]
Algoritmos en Python
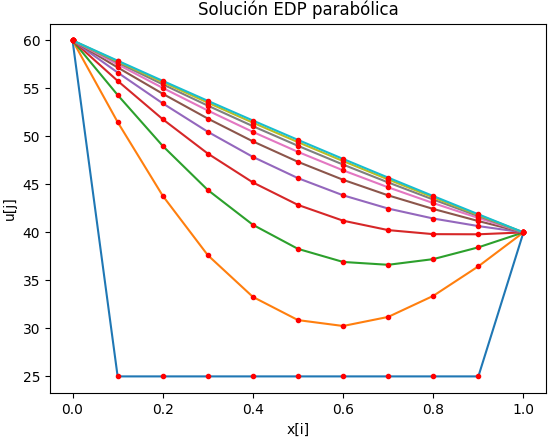
Para la solución con el método implícito, se obtiene el mismo resultado en la gráfica y tabla. Aunque el algoritmo es diferente.
iteración j: 1 A: [[-1.5 0.25 0. 0. 0. 0. 0. 0. 0. ] [ 0.25 -1.5 0.25 0. 0. 0. 0. 0. 0. ] [ 0. 0.25 -1.5 0.25 0. 0. 0. 0. 0. ] [ 0. 0. 0.25 -1.5 0.25 0. 0. 0. 0. ] [ 0. 0. 0. 0.25 -1.5 0.25 0. 0. 0. ] [ 0. 0. 0. 0. 0.25 -1.5 0.25 0. 0. ] [ 0. 0. 0. 0. 0. 0.25 -1.5 0.25 0. ] [ 0. 0. 0. 0. 0. 0. 0.25 -1.5 0.25] [ 0. 0. 0. 0. 0. 0. 0. 0.25 -1.5 ]] B: [-40. -25. -25. -25. -25. -25. -25. -25. -35.] resultado en j: 1 [31.01 26.03 25.18 25.03 25.01 25.01 25.08 25.44 27.57] iteración j: 2 A: [[-1.5 0.25 0. 0. 0. 0. 0. 0. 0. ] [ 0.25 -1.5 0.25 0. 0. 0. 0. 0. 0. ] [ 0. 0.25 -1.5 0.25 0. 0. 0. 0. 0. ] [ 0. 0. 0.25 -1.5 0.25 0. 0. 0. 0. ] [ 0. 0. 0. 0.25 -1.5 0.25 0. 0. 0. ] [ 0. 0. 0. 0. 0.25 -1.5 0.25 0. 0. ] [ 0. 0. 0. 0. 0. 0.25 -1.5 0.25 0. ] [ 0. 0. 0. 0. 0. 0. 0.25 -1.5 0.25] [ 0. 0. 0. 0. 0. 0. 0. 0.25 -1.5 ]] B: [-46.01 -26.03 -25.18 -25.03 -25.01 -25.01 -25.08 -25.44 -37.57] resultado en j: 2 [35.25 27.49 25.55 25.12 25.03 25.05 25.24 26.07 29.39] iteración j: 3 A: [[-1.5 0.25 0. 0. 0. 0. 0. 0. 0. ] [ 0.25 -1.5 0.25 0. 0. 0. 0. 0. 0. ] [ 0. 0.25 -1.5 0.25 0. 0. 0. 0. 0. ] [ 0. 0. 0.25 -1.5 0.25 0. 0. 0. 0. ] [ 0. 0. 0. 0.25 -1.5 0.25 0. 0. 0. ] [ 0. 0. 0. 0. 0.25 -1.5 0.25 0. 0. ] [ 0. 0. 0. 0. 0. 0.25 -1.5 0.25 0. ] [ 0. 0. 0. 0. 0. 0. 0.25 -1.5 0.25] [ 0. 0. 0. 0. 0. 0. 0. 0.25 -1.5 ]] B: [-50.25 -27.49 -25.55 -25.12 -25.03 -25.05 -25.24 -26.07 -39.39] resultado en j: 3 [38.34 29.06 26.09 25.28 25.09 25.13 25.47 26.74 30.72] EDP Parabólica - Método implícito lambda: 0.25 x: [0. 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1. ] t: [0. 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1 ] ... 1.0 Tabla de resultados en malla EDP Parabólica j, U[:,: 10 ], primeras iteraciones 10 [60. 47.43 37.58 31.3 27.98 26.64 26.63 27.83 30.43 34.63 40. ] 9 [60. 46.75 36.68 30.56 27.48 26.3 26.33 27.47 30.04 34.33 40. ] 8 [60. 45.96 35.69 29.8 27.01 26. 26.06 27.12 29.6 33.99 40. ] 7 [60. 45.01 34.6 29.02 26.57 25.73 25.81 26.76 29.13 33.58 40. ] 6 [60. 43.87 33.39 28.24 26.16 25.51 25.58 26.41 28.6 33.09 40. ] 5 [60. 42.45 32.06 27.48 25.8 25.32 25.39 26.07 28.03 32.48 40. ] 4 [60. 40.67 30.61 26.75 25.51 25.18 25.24 25.76 27.41 31.71 40. ] 3 [60. 38.34 29.06 26.09 25.28 25.09 25.13 25.47 26.74 30.72 40. ] 2 [60. 35.25 27.49 25.55 25.12 25.03 25.05 25.24 26.07 29.39 40. ] 1 [60. 31.01 26.03 25.18 25.03 25.01 25.01 25.08 25.44 27.57 40. ] 0 [60. 25. 25. 25. 25. 25. 25. 25. 25. 25. 40.] >>>
Instrucciones en Python
# EDP parabólicas d2u/dx2 = K du/dt # método implícito # Referencia: Chapra 30.3 p.895 pdf.917 # Rodriguez 10.2.5 p.417 import numpy as np # INGRESO # Valores de frontera Ta = 60 Tb = 40 #T0 = 25 # estado inicial de barra fx = lambda x: 25 + 0*x # función inicial para T0 a = 0 # longitud en x b = 1 K = 4 # Constante K dx = 0.1 # Tamaño de paso dt = dx/10 n = 100 # iteraciones en tiempo verdigitos = 2 # decimales a mostrar en tabla de resultados # PROCEDIMIENTO # iteraciones en longitud xi = np.arange(a,b+dx,dx) fi = fx(xi) m = len(xi) ultimox = m-1 ultimot = n-1 # Resultados en tabla u[x,t] u = np.zeros(shape=(m,n), dtype=float) # valores iniciales de u[:,j] j = 0 u[0,:]= Ta u[1:ultimox,j] = fi[1:ultimox] u[ultimox,:] = Tb # factores P,Q,R lamb = dt/(K*dx**2) P = lamb Q = -1 -2*lamb R = lamb # Calcula U para cada tiempo + dt tj = np.arange(0,(n+1)*dt,dt) j = 1 while not(j>=n): # Matriz de ecuaciones k = m-2 A = np.zeros(shape=(k,k), dtype = float) B = np.zeros(k, dtype = float) for f in range(0,k,1): if (f>0): A[f,f-1]=P A[f,f] = Q if (f<(k-1)): A[f,f+1]=R B[f] = -u[f+1,j-1] B[0] = B[0]-P*u[0,j] B[k-1] = B[k-1]-R*u[m-1,j] # Resuelve sistema de ecuaciones C = np.linalg.solve(A, B) # copia resultados a u[i,j] for f in range(0,k,1): u[f+1,j] = C[f] # siguiente iteración j = j + 1 # muestra 3 primeras iteraciones np.set_printoptions(precision=verdigitos) if j<(3+2): print('iteración j:',j-1) print('A:\n',A) print('B:\n',B) print('resultado en j:',j-1,'\n',C) # SALIDA print('EDP Parabólica - Método implícito ') print('lambda: ',np.around(lamb,verdigitos)) print('x:',xi) print('t:',tj[0:len(xi)],'...',tj[-1]) print('Tabla de resultados en malla EDP Parabólica') print('j, U[:,:',ultimox,'], primeras iteraciones') for j in range(ultimox,-1,-1): print(j,u[:,j])
Para realizar la gráfica se aplica lo mismo que en el método explícito
# GRAFICA ------------ import matplotlib.pyplot as plt tramos = 10 salto = int(n/tramos) # evita muchas líneas if (salto == 0): salto = 1 for j in range(0,n,salto): vector = u[:,j] plt.plot(xi,vector) plt.plot(xi,vector, '.',color='red') plt.xlabel('x[i]') plt.ylabel('u[j]') plt.title('Solución EDP parabólica') plt.show()
Sin embargo para la gráfica en 3D se ajustan los puntos de referencia agregados por las diferencias finitas.
# GRAFICA en 3D # vector de tiempo, simplificando en tramos tramos = 10 salto = int(n/tramos) if (salto == 0): salto = 1 tj = np.arange(0,n*dt,dt) tk = np.zeros(tramos,dtype=float) # Extrae parte de la matriz U,acorde a los tramos U = np.zeros(shape=(tramos,m),dtype=float) for k in range(0,tramos,1): U[k,:] = u[:,k*salto] tk[k] = tj[k*salto] # Malla para cada eje X,Y Xi, Yi = np.meshgrid(xi,tk) fig_3D = plt.figure() graf_3D = fig_3D.add_subplot(111, projection='3d') graf_3D.plot_wireframe(Xi,Yi,U, color ='blue',label='EDP Parabólica') graf_3D.plot(Xi[2,0],Yi[2,0],U[2,0],'o',color ='orange') graf_3D.plot(Xi[2,1],Yi[2,1],U[2,1],'o',color ='salmon') graf_3D.plot(Xi[2,2],Yi[2,2],U[2,2],'o',color ='salmon') graf_3D.plot(Xi[1,1],Yi[1,1],U[1,1],'o',color ='green') graf_3D.set_title('EDP Parabólica') graf_3D.set_xlabel('x') graf_3D.set_ylabel('t') graf_3D.set_zlabel('U') graf_3D.legend() graf_3D.view_init(35, -45) plt.show()
Queda por revisar la convergencia y estabilidad de la solución a partir de los O(h) de cada aproximación usada. Revisar los criterios en Chapra 30.2.1 p891, Burden 9Ed 12.2 p727, Rodríguez 10.2.2 p409 .
Tarea o proyecto: Realizar la comparación de tiempos de ejecución entre los métodos explícitos e implícitos. La parte de animación funciona igual en ambos métodos. Los tiempos de ejecución se determinan usando las instrucciones descritas en el enlace: Tiempos de Ejecución en Python
EDP Parabólica [ concepto ] [ ejercicio ]
Método implícito: [ Analítico ] [ Algoritmo ]