Referencia: Rodriguez 6.9.2 p236, Burden 9Ed 3.6 p164
En algunos casos, los datos (x,y) no tienen una relación de tipo funcional y(x), entonces no se pueden aplicar directamente los métodos de interpolación revisados.
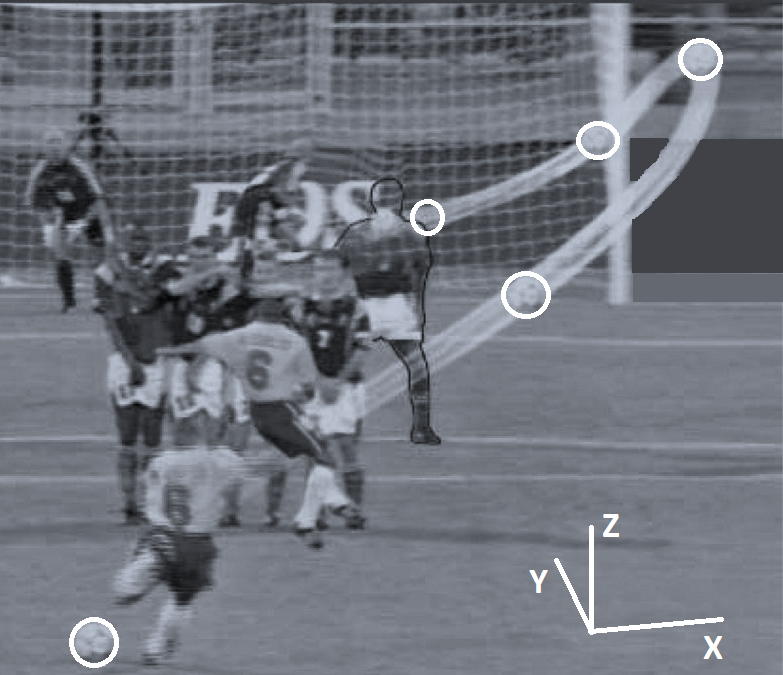
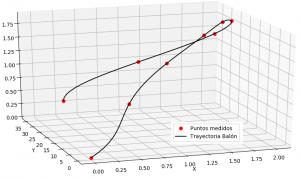
Por ejemplo, en la trayectoria del balón en el «gol imposible», la gráfica de la trayectoria en el espacio o sus proyecciones en los planos dependen del parámetro tiempo «t»en lugar de una relación de x,y,z
Referencia: 1Eva_IT2018_T4 El gol imposible
Tabla de datos:
ti = [0.00, 0.15, 0.30, 0.45, 0.60, 0.75, 0.90, 1.05, 1.20] xi = [0.00, 0.50, 1.00, 1.50, 1.80, 2.00, 1.90, 1.10, 0.30] yi = [0.00, 4.44, 8.88,13.31,17.75,22.19,26.63,31.06,35.50] zi = [0.00, 0.81, 1.40, 1.77, 1.91, 1.84, 1.55, 1.03, 0.30]
Sin embargo si las coordenadas (x,y) se expresan como funciones de otra variable t denominada parámetro, entonces los puntos x(t), y(t) tienen relación funcional, y se pueden construir polinomios de interpolación.
Solución propuesta: s1Eva_IT2018_T4 El gol imposible
Ejemplo
Las coordinadas x(t) y y(t) del recorrido de un cohete registradas en los instantes t fueron:
ti = [0,1,2,3] xti = [2,1,3,4] yti = [0,4,5,0]
Usaremos un algoritmo en Python para mostrar la trayectoria x,y para el problema planteado.
Al realizar la interpolación de los puntos para obtener polinomios que dependen de «t» se obtiene:
px = lambda t: (-2/3)*(t**3) + (7/2)*(t**2) + (-23/6)*t + 2 py = lambda t: (-1/2)*(t**3) + (9/2)*t
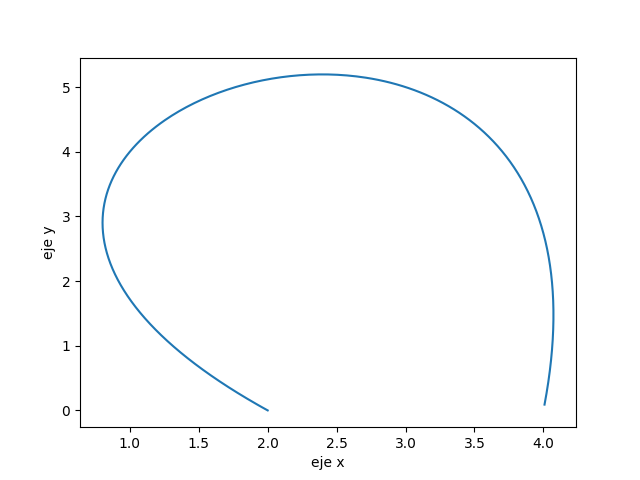
polinomios con los que se puede realizar la gráfica px(t), py(t) en forma separada. Pero para comprender mejor la trayectoria del cohete, se utiliza la gráfica px(t) vs py(t) en el intervalo t entre[0,3]
Las intrucciones para mostrar el resultado son:
# interpolación paramétrica import numpy as np import matplotlib.pyplot as plt # INGRESO ti = [0,1,2,3] xti = [2,1,3,4] yti = [0,4,5,0] # PROCEDIMIENTO # interpolando con lagrange px = lambda t: (-2/3)*(t**3) + (7/2)*(t**2) + (-23/6)*t + 2 py = lambda t: (-1/2)*(t**3) + (9/2)*t t = np.arange(0,3,0.01) puntosx = px(t) puntosy = py(t) # Salida plt.plot(puntosx,puntosy) plt.show()