Referencia: Burden Cap 3. Ejemplo 1.
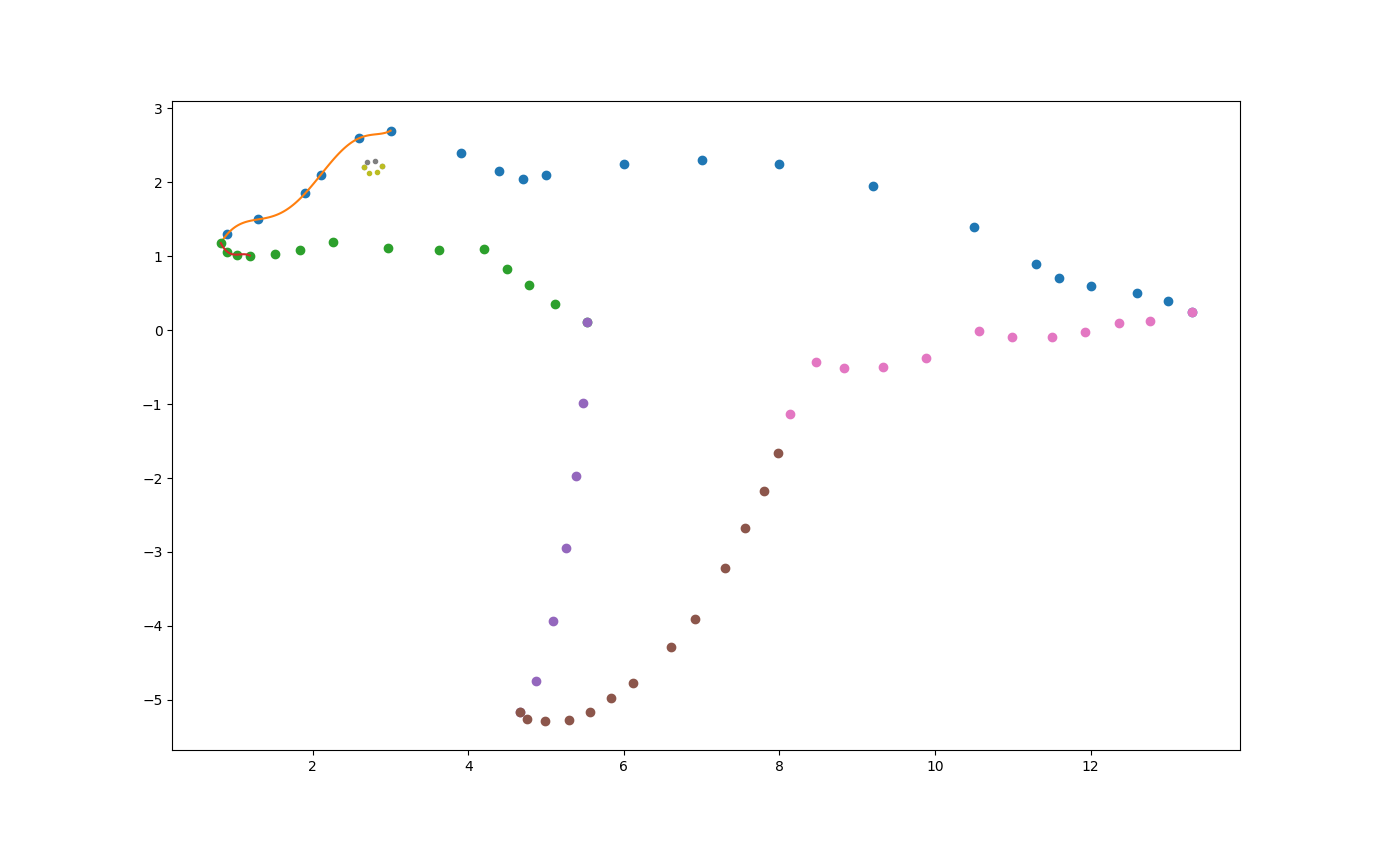
La figura muestra un joven pato en pleno vuelo. Para aproximar el perfil de la parte superior del pato, se presentan 21 puntos a lo largo de la curva de aproximación relativos a un sistema de coordenadas sobrepuestas.
xi = [0.9, 1.3, 1.9, 2.1, 2.6, 3.0, 3.9, 4.4, 4.7, 5, 6.0, 7.0, 8.0, 9.2, 10.5, 11.3, 11.6, 12.0, 12.6, 13.0, 13.3] fi = [1.3, 1.5, 1.85, 2.1, 2.6, 2.7, 2.4, 2.15, 2.05, 2.1, 2.25, 2.3, 2.25, 1.95, 1.4, 0.9, 0.7, 0.6, 0.5, 0.4, 0.25]

a) Realice la interpolación entre puntos usando la interpolación de Lagrange para la parte superior del pato en vuelo.
b) ¿Es posible crear un solo polinomio para los 21 puntos presentados? Explique su respuesta en pocas palabras.
c) ¿En concepto, cuando considera necesario crear un nuevo polinomio?
d) Adjunte en los archivos para: la gráfica que interpola los puntos, y los polinomios que la generan.
e) (Puntos extra: 10, para promediar con lección o taller)
Se adjuntan los demás puntos del perfil del pato en pleno vuelo, presente el o los polinomios que interpolan la figura (gráfica y polinomios), las despuestas a literales b,c,d deben también ser válidas para el ejercicio completo.
# Perfil Superior del pato xiA = [0.9, 1.3, 1.9, 2.1, 2.6, 3.0, 3.9, 4.4, 4.7, 5, 6.0, 7.0, 8.0, 9.2, 10.5, 11.3, 11.6, 12.0, 12.6, 13.0, 13.3] fiA = [1.3, 1.5, 1.85, 2.1, 2.6, 2.7, 2.4, 2.15, 2.05, 2.1, 2.25, 2.3, 2.25, 1.95, 1.4, 0.9, 0.7, 0.6, 0.5, 0.4, 0.25] # Perfil inferior cabeza xiB = [0.817, 0.897, 1.022, 1.191, 1.510, 1.834, 2.264, 2.962, 3.624, 4.202, 4.499, 4.779, 5.109, 5.527] fiB = [1.180, 1.065, 1.023, 1.010, 1.032, 1.085, 1.192, 1.115, 1.087, 1.100, 0.830, 0.608, 0.350, 0.106] # Perfil Ala superior xiC = [4.659, 4.865, 5.085, 5.261, 5.387, 5.478, 5.527] fiC = [-5.161, -4.741, -3.933, -2.951, -1.970, -0.981, 0.106] # Perfil Ala inferior xiD = [4.659, 4.750, 4.990, 5.289, 5.560, 5.839, 6.113, 6.606, 6.916, 7.305, 7.563, 7.802, 7.983] fiD = [-5.161, -5.259, -5.284, -5.268, -5.161, -4.982, -4.769, -4.286, -3.911, -3.213, -2.670, -2.176, -1.655] # Perfil inferior posterior xiE = [8.141, 8.473, 8.832, 9.337, 9.887, 10.572, 10.995, 11.501, 11.923, 12.364, 12.763, 13.300] fiE = [-1.138, -0.434, -0.514, -0.494, -0.382, -0.005, -0.090, -0.085, -0.030, 0.093, 0.120, 0.250] # Perfil ojo superior xiF = [2.663, 2.700, 2.805, 2.886] fiF = [2.202, 2.279, 2.293, 2.222] # Perfil ojo inferior xiG = [2.663, 2.720, 2.826, 2.886] fiG = [2.202, 2.130, 2.143, 2.222]