[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
Referencia: Chapra 9.4.2 p268. Burden 6.2 p279. Rodríguez 4.0 p105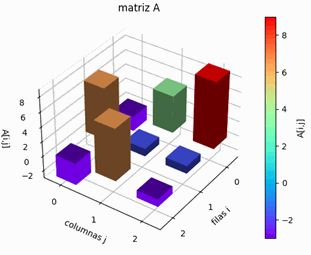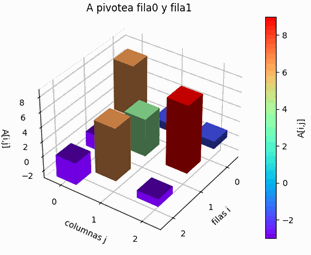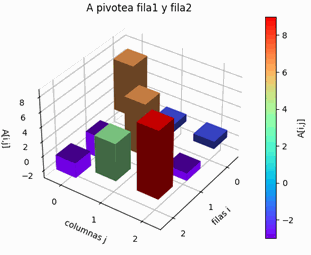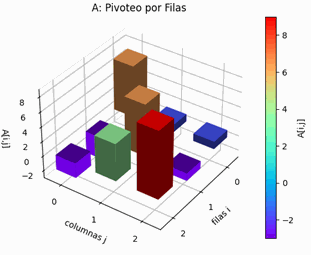
Los métodos de solución a sistemas de ecuaciones en los primeros pasos usan la matriz aumentada y pivoteada por filas.
Como es un procedimiento usado en todos los métodos de la unidad, para simplificar se presenta como uno de los primeros algoritmos.
El objetivo del pivoteo es ordenar la matriz para que en lo posible sea diagonal dominante.
|a_{i,i}| \geq \sum_{j=0 ; i\neq j}^n |a_{i,j}|1. Ejercicio
Referencia: 1Eva_IIT2011_T2 Sistema de Ecuaciones, diagonal dominante
Considere el siguiente sistema de ecuaciones AX=B dado por:
\begin{cases} -2x+5y+9z=1\\7x+y+z=6\\-3x+7y-z=-26\end{cases}Realice el pivoteo parcial por filas, de tal manera que la diagonal de A sea estrictamente dominante.
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
..
2. Matriz Aumentada
El sistema de ecuaciones se escribe en la forma algebraica como matrices y vectores de la forma Ax=B
\begin{pmatrix} -2 & 5 & 9 \\ 7 & 1 & 1 \\-3 & 7 & -1 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 1 \\ 6 \\ -26 \end{pmatrix}Para el algoritmo, las ecuaciones se escriben en forma de matriz A y vector B.
A = [[-2, 5, 9],
[ 7, 1, 1],
[-3, 7,-1]]
B = [1,6,-26]
Las matrices y vectores se procesan como arreglos np.array() de números reales. No se usan listas.
A = np.array(A,dtype=float) B = np.array(B,dtype=float)
El vector B para la matriz aumentada se usa en forma de columna. Se aumenta una dimensión [B] y se aplica la transpuesta.
B_columna = np.transpose([B])
>>> B_columna
array([[ 1],
[ 6],
[-26]])
La matriz aumentada AB se forma al concatenar por columnas la matriz A con el vector B_columna, usando el parámetro axis=1.
AB = np.concatenate((A,B_columna),axis=1)
el resultado AB se muestra como:
>>> AB
array([[ -2. , 5. , 9. , 1.],
[ 7. , 1. , 1. , 6.],
[ -3. , 7. , -1. , -26.]])
\left( \begin{array}{rrr|r} -2 & 5 & 9 & 1 \\ 7 & 1 & 1 & 6 \\ -3 & 7 & -1 & -26 \end{array} \right)
En varios algoritmos se usa la matriz aumentada AB, para mantener el orden entre filas de A y B al aplicar cambios de fila.
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
..
3. Pivoteo parcial por filas
Para el pivoteo por filas de la matriz aumentada AB, tiene como primer paso revisar la primera columna, desde la posición diagonal hacia todas las filas por debajo, usando solo la magnitud de los coeficientes |A|.
La representación gráfica de la matriz A, permite visualizar los intercambios de fila.
>>> AB array([[ -2. , 5. , 9. , 1.], [ 7. , 1. , 1. , 6.], [ -3. , 7. , -1. , -26.]])
Las instrucciones para seleccionar la columna, usar el valor absoluto y dónde se encuentra el máximo son:
columna = abs(AB[i:,i])
dondemax = np.argmax(columna)
Los valores de la columna se reducen a:
columna = [|-2.|, fila=0
| 7.|, fila=1
|-3.|] fila=2
dondemax = 1
Si la magnitud de mayor valor no está en la diagonal (dondemax≠0), se realiza el intercambio entre la fila dondemax y la fila de la diagonal i en AB.
AB = [[ 7. , 1. , 1. , 6.],
[ -2. , 5. , 9. , 1.],
[ -3. , 7. , -1. , -26.]]
En éste paso se asegura que en la casilla AB[0,0] se encuentre el mayor valor de la columna 1.
El intercambio de filas requiere tres pasos: realizar una copia de la fila que se esta analizando en un vector temporal. Luego se copian los valores en la fila AB[dondemax+i] en la fila AB[i]. Finalmente actualizando la fila AB[dondemax+i] con los valores de temporal.
if (dondemax !=0): # NO en diagonal # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal
Se repite el proceso anterior para la siguiente columna (j=1), pero siempre formada desde la diagonal (i=j).
La columna en éste paso se reduce el tamaño en una posición. Se consideran solo las magnitudes para la selección de dondemax.
AB = [[ 7. , 1. , 1. , 6.],
[ -2. , 5. , 9. , 1.],
[ -3. , 7. , -1. , -26.]]
Los valores de la columna se reducen a:
columna = [|5|, fila=0
|7|] fila=1
dondemax = 1
En el ejercicio se encuentra que: la magnitud de mayor valor está en la fila=1, no en la diagonal. Se realiza el intercambio entre la fila ‘i’ y la fila (dondemax+i) de AB.
AB = ([[ 7. , 1. , 1. , 6.],
[ -3. , 7. , -1. , -26.],
[ -2. , 5. , 9. , 1.]]
Se repite el proceso para la tercera columna desde la diagonal, que resulta tener solo una casilla (columna =[9]) y no ser requiere continuar.
En la gráfica se destaca el resultado del pivoteo por filas, acercando en lo posible a una matriz diagonal dominante.
Pivoteo parcial por filas AB: [[ 7. , 1. , 1. , 6.], [ -3. , 7. , -1. , -26.], [ -2. , 5. , 9. , 1.]] A: [[ 7. , 1. , 1.], [ -3. , 7. , -1.], [ -2. , 5. , 9.]] B: [6. , -26. , 1.]
Tarea: Revisar cuando en una columna se tiene dos valores mayores de igual valor. Ampliar el algoritmo. Considere como ejemplo del caso planteado: 1Eva_IT2011_T2_MN Alimentos para animales
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
..
4. Algoritmo en Python
Para realizar el algoritmo, es de recordar que para realizar operaciones en una matriz sin alterar la original, se usa una copia de la matriz (np.copy). Con la copia de la matriz, se puede comparar y observar los cambios entre la matriz original y la copia a la que se aplicaron cambios.
Si no es necesaria la comparación entre el antes y después, no se realiza la copia y se ahorra el espacio de memoria, detalle importante para matrices de «gran tamaño» y una computadora con «limitada» memoria.
# Pivoteo parcial por filas import numpy as np # INGRESO A = [[-2, 5, 9], [ 7, 1, 1], [-3, 7,-1]] B = [1,6,-26] # PROCEDIMIENTO # Matrices como arreglo, numeros reales A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada AB B_columna = np.transpose([B]) AB = np.concatenate((A,B_columna),axis=1) AB0 = np.copy(AB) # copia de AB # Pivoteo parcial por filas tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = abs(AB[i:,i]) dondemax = np.argmax(columna) if (dondemax !=0): # NO en diagonal # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal # Actualiza A y B pivoteado A = AB[:,:n] B = AB[:,n] # SALIDA print('Matriz aumentada:') print(AB0) print('Pivoteo parcial por filas AB:') print(AB) print('A:') print(A) print('B:') print(B)
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
..
5. Función pivoteafila(M)
Los bloques de cada procedimiento que se repiten en otros métodos se convierten a funciones def-return, empaquetando las soluciones algorítmicas.
# Pivoteo parcial por filas, funcion import numpy as np def pivoteafila(A,B,vertabla=False): ''' Pivoteo parcial por filas, entrega matriz aumentada AB Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) if vertabla==True: print('Matriz aumentada') print(AB) print('Pivoteo parcial:') # Pivoteo por filas AB tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(' ',pivoteado, 'intercambiar filas: ',i, 'con', dondemax+i) if vertabla==True: if pivoteado==0: print(' Pivoteo por filas NO requerido') else: print(AB) return(AB) # INGRESO A = [[-2, 5, 9], [ 7, 1, 1], [-3, 7,-1]] B = [1,6,-26] # PROCEDIMIENTO AB = pivoteafila(A,B,vertabla=True) n = len(AB) # Actualiza A y B pivoteado A = AB[:,:n] B = AB[:,n] # SALIDA print('Pivoteo parcial por filas AB:') print(AB) print('A:') print(A) print('B:') print(B)
El resultado del ejercicio es:
Matriz aumentada [[ -2. 5. 9. 1.] [ 7. 1. 1. 6.] [ -3. 7. -1. -26.]] Pivoteo parcial: 1 intercambiar filas: 0 con 1 2 intercambiar filas: 1 con 2 [[ 7. 1. 1. 6.] [ -3. 7. -1. -26.] [ -2. 5. 9. 1.]] Pivoteo parcial por filas AB: [[ 7. 1. 1. 6.] [ -3. 7. -1. -26.] [ -2. 5. 9. 1.]] A: [[ 7. 1. 1.] [-3. 7. -1.] [-2. 5. 9.]] B: [ 6. -26. 1.]
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
6. Gráfica de Matriz A en 3D
Instrucciones para la gráfica en 3D de una matriz A. Las alturas de las barras son relativas a los valores de la casilla A[i,j]
# Matriz A como Barras3D import numpy as np import matplotlib.pyplot as plt # INGRESO ##A = [[-2, 5, 9], ## [ 7, 1, 1], ## [-3, 7,-1]] ##titulo = 'matriz A' ##A = [[ 7, 1, 1], ## [-2, 5, 9], ## [-3, 7,-1]] ##titulo = 'A pivotea fila0 y fila1' ##A = [[ 7, 1, 1], ## [-3, 7,-1], ## [-2, 5, 9]] ##titulo = 'A pivotea fila1 y fila2' A = [[ 7, 1, 1], [-3, 7,-1], [-2, 5, 9]] titulo='A: Pivoteo por Filas' # PROCEDIMIENTO A = np.array(A, dtype=float) n,m = np.shape(A) # para grafica 3D xi = np.arange(0,n,1) yj = np.arange(0,m,1) Xi,Yj = np.meshgrid(xi,yj) A_min = np.min([np.min(A),-3]) A_max = np.max([np.max(A),9]) # SALIDA # Grafica barras 3D fig3D = plt.figure() graf3D = fig3D.add_subplot(111,projection='3d') AT = np.transpose(A) # filas en x, columnas en y h = 0.5 # Barras ancho y profundidad color_A = AT.ravel()/A_max color_ij = plt.cm.rainbow(color_A) graf3D.bar3d(Xi.ravel(),Yj.ravel(), np.zeros(n*m),h,h, AT.ravel(),color=color_ij) # escala eje z graf3D.set_zlim(A_min,A_max) # etiqueta graf3D.set_xlabel('filas i') graf3D.set_ylabel('columnas j') graf3D.set_zlabel('A[i,j]') graf3D.set_title(titulo) # etiquetas ejes graf3D.xaxis.set_ticks(xi + h/2) graf3D.xaxis.set_ticklabels(xi) graf3D.yaxis.set_ticks(yj + h/2) graf3D.yaxis.set_ticklabels(yj) # Barra de color color_escala = plt.Normalize(A_min,A_max) color_barra = plt.cm.ScalarMappable(norm=color_escala, cmap=plt.colormaps["rainbow"]) fig3D.colorbar(color_barra,ax=graf3D,label="A[i,j]") graf3D.view_init(35,35) plt.show()
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]
7. Ejercicio 2
Referencia: Rodríguez 4.0 p105, 1Eva_IT2010_T3_MN Precio artículos
Ejemplo 1. Un comerciante compra tres productos A, B, C, pero en las facturas únicamente consta la cantidad comprada en Kg y el valor total de la compra.
Se necesita determinar el precio unitario de cada producto. Dispone de solo tres facturas con los siguientes datos:
| Cantidad | Valor ($) | |||
| Factura | X0 | X1 | X2 | Pagado |
|---|---|---|---|---|
| 1 | 4 | 2 | 5 | 60.70 |
| 2 | 2 | 5 | 8 | 92.90 |
| 3 | 5 | 4 | 3 | 56.30 |
Los precios unitarios se pueden representar por las variables x0, x1, x2 para escribir el sistema de ecuaciones que muestran las relaciones de cantidad, precio y valor pagado:
\begin{cases} 4x_0+2x_1+5x_2 = 60.70 \\ 2x_0+5x_1+8x_2 = 92.90 \\ 5x_0+4x_1+3x_2 = 56.30 \end{cases}Desarrollo
El sistema de ecuaciones se escribe en la forma algebraica como matrices y vectores de la forma Ax=B
\begin{pmatrix} 4 & 2 & 5 \\ 2 & 5 & 8 \\5 & 4 & 3 \end{pmatrix} \begin{pmatrix} x_0 \\ x_1 \\ x_2 \end{pmatrix} = \begin{pmatrix} 60.70 \\ 92.90 \\ 56.30 \end{pmatrix}La matriz aumentada usando el algoritmo tiene como resultado:
>>> AB
array([[ 4. , 2. , 5. , 60.7],
[ 2. , 5. , 8. , 92.9],
[ 5. , 4. , 3. , 56.3]])
En varios algoritmos se usa la matriz aumentada AB, para mantener el orden entre filas al aplicar cambios de fila.
Para el pivoteo por fila de la matriz aumentada AB, tiene como primer paso revisar la primera columna desde la diagonal en adelante.
>>> AB
array([[ 4. , 2. , 5. , 60.7],
[ 2. , 5. , 8. , 92.9],
[ 5. , 4. , 3. , 56.3]])
Los valores de la columna se reducen a:
columna = [|4|, fila=0
|2|, fila=1
|5|] fila=2
dondemax = 2
En el ejercicio se encuentra que: la magnitud de mayor valor está en la última fila, no en la diagonal. Se realiza el intercambio entre la fila 2 y la fila 0 de AB.
AB = [[ 5. , 4. , 3. , 56.3],
[ 2. , 5. , 8. , 92.9],
[ 4. , 2. , 5. , 60.7]]
Se repite el proceso anterior para la siguiente columna, pero siempre formada desde la diagonal.
AB = [[ 5. , 4. , 3. , 56.3],
[ 2. , 5. , 8. , 92.9],
[ 4. , 2. , 5. , 60.7]]
Los valores de la columna se reducen a:
columna = [|5|, fila=0
|2|] fila=1
dondemax = 0
Como la posición dondemax es la primera, índice 0, se determina que ya está en la diagonal de AB y no es necesario realizar el intercambio de filas.
Se repite el proceso para la tercera columna desde la diagonal, que resulta tener solo una casilla (columna =[5]) y no ser requiere continuar.
El resultado del pivoteo por fila se muestra a continuación:
Pivoteo parcial por filas AB: [[ 5. 4. 3. 56.3] [ 2. 5. 8. 92.9] [ 4. 2. 5. 60.7]] A: [[5. 4. 3.] [2. 5. 8.] [4. 2. 5.]] B: [56.3 92.9 60.7]
[ Ejercicio ] [ Matriz Aumentada ] [ Pivoteo filas ] [ algoritmo ] [ función ]