s1Eva_2021PAOI_T1 Función recursiva y raíces de ecuaciones

Ejercicio: 1Eva_2021PAOI_T1 Función recursiva y raíces de ecuaciones

Literal a

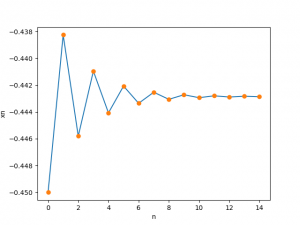
Evaluando las sucesión de la forma recursiva:

xi
[-0.45       -0.4383     -0.4458     -0.441      -0.4441 
 -0.4421     -0.4434     -0.4425     -0.4431     -0.4427
 -0.4429     -0.4428     -0.4429     -0.4428     -0.4429]
errores
[ 1.1745e-02 -7.5489e-03  4.8454e-03 -3.1127e-03  1.9986e-03
 -1.2837e-03  8.2430e-04 -5.2939e-04  3.3996e-04 -2.1833e-04
  1.4021e-04 -9.0044e-05  5.7826e-05 -3.7136e-05  0.0000e+00]

literal b

Se puede afirmar que converge, observe la diferencia entre cada dos valores consecutivos de la sucesión … (continuar de ser necesario)

literal c

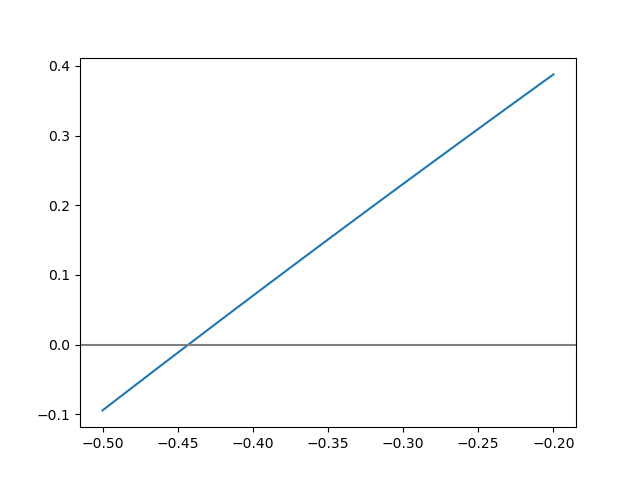
Para el algoritmo se requiere la función f(x) y su derivada f'(x)

f(x) = x +ln(x+2)

f'(x) = 1 + \frac{1}{x+2}

x₀ = -0.45

itera = 1

x_{i+1} = x_i -\frac{f(x_i)}{f'(x_i)}

x_{1} = x_0 -\frac{f(x_0)}{f'(x_0)} = -0.45 -\frac{-0.45+ln(-0.45+2)}{1 + \frac{1}{-0.45+2}}

x₁ = -0.44286

error = |x₁-x₀| = |-0.44286 -(-0.45)| = 0.007139

itera = 2

x_{2} = -0.4428 -\frac{-0.4428 + ln(-0.45+2)}{1 + \frac{1}{-0.4428+2}}

x₁ = -0.44286

error = |x₁-x₀| = |-0.44285 -(-4.4286)| = 6.4394e-06

con lo que se cumple el valor de tolerancia y no se requiere otra iteración

la raiz se encuentra en x = -0.44286

Solución con algoritmo

xi
[-0.45       -0.4383     -0.4458     -0.441      -0.4441 
 -0.4421     -0.4434     -0.4425     -0.4431     -0.4427
 -0.4429     -0.4428     -0.4429     -0.4428     -0.4429]
errores
[ 1.1745e-02 -7.5489e-03  4.8454e-03 -3.1127e-03  1.9986e-03
 -1.2837e-03  8.2430e-04 -5.2939e-04  3.3996e-04 -2.1833e-04
  1.4021e-04 -9.0044e-05  5.7826e-05 -3.7136e-05  0.0000e+00]
['xi', 'xnuevo', 'tramo']
[[-4.5000e-01 -4.4286e-01  7.1392e-03]
 [-4.4286e-01 -4.4285e-01  6.4394e-06]]
raiz en:  -0.44285440100759543
con error de:  6.439362322474551e-06
>>>

Instrucciones en Python

import numpy as np
import matplotlib.pyplot as plt

# literal a sucesión en forma recursiva
def secuenciaL(n,x0):
    if n == 0:
        xn = x0
    if n>0:
        xn = np.log(1/(2+secuenciaL(n-1,x0)))
    return(xn)
x0 = -0.45
n = 15
xi = np.zeros(n,dtype=float)
xi[0] = x0
errado = np.zeros(n,dtype=float)
for i in range(1,n,1):
    xi[i] = secuenciaL(i,x0)
    errado[i-1] = xi[i] - xi[i-1]
   
np.set_printoptions(precision=4)
print('xi: ')
print(xi)
print('errado: ')
print(errado)

#Grafica literal a y b
plt.plot(xi)
plt.plot(xi,'o')
plt.xlabel('n')
plt.ylabel('xn')
plt.show()

# Método de Newton-Raphson
# Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61)

import numpy as np

# INGRESO
fx  = lambda x: x+np.log(x+2)
dfx = lambda x: 1+ 1/(x+2)

x0 = -0.45
tolera = 0.0001

a = -0.5
b = -0.2
muestras = 21
# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# para la gráfica
xj = np.linspace(a,b,muestras)
fj = fx(xj)

# SALIDA
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)

plt.plot(xj,fj)
plt.axhline(0, color='grey')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()