Ejercicio: 1Eva_2022PAOI_T3 Interpolar crecimiento de contagios
| Día del mes | 1 | 8 | 15 | 22 |
| Contagios | 1 | 5.6 | 27 | 43.5 |
a) Realice el planteamiento del sistema de ecuaciones que se usaría usando el método de interpolación polinómica.
El modelo de polinomio de grado máximo que se puede obtener es grado 3:
p_3(t) = a_0 + a_1 t + a_2 t^2 + a_3 t^3por lo que usando los valores de los puntos dados en la tabla:
p_3(1) = a_0 + a_1 (1) + a_2 (1)^2 + a_3 (1)^3 = 1 p_3(8) = a_0 + a_1 (8) + a_2 (8)^2 + a_3 (8)^3 = 5.6 p_3(15) = a_0 + a_1 (15) + a_2 (15)^2 + a_3 (15)^3 = 27 p_3(22) = a_0 + a_1 (22) + a_2 (22)^2 + a_3 (22)^3 = 43.5b) Realice el planteamiento del sistema de ecuaciones en su forma matricial y muestre la matriz aumentada.
\begin{pmatrix} 1 & 1 & 1^2 & 1^2\\ 1 & 8 & 8^2 & 8^3 \\ 1 & 15 & 15^2 & 15^3 \\ 1 & 22 & 22^2 & 22^3 \end{pmatrix} \begin{pmatrix} a_0 \\ a_1 \\ a_2 \\ a_3 \end{pmatrix} \begin{pmatrix} 1 \\ 56 \\ 27 \\43.5 \end{pmatrix}matriz aumentada,
\begin{pmatrix} 1 & 1 & 1^2 & 1^2 & 1 \\ 1 & 8 & 8^2 & 8^3 & 56 \\ 1 & 15 & 15^2 & 15^3 & 27\\ 1 & 22 & 22^2 & 22^3 & 43.5\end{pmatrix}c) Desarrolle el pivoteo parcial por filas, indicando las operaciones realizadas en éste proceso
pivoteo parcial por filas
\begin{pmatrix} 1 & 1 & 1^2 & 1^2 & 1 \\ 1 & 22 & 22^2 & 22^3 & 43.5 \\ 1 & 15 & 15^2 & 15^3 & 27 \\ 1 & 8 & 8^2 & 8^3 & 56\end{pmatrix}d) Usando el método directo de Gauss-Jordan, muestre las expresiones necesarias para el algoritmo.
eliminación hacia adelante
\begin{pmatrix} 1 & 1 & 1^2 & 1^2 & 1 \\ 1-1 & 22-1 & 22^2-1^2 & 22^3 -1^3& 43.5 - 1\\ 1-1 & 15-1 & 15^2 -1^2& 15^3 -1^3& 27 -1\\ 1-1 & 8-1 & 8^2 -1^2& 8^3 -1^3& 56-1\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 14 & 224 & 3376& 26\\ 0 & 7 & 63& 511 & 55\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 14-\frac{14}{21} 21 & 224-\frac{14}{21}483& 3376 -\frac{14}{21}10647& 26-\frac{14}{21}42.5\\ 0 & 7-\frac{7}{21}21 & 63-\frac{7}{21}483& 511-\frac{7}{21}10647 & 55-\frac{7}{21}42.5\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 0 &-98 & -3722& -2.33 \\ 0 & 0 & -98 & -3038 & 40.83 \end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 0 &-98 & -3722& -2.33 \\ 0 & 0 & -98-\frac{98}{-98}98 & -3038 -\frac{98}{-98}3722& 40.83 -\frac{98}{-98}(-2.33)\end{pmatrix} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 \\ 0 & 21 & 483 & 10647& 42.5 \\ 0 & 0 &-98 & -3722& -2.33 \\ 0 & 0 & 0 & 686 & -7.23\end{pmatrix}realizando el proceso de eliminación hacia atrás, semejante al método anterior se obtiene
\begin{pmatrix} 1 & 0 & 0 & 0 & 2.98\\ 0 & 1 & 0 & 0& -2.39 \\ 0 & 0 & 1 & 0 & 0.424 \\ 0 & 0 & 0 &1 & -0.0105\end{pmatrix}con lo que el vector resultado es:
X= [2.98, -2.39, 0.42, -0.0105]El polinomio de interpolación resultante es:
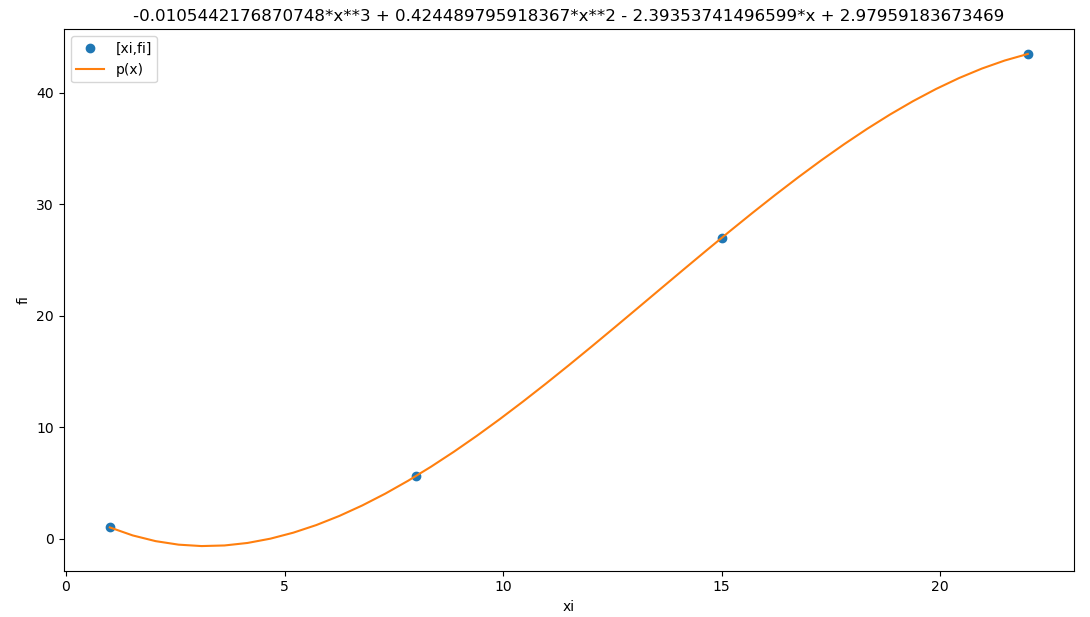
p(t)= 2.98 -2.39 t + 0.42 t^2 -0.0105 t^3e) Para el día 19 se encuentra que el valor correspondiente a contagios es de 37%. Estime el error presentado del modelo para ese día.
p(19)= 2.98 -2.39 (19) + 0.42 (19)^2 -0.0105 (19)^3 = 38.42 error = |38.42-37| = 1.42f) Desarrolle el ejercicio usando otro método para encontrar el polinomio de interpolación.
usando diferencias finitas
Tabla Diferencia Finita [['i', 'xi', 'fi', 'df1', 'df2', 'df3', 'df4']] [[ 0. 1. 1. 4.6 16.8 -21.7 0. ] [ 1. 8. 5.6 21.4 -4.9 0. 0. ] [ 2. 15. 27. 16.5 0. 0. 0. ] [ 3. 22. 43.5 0. 0. 0. 0. ]]
polinomio:
p(t) = 1+\frac{4.6}{1! (7)}(t-1) + + \frac{16.8}{2!(7^2)}(t-1)(t-8) + +\frac{-21.7}{3!(7^3}(t-1)(t-8)(t-15)Algoritmo en Python
Para literal f
# Polinomio interpolación # Diferencias finitas avanzadas # Tarea: Verificar tamaño de vectores, # verificar puntos equidistantes en x import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO , Datos de prueba xi = np.array([1,8,15,22],dtype=float) fi = np.array([1,5.6,27,43.5],dtype=float) # PROCEDIMIENTO # Tabla de Diferencias Finitas titulo = ['i','xi','fi'] n = len(xi) ki = np.arange(0,n,1) tabla = np.concatenate(([ki],[xi],[fi]),axis=0) tabla = np.transpose(tabla) # diferencias finitas vacia dfinita = np.zeros(shape=(n,n),dtype=float) tabla = np.concatenate((tabla,dfinita), axis=1) # Calcula tabla, inicia en columna 3 [n,m] = np.shape(tabla) diagonal = n-1 j = 3 while (j < m): # Añade título para cada columna titulo.append('df'+str(j-2)) # cada fila de columna i = 0 while (i < diagonal): tabla[i,j] = tabla[i+1,j-1]-tabla[i,j-1] i = i+1 diagonal = diagonal - 1 j = j+1 # POLINOMIO con diferencias Finitas avanzadas # caso: puntos equidistantes en eje x h = xi[1] - xi[0] dfinita = tabla[0,3:] n = len(dfinita) # expresión del polinomio con Sympy x = sym.Symbol('x') polinomio = fi[0] for j in range(1,n,1): denominador = np.math.factorial(j)*(h**j) factor = dfinita[j-1]/denominador termino = 1 for k in range(0,j,1): termino = termino*(x-xi[k]) polinomio = polinomio + termino*factor # simplifica multiplicando entre (x-xi) polisimple = polinomio.expand() # polinomio para evaluacion numérica px = sym.lambdify(x,polisimple) # Puntos para la gráfica muestras = 101 a = np.min(xi) b = np.max(xi) pxi = np.linspace(a,b,muestras) pfi = px(pxi) # SALIDA print('Tabla Diferencia Finita') print([titulo]) print(tabla) print('dfinita: ') print(dfinita) print('polinomio: ') print(polinomio) print('polinomio simplificado: ' ) print(polisimple) # Gráfica plt.plot(xi,fi,'o', label = 'Puntos') ##for i in range(0,n,1): ## plt.axvline(xi[i],ls='--', color='yellow') plt.plot(pxi,pfi, label = 'Polinomio') plt.legend() plt.xlabel('xi') plt.ylabel('fi') plt.title('Interpolación polinómica') plt.show()