s1Eva_2022PAOII_T1 Esfera flotando en agua

Ejercicio: 1Eva_2022PAOII_T1 Esfera flotando en agua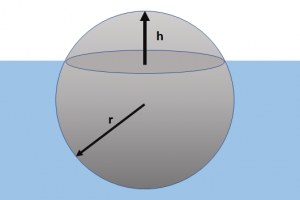

Según el principio de Arquímedes, la fuerza de flotación o empuje es igual al peso de el fluido desplazado por la porción sumergida de un objeto.

F_{empuje} = F_{peso} \rho_{agua} V_{sumergido} \text{ } g = \rho_{esfera}V_{esfera} \text{ } g V_{sumergido} = \frac{\rho_{esfera}}{\rho_{agua}}V_{esfera} V_{esfera} - V_{sobreagua} = \frac{\rho_{esfera}}{\rho_{agua}}V_{esfera} V_{sobreagua} = \Big( 1- \frac{\rho_{esfera}}{\rho_{agua}}\Big) V_{esfera} V_{esfera} = \frac{4}{3}\pi r^3 \frac{\pi h^2}{3}(3r-h) = \Big( 1- \frac{\rho_{esfera}}{\rho_{agua}}\Big) \frac{4}{3}\pi r^3 h^2(3r-h) = \Big( 1- \frac{\rho_{esfera}}{\rho_{agua}}\Big) 4 r^3

El planteamiento para la búsqueda de raíces es f(x) = 0, que para este caso será:

f(h) = h^2(3r-h) - \Big( 1 - \frac{\rho_{esfera}}{\rho_{agua}}\Big) 4 r^3 = 0

usando los valores dados para el ejercicio, r=1 y ρ_esfera = 200 Kg/m³ y ρ_agua    = 1000 kg/m³ se tiene que:

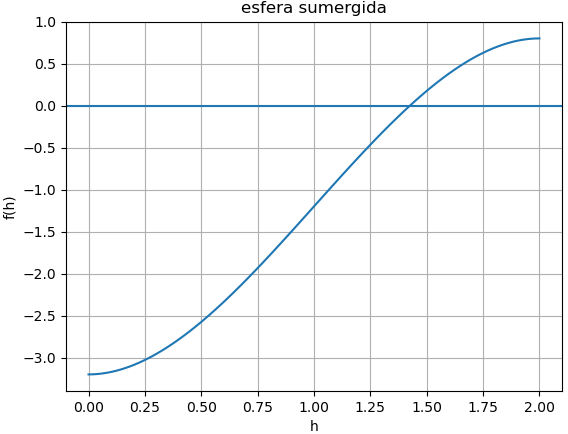
f(h) = h^2(3-h) - \Big( 1 - \frac{200}{1000}\Big) 4 f(h) = h^2(3-h) - \frac{16}{5}

Se observa la gráfica de f(h) en el intervalo de h entre[0,2] interpretado como totalmente sumergida y totalmente flotando sobre el agua, confirmando que existe una raíz

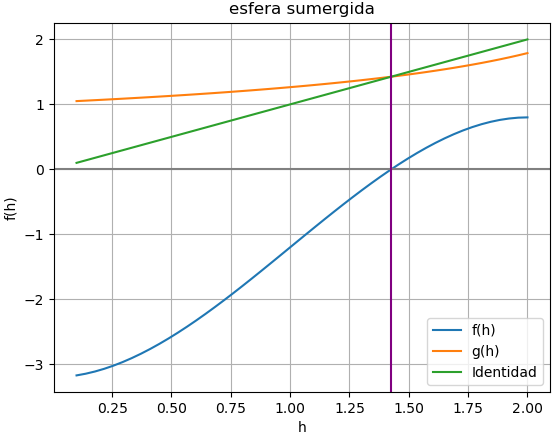
Para el caso de aplicar el método del punto fijo se plantea que x=g(x),

h = g(h) h^2(3-h) = \frac{16}{5}

con lo que se puede plantear dos ecuaciones al despejar h

h = \sqrt{ \frac{16}{5(3-h)}} h = 3-\frac{16}{5 h^2}

Iteraciones de la primera ecuación

itera = 0 ; h = h₀ = 0.5 ;

g(h) = \sqrt{ \frac{16}{5(3-0.5)}} = 1.1313 tramo = |1.1313-0.5|=0.6313

itera = 1 ; h = 1.1313 ;

g(h) = \sqrt{ \frac{16}{5(3-1.1313)}} = 1.3086 tramo = |1.3086-1.1313| = 0.1772

itera = 2 ; h = 1.3086 ;

g(h) = \sqrt{ \frac{16}{5(3-1.3086)}} = 1.3754 tramo = |1.3754-1.3086| = 0.0668

Observando los errores o tramos en cada iteración se tiene que se reduce, el método converge.

---

resultados.txt

x,g(x),tramo
0.5 1.131370849898476 0.631370849898476
1.131370849898476 1.308619626317284 0.17724877641880799
1.308619626317284 1.3754802083033437 0.06686058198605971
1.3754802083033437 1.4035002223557855 0.02802001405244181
1.4035002223557855 1.4157629993958152 0.012262777040029649
1.4157629993958152 1.4212317895316 0.005468790135784829
1.4212317895316 1.4236912066694054 0.0024594171378053975
1.4236912066694054 1.424801422465215 0.0011102157958096104
1.424801422465215 1.4253034412081806 0.0005020187429656264
raiz: 1.4253034412081806

Algoritmo en Python

# Algoritmo de punto fijo
# [a,b] intervalo de búsqueda
# error = tolera

import numpy as np
import matplotlib.pyplot as plt

def puntofijo(gx,a,tolera, iteramax = 15):
    i = 1 # iteración
    b = gx(a)
    tramo = abs(b-a)
    print('x,g(x),tramo')
    print(a,b,tramo)
    while(tramo>=tolera and i<=iteramax ):
        a = b
        b = gx(a)
        tramo = abs(b-a)
        print(a,b,tramo)
        i = i + 1
    respuesta = b
    
    # Validar respuesta
    if (i>=iteramax ):
        respuesta = np.nan
    return(respuesta)

# PROGRAMA ---------
# INGRESO
fx = lambda h: h**2*(3-h)-16/5
gx = lambda h: np.sqrt(16/(5*(3-h)))

#fx = lambda h: h**2*(3-h)-16/5
#gx = lambda h: 3-16/(5*(h**2))

x0 = 0.5
tolera = 0.001
iteramax = 50  # itera máximo
a = 0     # intervalo
b = 2
muestras = 51  # gráfico

# PROCEDIMIENTO
respuesta = puntofijo(gx,x0,tolera)

# SALIDA
print('raiz:',respuesta)

hi = np.linspace(a,b,muestras)
fi = fx(hi)
gi = gx(hi)
plt.plot(hi,fi,label='f(h)')
plt.plot(hi,gi,label='g(h)')
plt.plot(hi,hi,label='Identidad')
plt.axhline(0,color='grey')
plt.grid()
plt.xlabel('h')
plt.ylabel('f(h)')
plt.title('esfera sumergida')
plt.legend()
plt.show()