Ejercicio: 1Eva_2022PAOII_T3 Trayectoria de dron con polinomios
La variable independiente para la trayectoria es tiempo, con datos en el vector de ti.
ti = [0, 1, 2, 3, 4] xti = [2, 1, 3, 4, 2] yti = [0, 1, 5, 1, 0]
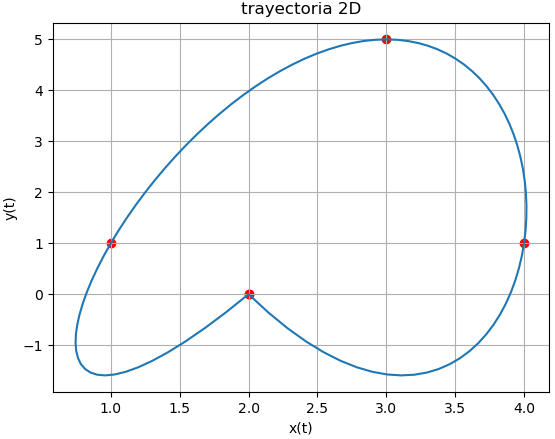
Considerando que los puntos marcan posiciones por donde debe pasar el dron y se define la trayectoria, se usarán todos los puntos. Cada polinomio será de grado 4 al incluir los 5 puntos disponibles para cada eje.
Nota: podría usar polinomios de menor grado, siempre que considere que se debe completar la trayectoria y regresar al punto de salida.
px(t) = 2\frac{(t-1)(t-2)(t-3)(t-4)}{(0-1)(0-2)(0-3)(0-4)} + 1 \frac{(t-0)(t-2)(t-3)(t-4)}{(1-0)(1-2)(1-3)(1-4)} + 3 \frac{(t-0)(t-1)(t-3)(t-4)}{(2-0)(2-1)(2-3)(2-4)} + 4 \frac{(t-0)(t-1)(t-2)(t-4)}{(3-0)(3-1)(3-2)(3-4)} + 2 \frac{(t-0)(t-1)(t-2)(t-3)}{(4-0)(4-1)(4-2)(4-3)}simplificando con el algoritmo:
px(t) = \frac{1}{12}t^4 - \frac{7}{6}t^3 + \frac{53}{12}t^2 - \frac{13}{3}t + 2Realizando lo mismo con el algoritmo para polinomio de Lagrange se obtiene:
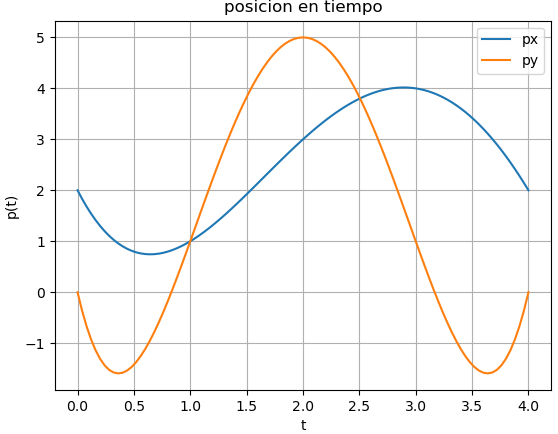
py(t) = \frac{11}{12}t^4 - \frac{22}{3}t^3 + \frac{205}{12}t^2 - \frac{29}{3}tse muestra la gráfica de trayectorias por cada eje vs tiempo
Observaciones: La trayectoria usada tiene el mismo punto de salida como de retorno. La trayectoria presenta lóbulos que podrían ser reducidos y minimizar uso de recursos como bateria. Considere usar trazadores cúbicos y observe la misma gráfica de trayectorias x(t) vs y(t).
Resultado con el algoritmo:
Polinomio de Lagrange x: x**4/12 - 7*x**3/6 + 53*x**2/12 - 13*x/3 + 2 Polinomio de Lagrange y: 11*x**4/12 - 22*x**3/3 + 205*x**2/12 - 29*x/3
Algoritmo en Python
# Interpolacion de Lagrange # divisoresL solo para mostrar valores import numpy as np import sympy as sym import matplotlib.pyplot as plt # INGRESO , Datos de prueba ti = [0,1,2,3,4] xti = [2,1,3,4,2] yti = [0,1,5,1,0] # PROCEDIMIENTO x = sym.Symbol('x') def interpola_lagrange(xi,yi): ''' Interpolación con método de Lagrange resultado: polinomio en forma simbólica ''' # PROCEDIMIENTO n = len(xi) x = sym.Symbol('x') # Polinomio polinomio = 0 for i in range(0,n,1): # Termino de Lagrange termino = 1 for j in range(0,n,1): if (j!=i): termino = termino*(x-xi[j])/(xi[i]-xi[j]) polinomio = polinomio + termino*yi[i] # Expande el polinomio polinomio = polinomio.expand() return(polinomio) # para ejex polinomiox = interpola_lagrange(ti,xti) polisimplex = polinomiox.expand() px = sym.lambdify(x,polisimplex) # para ejey polinomioy = interpola_lagrange(ti,yti) polisimpley = polinomioy.expand() py = sym.lambdify(x,polisimpley) # Puntos para la gráfica muestras = 101 a = np.min(ti) b = np.max(ti) ti = np.linspace(a,b,muestras) pxi = px(ti) pyi = py(ti) # SALIDA print('Polinomio de Lagrange x: ') print(polisimplex) print('Polinomio de Lagrange y: ') print(polisimpley) # Gráfica figura, enplano = plt.subplots() plt.scatter(xti,yti, color='red') plt.plot(pxi,pyi) plt.ylabel('y(t)') plt.xlabel('x(t)') plt.title('trayectoria 2D') plt.grid() figura, entiempo = plt.subplots() plt.plot(ti,pxi, label = 'px') plt.plot(ti,pyi, label = 'py') plt.legend() plt.title('posicion en tiempo') plt.xlabel('t') plt.ylabel('p(t)') plt.grid() plt.show()