Ejercicio: 1Eva_IIT2007_T1 Distribución binomial acumulada
Dado F=0.4, dado que n=5 y k=1
F = \sum_{t=0}^{k} \binom{n}{t} p^t (1-p)^{n-t}La fórmula para el ejercicio se convierte en:
F = \Bigg( \begin{array}{c} 5 \\ 0 \end{array} \Bigg) p ^0 (1-p)^{(5-0)} + \Bigg( \begin{array}{c} 5 \\ 1 \end{array} \Bigg) p ^1 (1-p)^{(5-1)} = 0.4Los valores de las combinatorias se calculan como:
>>> import scipy.special as sts >>> sts.comb(5,0,repetition=False) 1.0 >>> sts.comb(5,1,repetition=False) 5.0 >>>(1-p)^{5} + 5p (1-p)^{4} = 0.4
La expresión para el ejercicio se convierte en:
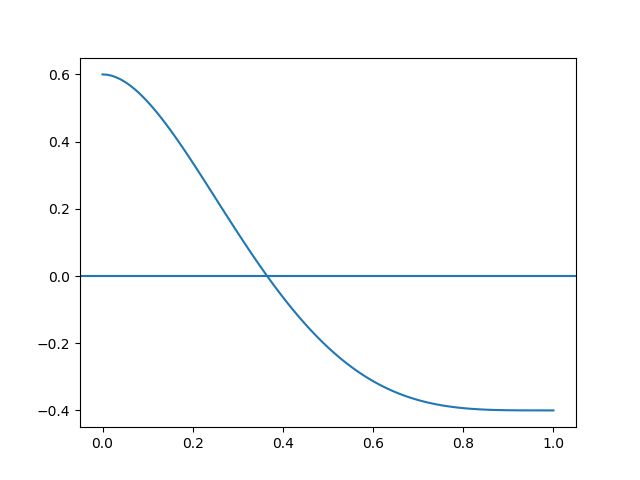
f(p) = (1-p)^{5} + 5p (1-p)^{4} - 0.4como referencia se revisa la gráfica para f(p)
y su derivada:
f'(p) = - 20p + 60p^2 + 60p^3 +20p^4con lo que se puede desarrollar el método Newton-Raphson.
Verificando el polinomio obtenido a partir de la expresión inicial usando Sympy:
>>> import sympy as sp
>>> p = sp.Symbol('p')
>>> poli = (1-p)**5 + 5*p*((1-p)**4) - 0.4
>>> pol = poli.expand()
>>> pol
4*p**5 - 15*p**4 + 20*p**3 - 10*p**2 + 0.6
>>> pol.diff(p,1)
20*p**4 - 60*p**3 + 60*p**2 - 20*p
A partir de la gráfica, un punto inicial cercano a la raíz es X0 = 0.2
itera = 0
f(0.2) = 0.6 - 10(0.2)^2 + 20(0.2)^3 + 15(0.2)^4 + 4(0.2)^5 = 0.3373 f'(0.2) = - 20(0.2) + 60(0.2)^2 + 60(0.2)^3 +20(0.2)^4 = -2.048 x_1 = 0.2 -\frac{0.3373}{-2.048} = 0.3647 errado = |0.2 - 0.36469| = 0.1647itera = 1
f(0.36469) = 0.6 - 10(0.36469)^2 + 20(0.36469)^3 + 15(0.36469)^4 + 4(0.36469)^5 = 0.0005566 f'(0.36469) = - 20(0.36469) + 60(0.36469)^2 + 60(0.36469)^3 +20(0.36469)^4 = -1.8703 x_1 = 0.36469 -\frac{0.0005566}{-1.8703} = 0.36499 errado = |0.36469 - 0.36499| = 0.000297itera = 3
f(0.36499) = 0.6 - 10(0.36499)^2 + 20(0.36499)^3 + 15(0.36499)^4 + 4(0.36499)^5 = 1.6412291237166698e-07 f'(0.36499) = - 20(0.36499) + 60(0.36499)^2 + 60(0.36499)^3 +20(0.36499)^4 = -1.869204616112814 x_1 = 0.36469 -\frac{1.6412291237166698e-07}{ -1.8692} = 0.36499 errado = |0.36499 - 0.36499| = 8.7804e-08verificar con raíz: 0.3649852264049102
Instrucciones para la gráfica
# 1ra Eval II Término 2007 # Tema 1. Distribución binomial acumulada import numpy as np import matplotlib.pyplot as plt import scipy.special as sts fp = lambda p: (1-p)**5 + 5*p*((1-p)**4) - 0.4 a = 0 b = 1 pasos = 100 # PROCEDIMIENTO xi = np.linspace(a,b,pasos+1) p_i = fp(xi) # SALIDA plt.plot(xi,p_i) plt.axhline(0) plt.show()
Algoritmo en Python
el resultado usando el algoritmo es:
i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo'] 0 [ 0.2 0.3373 -2.048 0.3647 0.1647] 1 [ 3.6469e-01 5.5668e-04 -1.8703e+00 3.6499e-01 2.9764e-04] 2 [ 3.6499e-01 1.6412e-07 -1.8692e+00 3.6499e-01 8.7804e-08] raiz en: 0.3649852264049102
con error de: 8.780360960525257e-08
Instrucciones en Python para Newton-Raphson
# 1Eva_IIT2007_T1 Distribución binomial acumulada # Método de Newton-Raphson import numpy as np import matplotlib.pyplot as plt def newton_raphson(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4): ''' fx y dfx en forma numérica lambda xi es el punto inicial de búsqueda ''' itera=0 tramo = abs(2*tolera) if vertabla==True: print('método de Newton-Raphson') print('i', ['xi','fi','dfi', 'xnuevo', 'tramo']) np.set_printoptions(precision) while (tramo>=tolera): fi = fx(xi) dfi = dfx(xi) xnuevo = xi - fi/dfi tramo = abs(xnuevo-xi) if vertabla==True: print(itera,np.array([xi,fi,dfi,xnuevo,tramo])) xi = xnuevo itera = itera + 1 if itera>=iteramax: xi = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') return(xi) # INGRESO fx = lambda p: 4*p**5 - 15*p**4 + 20*p**3 - 10*p**2 + 0.6 dfx = lambda p: 20*p**4 - 60*p**3 + 60*p**2 - 20*p x0 = 0.2 tolera = 0.0000001 # PROCEDIMIENTO respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True) # SALIDA print('raiz en: ', respuesta) # GRAFICA a = 0 b = 1 muestras = 21 xi = np.linspace(a,b,muestras) fi = fx(xi) plt.plot(xi,fi, label='f(x)') plt.axhline(0) plt.xlabel('x') plt.ylabel('f(x)') plt.grid() plt.legend() plt.show()