Ejercicio: 1Eva_IIT2007_T2 Aplicar Gauss-Seidel 6×6
1. Desarrollo Analítico
– Verificar que la matriz es diagonal dominante
No es necesario realizar el pivoteo por filas, ya la matriz tiene la diagonal dominante.
A = [[7.63, 0.30, 0.15, 0.50, 0.34, 0.84],
[0.38, 6.40, 0.70, 0.90, 0.29, 0.57],
[0.83, 0.19, 8.33, 0.82, 0.34, 0.37],
[0.50, 0.68, 0.86, 10.21, 0.53, 0.70],
[0.71, 0.30, 0.85, 0.82, 5.95, 0.55],
[0.43, 0.54, 0.59, 0.66, 0.31, 9.25]]
B = [ -9.44, 25.27, -48.01, 19.76, -23.63, 62.59]
– revisar el número de condición
cond(A) = || A||.||A-1||
El número de condición no es «muy alto», los valores de la diagonal son los mayores en toda la fila, por lo que el sistema converge.
>>> np.linalg.cond(A) 2.04518539662910119
– realizar iteraciones con las expresiones:
x_0 = \Big(-9.44 -0.3 x_1 -0.15x_2 -0.50 x_3 -0.34 x_4 -0.84 x_5\Big)\frac{1}{7.63} x_1 = \Big( 25.27 -0.38 x_0 -0.70 x_2 -0.90 x_3 -0.29 x_4 -0.57 x_5 \Big) \frac{1}{6.40} x_2 = \Big(-48.01 -0.83x_0 -0.19 x_1 -0.82x_3 -0.34x_4 -0.37x_5 \Big)\frac{1}{8.33} x_3 = \Big(19.76 -0.50 x_0 -0.68 x_1 -0.86 x_2 -0.53 x_4 -0.70x_5 \Big)\frac{1}{10.21} x_4 = \Big( -23.63 - 0.71 x_0 -0.30 x_1 -0.85 x_2 -0.82 x_3 -0.55x_5 \Big)\frac{1}{5.95} x_5 = \Big( 62.59 - 0.43x_0 -0.54x_1 - 0.59 x_2 -0.66 x_3 -0.31 x_4 \Big)\frac{1}{9.25}Dado que no se establece en el enunciado el vector inicial, se usará el vector cero. La tolerancia requerida es 10-5
X0 = [ 0. 0. 0. 0. 0. 0.] = [x0,x1,x2,x3,x4,x5]
iteración 0
x_0 = \Big(-9.44 -0.3 (0) -0.15(0) -0.50 (0) -0.34(0) -0.84 (0)\Big)\frac{1}{7.63} = -1.23722 x_1 = \Big( 25.27 -0.38 (-1.23722) -0.70 (0) -0.90 (0) -0.29 (0) -0.57 (0) \Big) \frac{1}{6.40} = 4.0219 x_2 = \Big(-48.01 -0.83 (-1.23722) -0.19 (4.0219) -0.82(0) -0.34(0) -0.37(0) \Big)\frac{1}{8.33} = -5.73196 x_3 = \Big( 19.76 -0.50 (-1.23722) -0.68 (4.0219) -0.86 (-5.73196) -0.53 (0) -0.70(0) \Big)\frac{1}{10.21} = 2.21089 x_4 = \Big( -23.63 - 0.71 (-1.23722) -0.30 (4.0219) -0.85 (-5.73196) -0.82 (2.21089) -0.55(0) \Big)\frac{1}{5.95} = -3.51242 x_5 = \Big( 62.59 - 0.43(-1.23722) -0.54(4.0219) - 0.59 (-5.73196) -0.66 (2.21089) -0.31 (-3.51242) \Big)\frac{1}{9.25} = 6.91478 X_1 = [-1.23722, 4.0219, -5.73196, 2.21089, -3.51242, 6.91478 ] diferencia = X1 - [0,0,0,0,0,0] errado = max(|diferencia|) = 6.91478iteración 1
x_0 = \Big(-9.44 -0.3 (4.0219) -0.15(4.0219) -0.50 (2.21089) -0.34 (-3.51242) -0.84(6.91478) \Big)\frac{1}{7.63} = -2.0323 x_1 = \Big( 25.27 -0.38 (-2.0323) -0.70 ( -5.73196) -0.90 (2.21089) -0.29 (-3.51242) -0.57 (6.91478) \Big) \frac{1}{6.40} = 3.92844 x_2 = \Big(-48.01 -0.83(-2.0323) -0.19 (3.92844) -0.82(2.21089) -0.34(-3.51242) -0.37(6.91478) \Big)\frac{1}{8.33} = -6.03203 x_3 = \Big(19.76 -0.50 (-2.0323) -0.68 (3.92844) -0.86 (-6.03203) -0.53 (-3.51242) -0.70(6.91478) \Big)\frac{1}{10.21} = 1.98958 x_4 = \Big( -23.63 - 0.71 (-2.0323) -0.30 (3.92844) -0.85 (-6.03203) -0.82 (1.98958) -0.55(6.91478) \Big)\frac{1}{5.95} = -3.97865 x_5 = \Big( 62.59 - 0.43(-2.0323) -0.54(3.92844) - 0.59 (-6.03203) -0.66 (1.98958) -0.31 (-3.97865) \Big)\frac{1}{9.25} = 7.00775 X_2 = [-2.0323, 3.92844, -6.03203, 1.98958, -3.97865, 7.00775] diferencia = X2 - [-1.23722, 4.0219, -5.73196, 2.21089, -3.51242, 6.91478 ] errado = max(|diferencia|) = 0.79507iteración 2
Desarrollar como tarea.
2. Algoritmo en Python
La tabla de aproximaciones sucesivas para el vector X es:
Pivoteo por filas NO requerido Iteraciones Gauss-Seidel itera,[X],[errado] 0 [0. 0. 0. 0. 0. 0.] [1.] 1 [-1.23722 4.0219 -5.73196 2.21089 -3.51242 6.91478] [6.91478] 2 [-2.0323 3.92844 -6.03203 1.98958 -3.97865 7.00775] [0.79507] 3 [-1.99768 4.00317 -6.00049 1.99808 -4.00082 6.9999 ] [0.07473] 4 [-1.99994 4.00037 -5.99979 2. -4.00005 6.99996] [0.00281] 5 [-2.00001 3.99998 -6. 2.00001 -4. 7. ] [0.00038] 6 [-2. 4. -6. 2. -4. 7.] [1.60155e-05] 7 [-2. 4. -6. 2. -4. 7.] [1.74554e-06] Matriz aumentada y pivoteada: [[ 7.63 0.3 0.15 0.5 0.34 0.84 -9.44] [ 0.38 6.4 0.7 0.9 0.29 0.57 25.27] [ 0.83 0.19 8.33 0.82 0.34 0.37 -48.01] [ 0.5 0.68 0.86 10.21 0.53 0.7 19.76] [ 0.71 0.3 0.85 0.82 5.95 0.55 -23.63] [ 0.43 0.54 0.59 0.66 0.31 9.25 62.59]] Vector Xi: [-2. 4. -6. 2. -4. 7.] >>>
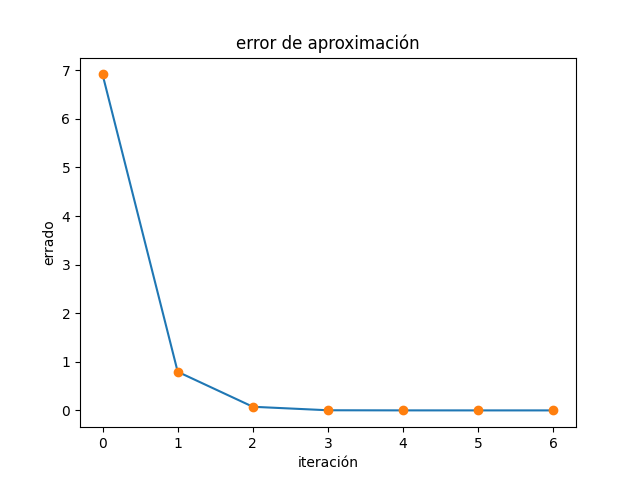
el gráfico de los iteraciones vs errores es:
La tabla obtiene aplicando la función de Gauss-Seidel, tomando como vector inicial el vector de ceros.
Tarea: X=TX+C
Instrucciones en Python
# 1Eva_IIT2007_T2 Aplicar Gauss-Seidel # Algoritmo Gauss-Seidel import numpy as np def pivoteafila(A,B,vertabla=False): ''' Pivotea parcial por filas Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) M = np.copy(AB) # Pivoteo por filas AB tamano = np.shape(M) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(M[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(M[i,:]) M[i,:] = M[dondemax+i,:] M[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(pivoteado, 'intercambiar: ',i,dondemax) if vertabla==True and pivoteado==0: print('Pivoteo por filas NO requerido') return(M) def gauss_seidel(A,B,tolera,X0, iteramax=100, vertabla=False, precision=5): ''' Método de Gauss Seidel, tolerancia, vector inicial X0 para mostrar iteraciones: vertabla=True ''' tamano = np.shape(A) n = tamano[0] m = tamano[1] diferencia = 2*tolera*np.ones(n, dtype=float) errado = np.max(diferencia) X = np.copy(X0) itera = 0 if vertabla==True: print('Iteraciones Gauss-Seidel') print('itera,[X],[errado]') np.set_printoptions(precision) print(itera, X, np.array([errado])) while (errado>tolera and itera<iteramax): for i in range(0,n,1): xi = B[i] for j in range(0,m,1): if (i!=j): xi = xi-A[i,j]*X[j] xi = xi/A[i,i] diferencia[i] = np.abs(xi-X[i]) X[i] = xi errado = np.max(diferencia) itera = itera + 1 if vertabla==True: print(itera, X, np.array([errado])) if (itera>iteramax): # No converge X = itera print('iteramax superado, No converge') return(X) # Programa de prueba ####### # INGRESO A = np.array([[7.63, 0.30, 0.15, 0.50, 0.34, 0.84], [0.38, 6.40, 0.70, 0.90, 0.29, 0.57], [0.83, 0.19, 8.33, 0.82, 0.34, 0.37], [0.50, 0.68, 0.86, 10.21, 0.53, 0.70], [0.71, 0.30, 0.85, 0.82, 5.95, 0.55], [0.43, 0.54, 0.59, 0.66, 0.31, 9.25]]) B = np.array([-9.44,25.27,-48.01,19.76,-23.63,62.59]) tolera = 0.00001 X = np.zeros(len(A), dtype=float) # PROCEDIMIENTO n = len(A) A = np.array(A,dtype=float) B = np.array(B,dtype=float) AB = pivoteafila(A,B, vertabla=True) A = AB[:,:n] B = AB[:,n] respuesta = gauss_seidel(A,B, tolera, X, vertabla=True) # SALIDA print('Matriz aumentada y pivoteada:') print(AB) print('Vector Xi: ') print(respuesta)
En el caso de la norma infinito, para la matriz A, se puede usar el algoritmo desarrollado en clase.
Como valor para verificar su algoritmo, se obtuvo:
>>> np.linalg.norm(A, np.inf) 13.479999999999999
Tarea: incluir la norma infinito para T