s1Eva_IIT2007_T3 Interpolación inversa, encontrar xi para fi dado

Ejercicio: 1Eva_IIT2007_T3 Interpolación inversa

Para determinar el valor de x, usando interpolación inversa.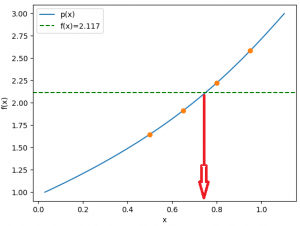

f(0.50) = 1.648
f(0.65) = 1.915
f( x  ) = 2.117
f(0.80) = 2.225
f(0.95) = 2.5857

Para el algoritmo se intercambian las variables previo a usarlo.

fi = [0.50 , 0.65 , 0.80,  0.95   ]
xi = [1.648, 1.915, 2.225, 2.5857 ]

Luego se evalúa en el punto buscado, en éste caso: fi=2.117, obteniendo que x es: 0.750321134121361

Para obtener el polinomio se usa el método de Lagrange:

término 1

L_{0} (x) = \frac{(x-1.915)(x-2.225)(x-2.5857)}{(1.648-1.915)(1.648-2.225)(1.648-2.5857)}

término 2

L_{1} (x) = \frac{(x-1.648)(x-2.225)(x-2.5857)}{(1.915-1.648)(1.915-2.225)(1.915-2.5857)}

término 3

L_{2} (x) = \frac{(x-1.648)(x-1.915)(x-2.5857)}{(2.225-1.648)(2.225-1.915)(2.225-2.5857)}

término 4

L_{3} (x) = \frac{(x-1.648)(x-1.915)(x-2.225)}{(2.5857-1.648)(2.5857-1.915)(2.5857-2.225)}

se construye el polinomio usando la fórmula para f_n(x) para cada valor fi,

p_3(x) = 0.5 L_{0} (x) + 0.65 L_{1} (x) + 0.8 L_{2} (x) + 0.95 L_{3} (x) p_3(x) = 0.5 \frac{(x-1.915)(x-2.225)(x-2.5857)}{-0.14446112} + +0.65 \frac{(x-1.648)(x-2.225)(x-2.5857)}{0.05551384 } + + 0.8 \frac{(x-1.648)(x-1.915)(x-2.5857)}{-0.06451841} + +0.95 \frac{(x-1.648)(x-1.915)(x-2.225)}{0.22684978} p_3(x) = 0.03588 x^3 - 0.34275 x^2 + 1.44073 x - 1.10404

A partir del resultado del algoritmo se puede evaluar p(2.117)

    valores de fi:  [0.5  0.65 0.8  0.95]
divisores en L(i):  [-0.14446112  0.05551384 -0.06451841  0.22684978]

Polinomio de Lagrange, expresiones
-3.46113878334255*(x - 2.5857)*(x - 2.225)*(x - 1.915) 
+ 11.7087921085767*(x - 2.5857)*(x - 2.225)*(x - 1.648) 
- 12.3995618056856*(x - 2.5857)*(x - 1.915)*(x - 1.648) 
+ 4.18779332775953*(x - 2.225)*(x - 1.915)*(x - 1.648)

Polinomio de Lagrange: 
0.0358848473081546*x**3 - 0.342756582990933*x**2 
+ 1.44073214117569*x - 1.10404634485234
>>> polisimple.subs(x,2.117)
0.750321134121178
>>> polisimple
0.0358848473081546*x**3 - 0.342756582990933*x**2 
+ 1.44073214117569*x - 1.10404634485234
>>> 

---

Algoritmo en Python

# 1Eva_IIT2007_T3 Interpolación inversa
# Interpolacion de Lagrange
# divisoresL solo para mostrar valores
import numpy as np
import matplotlib.pyplot as plt
import sympy as sym

# INGRESO , Datos de prueba
fi = [0.50 , 0.65 , 0.80,  0.95   ]
xi = [1.648, 1.915, 2.225, 2.5857 ]

# PROCEDIMIENTO
xi = np.array(xi,dtype=float)
fi = np.array(fi,dtype=float)
# Polinomio de Lagrange
n = len(xi)
x = sym.Symbol('x')
polinomio = 0
divisorL = np.zeros(n, dtype = float)
for i in range(0,n,1):
    
    # Termino de Lagrange
    numerador = 1
    denominador = 1
    for j  in range(0,n,1):
        if (j!=i):
            numerador = numerador*(x-xi[j])
            denominador = denominador*(xi[i]-xi[j])
    terminoLi = numerador/denominador

    polinomio = polinomio + terminoLi*fi[i]
    divisorL[i] = denominador

# simplifica el polinomio
polisimple = polinomio.expand()

# Salida
print('    valores de fi: ',fi)
print('divisores en L(i): ',divisorL)
print()
print('Polinomio de Lagrange, expresiones')
print(polinomio)
print()
print('Polinomio de Lagrange: ')
print(polisimple)

para revisar con la gráfica, se añaden las líneas,

# GRAFICA
polinomio = sym.lambdify(x,polisimple)
y = np.linspace(1,3,100)
pyi= polinomio(y)
plt.plot(pyi,y,label='p(x)')
plt.plot(fi,xi,'o')
plt.axhline(2.117,linestyle='dashed',
            label='f(x)=2.117', color='green')
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()