Ejercicio: 1Eva_IIT2008_T1_MN Bacterias contaminantes

a. Planteamiento del problema

estandarizar la fórmula a la forma f(x) = 0

c = 70 e^{-1.5t} + 25 e^{-0.075t}

el valor que debe tomar c = 9, por lo que la función a desarrollar se convierte en:

9 = 70 e^{-1.5t} + 25 e^{-0.075t}

y la que se usará en el algoritmo de búsqueda de raices es:

70 e^{-1.5t} + 25 e^{-0.075t} -9 = 0

f(t) = 70 e^{-1.5t} + 25 e^{-0.075t} -9 = 0

b. Intervalo de búsqueda [a,b]

Como la variable t representa el tiempo, se inicia el análisis con cero por la izquierda o un poco mayor. a=0

Para verificar que existe raíz se evalua f(a) y f(b) buscando valores donde se presenten cambios de signo.

La función depende de tiempo, por lo que a = 0, y b seleccionar un valor mayor.

Para el caso de b, si fuesen minutos, se pueden probar con valores consideranto el tiempo que duraría un «experimento» en el laboratorio durante una clase. Por ejemplo 60 minutos, 30 minutos, etc, para obtener un punto «b» donde se garantice un cambio de signo f(a) y f(b)

Para el ejemplo, se prueba con b = 15

a = 0
b = 15
f(a) = f(0) = 70*e⁰ + 25 e⁰ -9 = 86
f(b) = f(15) = 70*e^-1.5*15. + 25 e^-0.075*15 -9 = - 0.0036

c. Número de iteraciones

Calcular el número de iteraciones para llegar a la raíz con el error tolerado

error = 0.001

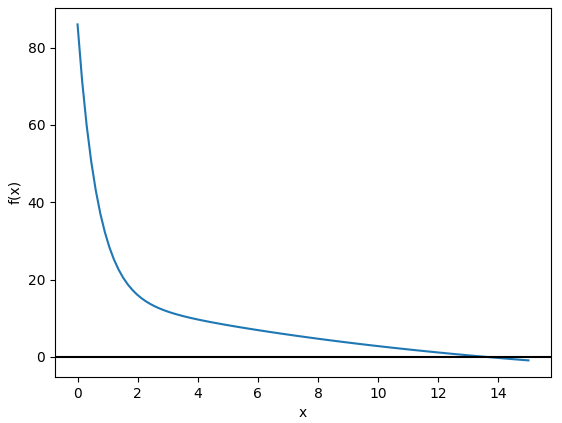
\frac{|15-0|}{2^n} = 0.001

15/0.001 = 2^n

log(15/0.001) = nlog(2)

n = \frac{log(15/0.001)}{log(2)} = 13.87

n = 14

Verificando la selección usando una gráfica, usando 50 tramos entre [a,b] o 51 muestras en el rango.

d. Calcular la raíz:

Usando el algoritmo se encuentra que la raiz está en:

raiz en:  13.62213134765625
f(raiz) = -7.733799068e-05

si realiza la tabla:

[i,a,b,c,sign(fa),sign(fb),sign(fc),paso]
[[1, 0, 15, 7.5, 1.0, -1.0, 1.0, 15], 
 [2, 7.5, 15, 11.25, 1.0, -1.0, 1.0, 7.5], 
 [3, 11.25, 15, 13.125, 1.0, -1.0, 1.0, 3.75], 
 [4, 13.125, 15, 14.0625, 1.0, -1.0, -1.0, 1.875], 
 [5, 13.125, 14.0625, 13.59375, 1.0, -1.0, 1.0, 0.9375], 
 [6, 13.59375, 14.0625, 13.828125, 1.0, -1.0, -1.0, 0.46875], 
 [7, 13.59375, 13.828125, 13.7109375, 1.0, -1.0, -1.0, 0.234375], 
 [8, 13.59375, 13.7109375, 13.65234375, 1.0, -1.0, -1.0, 0.1171875], 
 [9, 13.59375, 13.65234375, 13.623046875, 1.0, -1.0, -1.0, 0.05859375], 
 [10, 13.59375, 13.623046875, 13.6083984375, 1.0, -1.0, 1.0, 0.029296875],
 [11, 13.6083984375, 13.623046875, 13.61572265625, 1.0, -1.0, 1.0, 0.0146484375], 
 [12, 13.61572265625, 13.623046875, 13.619384765625, 1.0, -1.0, 1.0, 0.00732421875], 
 [13, 13.619384765625, 13.623046875, 13.6212158203125, 1.0, -1.0, 1.0, 0.003662109375], 
 [14, 13.6212158203125, 13.623046875, 13.62213134765625, 1.0, -1.0, -1.0, 0.0018310546875]]

Cálculos con Newton – Raphson

Se encuentra la derivada f'(t) y se aplica el algoritmo Newton-Raphson con valor inicial cero.

f'(t) = 70(-1.5) e^{-1.5t} + 25(-0.075) e^{-0.075t}

raiz en:  13.622016772385583

Se usa el algoritmo en python para encontrar el valor. El algoritmo newton Raphson mostrado es más pequeño que por ejemplo la bisección, pero requiere realizar un trabajo previo para encontrar la derivada de la función.

# 1ra Eval II Termino 2008 tema 1
# Método de Newton-Raphson
import numpy as np

def newtonraphson(funcionx, fxderiva, c, tolera):
    tramo = abs(2*tolera)
    while (tramo>=tolera):
        xnuevo = c - funcionx(c)/fxderiva(c)
        tramo = abs(xnuevo-c)
        c = xnuevo
    return(c)


# PROGRAMA ---------------------------------
funcionx = lambda t: 70*(np.e**(-1.5*t)) +25*(np.e**(-0.075*t))-9
fxderiva = lambda t: -70*1.5*(np.e**(-1.5*t)) -25*0.075*(np.e**(-0.075*t))

# INGRESO
c = 0.1
tolera = 0.001

# PROCEDIMIENTO
raiz = newtonraphson(funcionx, fxderiva, c, tolera)

# SALIDA
print('raiz en: ', raiz)

# Gráfica
import matplotlib.pyplot as plt
xi = np.linspace(0,15,100)
yi = funcionx(xi)
plt.plot(xi,yi)
plt.axhline(0, color = 'k')
plt.show()

Tarea: Para el problema, realice varios métodos y compare el número de iteraciones y el trabajo realizado al plantear el problema al implementar cada uno.