Ejercicio : 1Eva_IIT2008_T3_MN Ganancia en inversión
Se dispone de los datos (x , f (x )), en donde x es un valor de inversión y f (x ) es un valor de ganancia, ambos en miles de dólares.
xi = np.array([3.2 , 3.8 , 4.2 , 4.5 ])
fi = np.array([5.12, 6.42, 7.25, 6.85])
Los datos se usan junto al modelo propuesto:
f ( x ) = a 1 x 3 + a 2 x 2 + a 3 x + a 4 f(x) = a_1 x^3 + a_2 x^2 + a_3 x + a_4 f ( x ) = a 1 x 3 + a 2 x 2 + a 3 x + a 4 generando las expresiones del sistema de ecuaciones:
a 1 ( 3 . 2 ) 3 + a 2 ( 3 . 2 ) 2 + a 3 ( 3 . 2 ) + a 4 = 5 . 1 2 a_1 (3.2)^3 + a_2 (3.2)^2 + a_3 (3.2) + a_4 = 5.12 a 1 ( 3 . 2 ) 3 + a 2 ( 3 . 2 ) 2 + a 3 ( 3 . 2 ) + a 4 = 5 . 1 2 a 1 ( 3 . 8 ) 3 + a 2 ( 3 . 8 ) 2 + a 3 ( 3 . 8 ) + a 4 = 6 . 4 2 a_1 (3.8)^3 + a_2 (3.8)^2 + a_3 (3.8) + a_4 = 6.42 a 1 ( 3 . 8 ) 3 + a 2 ( 3 . 8 ) 2 + a 3 ( 3 . 8 ) + a 4 = 6 . 4 2 a 1 ( 4 . 2 ) 3 + a 2 ( 4 . 2 ) 2 + a 3 ( 4 . 2 ) + a 4 = 7 . 2 5 a_1 (4.2)^3 + a_2 (4.2)^2 + a_3 (4.2) + a_4 = 7.25 a 1 ( 4 . 2 ) 3 + a 2 ( 4 . 2 ) 2 + a 3 ( 4 . 2 ) + a 4 = 7 . 2 5 a 1 ( 4 . 5 ) 3 + a 2 ( 4 . 5 ) 2 + a 3 ( 4 . 5 ) + a 4 = 6 . 8 5 a_1 (4.5)^3 + a_2 (4.5)^2 + a_3 (4.5) + a_4 = 6.85 a 1 ( 4 . 5 ) 3 + a 2 ( 4 . 5 ) 2 + a 3 ( 4 . 5 ) + a 4 = 6 . 8 5 Se convierte a la forma Ax=B[ ( 3 . 2 ) 3 ( 3 . 2 ) 2 ( 3 . 2 ) 1 ( 3 . 8 ) 3 ( 3 . 8 ) 2 ( 3 . 8 ) 1 ( 4 . 2 ) 3 ( 4 . 2 ) 2 ( 4 . 2 ) 1 ( 4 . 5 ) 3 ( 4 . 5 ) 2 ( 4 . 5 ) 1 ] . [ a 1 a 2 a 3 a 4 ] = [ 5 . 1 2 6 . 4 2 7 . 2 5 6 . 8 5 ] \begin{bmatrix} (3.2)^3 && (3.2)^2 && (3.2) && 1 \\ (3.8)^3 && (3.8)^2 && (3.8) && 1 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 \\ (4.5)^3 && (4.5)^2 && (4.5) && 1 \end{bmatrix} . \begin{bmatrix} a_1 \\ a_2 \\ a_3 \\ a_4 \end{bmatrix} = \begin{bmatrix} 5.12 \\ 6.42 \\ 7.25 \\6.85 \end{bmatrix} ⎣ ⎢ ⎢ ⎡ ( 3 . 2 ) 3 ( 3 . 8 ) 3 ( 4 . 2 ) 3 ( 4 . 5 ) 3 ( 3 . 2 ) 2 ( 3 . 8 ) 2 ( 4 . 2 ) 2 ( 4 . 5 ) 2 ( 3 . 2 ) ( 3 . 8 ) ( 4 . 2 ) ( 4 . 5 ) 1 1 1 1 ⎦ ⎥ ⎥ ⎤ . ⎣ ⎢ ⎢ ⎡ a 1 a 2 a 3 a 4 ⎦ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎡ 5 . 1 2 6 . 4 2 7 . 2 5 6 . 8 5 ⎦ ⎥ ⎥ ⎤
Se crea la matriz aumentada
[ ( 3 . 2 ) 3 ( 3 . 2 ) 2 ( 3 . 2 ) 1 5 . 1 2 ( 3 . 8 ) 3 ( 3 . 8 ) 2 ( 3 . 8 ) 1 6 . 4 2 ( 4 . 2 ) 3 ( 4 . 2 ) 2 ( 4 . 2 ) 1 7 . 2 5 ( 4 . 5 ) 3 ( 4 . 5 ) 2 ( 4 . 5 ) 1 6 . 8 5 ] \begin{bmatrix} (3.2)^3 && (3.2)^2 && (3.2) && 1 && 5.12\\ (3.8)^3 && (3.8)^2 && (3.8) && 1 && 6.42 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 && 7.25 \\ (4.5)^3 && (4.5)^2 && (4.5) && 1 && 6.85 \end{bmatrix} ⎣ ⎢ ⎢ ⎡ ( 3 . 2 ) 3 ( 3 . 8 ) 3 ( 4 . 2 ) 3 ( 4 . 5 ) 3 ( 3 . 2 ) 2 ( 3 . 8 ) 2 ( 4 . 2 ) 2 ( 4 . 5 ) 2 ( 3 . 2 ) ( 3 . 8 ) ( 4 . 2 ) ( 4 . 5 ) 1 1 1 1 5 . 1 2 6 . 4 2 7 . 2 5 6 . 8 5 ⎦ ⎥ ⎥ ⎤ Se pivotea por filas:
[ ( 4 . 5 ) 3 ( 4 . 5 ) 2 ( 4 . 5 ) 1 6 . 8 5 ( 4 . 2 ) 3 ( 4 . 2 ) 2 ( 4 . 2 ) 1 7 . 2 5 ( 3 . 8 ) 3 ( 3 . 8 ) 2 ( 3 . 8 ) 1 6 . 4 2 ( 3 . 2 ) 3 ( 3 . 2 ) 2 ( 3 . 2 ) 1 5 . 1 2 ] \begin{bmatrix} (4.5)^3 && (4.5)^2 && (4.5) && 1 && 6.85 \\ (4.2)^3 && (4.2)^2 && (4.2) && 1 && 7.25 \\ (3.8)^3 && (3.8)^2 && (3.8) && 1 && 6.42 \\ (3.2)^3 && (3.2)^2 && (3.2) && 1 && 5.12 \end{bmatrix} ⎣ ⎢ ⎢ ⎡ ( 4 . 5 ) 3 ( 4 . 2 ) 3 ( 3 . 8 ) 3 ( 3 . 2 ) 3 ( 4 . 5 ) 2 ( 4 . 2 ) 2 ( 3 . 8 ) 2 ( 3 . 2 ) 2 ( 4 . 5 ) ( 4 . 2 ) ( 3 . 8 ) ( 3 . 2 ) 1 1 1 1 6 . 8 5 7 . 2 5 6 . 4 2 5 . 1 2 ⎦ ⎥ ⎥ ⎤ Como se pide un método directo, se inicia con el algoritmo de eliminación hacia adelante con factor para cada fila a partir de la diagonal.
[ ( 4 . 5 ) 3 ( 4 . 5 ) 2 ( 4 . 5 ) ( 4 . 2 ) 3 − ( 4 . 5 ) 3 ( 4 . 2 ) 3 ( 4 . 5 ) 3 ( 4 . 2 ) 2 − ( 4 . 5 ) 2 ( 4 . 2 ) 3 ( 4 . 5 ) 3 ( 4 . 2 ) − ( 4 . 5 ) ( 4 . 2 ) 3 ( 4 . 5 ) 3 ( 3 . 8 ) 3 − ( 4 . 5 ) 3 ( 3 . 8 ) 3 ( 4 . 5 ) 3 ( 3 . 8 ) 2 − ( 4 . 5 ) 2 ( 3 . 8 ) 3 ( 4 . 5 ) 3 ( 3 . 8 ) − ( 4 . 5 ) ( 3 . 8 ) 3 ( 4 . 5 ) 3 ( 3 . 2 ) 3 − ( 4 . 5 ) 3 ( 3 . 2 ) 3 ( 4 . 5 ) 3 ( 3 . 2 ) 2 − ( 4 . 5 ) 2 ( 3 . 2 ) 3 ( 4 . 5 ) 3 ( 3 . 2 ) − ( 4 . 5 ) ( 3 . 2 ) 3 ( 4 . 5 ) 3 ] \begin{bmatrix} (4.5)^3 && (4.5)^2 && (4.5) \\ (4.2)^3 - (4.5)^3\frac{(4.2)^3}{(4.5)^3} && (4.2)^2 - (4.5)^2\frac{(4.2)^3}{(4.5)^3} && (4.2) - (4.5)\frac{(4.2)^3}{(4.5)^3} \\ (3.8)^3 - (4.5)^3\frac{(3.8)^3}{(4.5)^3} && (3.8)^2 - (4.5)^2\frac{(3.8)^3}{(4.5)^3} && (3.8) -(4.5)\frac{(3.8)^3}{(4.5)^3} \\ (3.2)^3 - (4.5)^3\frac{(3.2)^3}{(4.5)^3} && (3.2)^2 -(4.5)^2\frac{(3.2)^3}{(4.5)^3} && (3.2) - (4.5)\frac{(3.2)^3}{(4.5)^3} \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ ( 4 . 5 ) 3 ( 4 . 2 ) 3 − ( 4 . 5 ) 3 ( 4 . 5 ) 3 ( 4 . 2 ) 3 ( 3 . 8 ) 3 − ( 4 . 5 ) 3 ( 4 . 5 ) 3 ( 3 . 8 ) 3 ( 3 . 2 ) 3 − ( 4 . 5 ) 3 ( 4 . 5 ) 3 ( 3 . 2 ) 3 ( 4 . 5 ) 2 ( 4 . 2 ) 2 − ( 4 . 5 ) 2 ( 4 . 5 ) 3 ( 4 . 2 ) 3 ( 3 . 8 ) 2 − ( 4 . 5 ) 2 ( 4 . 5 ) 3 ( 3 . 8 ) 3 ( 3 . 2 ) 2 − ( 4 . 5 ) 2 ( 4 . 5 ) 3 ( 3 . 2 ) 3 ( 4 . 5 ) ( 4 . 2 ) − ( 4 . 5 ) ( 4 . 5 ) 3 ( 4 . 2 ) 3 ( 3 . 8 ) − ( 4 . 5 ) ( 4 . 5 ) 3 ( 3 . 8 ) 3 ( 3 . 2 ) − ( 4 . 5 ) ( 4 . 5 ) 3 ( 3 . 2 ) 3 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ continua a la derecha de la matriz:
[ 1 6 . 8 5 1 − 1 ( 4 . 2 ) 3 ( 4 . 5 ) 3 7 . 2 5 − 6 . 8 5 ( 4 . 2 ) 3 ( 4 . 5 ) 3 1 − 1 ( 3 . 8 ) 3 ( 4 . 5 ) 3 6 . 4 2 − 6 . 8 5 ( 3 . 8 ) 3 ( 4 . 5 ) 3 1 − 1 ( 3 . 2 ) 3 ( 4 . 5 ) 3 5 . 1 2 − 6 . 8 5 ( 3 . 2 ) 3 ( 4 . 5 ) 3 ] \begin{bmatrix} 1 && 6.85 \\ 1 - 1\frac{(4.2)^3}{(4.5)^3} && 7.25 - 6.85\frac{(4.2)^3}{(4.5)^3} \\ 1 -1\frac{(3.8)^3}{(4.5)^3} && 6.42 - 6.85\frac{(3.8)^3}{(4.5)^3}\\1 -1\frac{(3.2)^3}{(4.5)^3} && 5.12-6.85\frac{(3.2)^3}{(4.5)^3} \end{bmatrix} ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 1 1 − 1 ( 4 . 5 ) 3 ( 4 . 2 ) 3 1 − 1 ( 4 . 5 ) 3 ( 3 . 8 ) 3 1 − 1 ( 4 . 5 ) 3 ( 3 . 2 ) 3 6 . 8 5 7 . 2 5 − 6 . 8 5 ( 4 . 5 ) 3 ( 4 . 2 ) 3 6 . 4 2 − 6 . 8 5 ( 4 . 5 ) 3 ( 3 . 8 ) 3 5 . 1 2 − 6 . 8 5 ( 4 . 5 ) 3 ( 3 . 2 ) 3 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ [[91.125 20.25 4.5 1. 6.85 ]
[ 0. 1.176 0.541 0.186 1.680]
[ 0. 2.246 1.090 0.397 2.295]
[ 0. 2.958 1.581 0.640 2.656]]
Elimina hacia adelante
[[91.125 20.250 4.500 1.000 6.850]
[ 0. 1.176 0.541 0.186 1.680]
[ 0. 0. 0.056 0.040 -0.915]
[ 0. 0. 0.220 0.170 -1.571]]
Elimina hacia adelante
[[91.125 20.250 4.500 1.000 6.850]
[ 0. 1.176 0.541 0.186 1.680]
[ 0. 0.000 0.056 0.040 -0.915]
[ 0. 0.000 0.000 0.010 2.006]]
Elimina hacia adelante
[[91.125 20.250 4.500 1.000 6.850]
[ 0. 1.176 0.541 0.186 1.680]
[ 0. 0. 0.056 0.040 -0.915]
[ 0. 0. 0. 0.010 2.006]]
Elimina hacia atras
[[1. 0. 0. 0. -3.67490842]
[0. 1. 0. 0. 41.06730769]
[0. 0. 1. 0. -149.92086081]
[0. 0. 0. 1. 184.75692308]]
el vector solución X es:
[[ -3.67490842]
[ 41.06730769]
[-149.92086081]
[ 184.75692308]]
verificar que A.X = B
[[6.85]
[7.25]
[6.42]
[5.12]]
con lo que el polinomio buscado es:
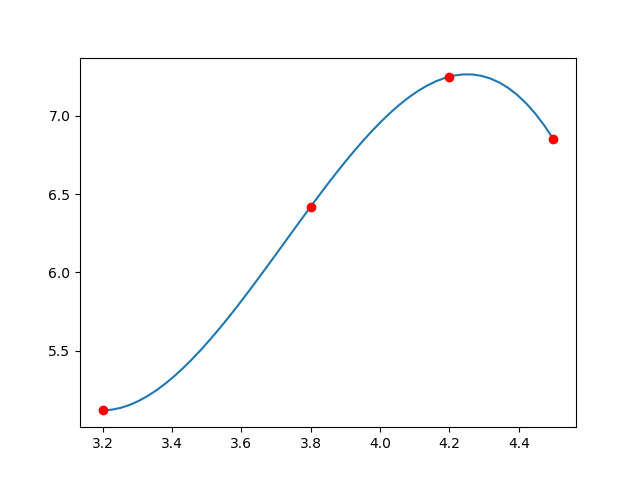
f ( x ) = − 3 . 6 7 4 9 0 8 4 2 x 3 + 4 1 . 0 6 7 3 0 7 6 9 x 2 + f(x) = -3.67490842 x^3 + 41.06730769 x^2 + f ( x ) = − 3 . 6 7 4 9 0 8 4 2 x 3 + 4 1 . 0 6 7 3 0 7 6 9 x 2 + − 1 4 9 . 9 2 0 8 6 0 8 1 x + 1 8 4 . 7 5 6 9 2 3 0 8 -149.92086081 x + 184.75692308 − 1 4 9 . 9 2 0 8 6 0 8 1 x + 1 8 4 . 7 5 6 9 2 3 0 8 que genera la siguiente gráfica:
para encontrar la cantidad necesaria a invertir y obtener 6.0 de ganancia en f(x):
6 . 0 = − 3 . 6 7 4 9 0 8 4 2 x 3 + 4 1 . 0 6 7 3 0 7 6 9 x 2 + 6.0 = -3.67490842 x^3 + 41.06730769 x^2 + 6 . 0 = − 3 . 6 7 4 9 0 8 4 2 x 3 + 4 1 . 0 6 7 3 0 7 6 9 x 2 + − 1 4 9 . 9 2 0 8 6 0 8 1 x + 1 8 4 . 7 5 6 9 2 3 0 8 -149.92086081 x + 184.75692308 − 1 4 9 . 9 2 0 8 6 0 8 1 x + 1 8 4 . 7 5 6 9 2 3 0 8 que para usar en el algoritmo se realiza se reordena como g(x) = 0
− 3 . 6 7 4 9 0 8 4 2 x 3 + 4 1 . 0 6 7 3 0 7 6 9 x 2 + -3.67490842 x^3 + 41.06730769 x^2 + − 3 . 6 7 4 9 0 8 4 2 x 3 + 4 1 . 0 6 7 3 0 7 6 9 x 2 + − 1 4 9 . 9 2 0 8 6 0 8 1 x + 1 8 4 . 7 5 6 9 2 3 0 8 − 6 . 0 = 0 -149.92086081 x + 184.75692308 - 6.0 = 0 − 1 4 9 . 9 2 0 8 6 0 8 1 x + 1 8 4 . 7 5 6 9 2 3 0 8 − 6 . 0 = 0
La ejecución del algoritmo de búsqueda queda como tarea .
Algoritmo en python para obtener la gráfica y respuesta a la matriz:
# Método de Gauss-Jordan ,
# Recibe las matrices A,B
# presenta solucion X que cumple: A.X=B
import numpy as np
import matplotlib.pyplot as plt
# INGRESO
puntos = np.array([[3.2, 5.12],
[3.8, 6.42],
[4.2, 7.25],
[4.5, 6.85]])
A = np.array([[4.5**3 , 4.5**2 , 4.5 , 1],
[4.2**3 , 4.2**2 , 4.2 , 1],
[3.8**3 , 3.8**2 , 3.8 , 1],
[3.2**3 , 3.2**2 , 3.2, 1]])
B = np.array([[6.85],
[7.25],
[6.42],
[5.12]])
# PROCEDIMIENTO
casicero = 1e-15 # 0
AB = np.concatenate((A,B),axis=1)
tamano = np.shape(AB)
n = tamano[0]
m = tamano[1]
print ('matriz aumentada: ' )
print (AB)
# Gauss elimina hacia adelante
# tarea: verificar términos cero
for i in range (0,n,1):
pivote = AB[i,i]
adelante = i+1
for k in range (adelante,n,1):
if (np.abs(pivote)>=casicero):
factor = AB[k,i]/pivote
AB[k,:] = AB[k,:] - factor*AB[i,:]
print ('Elimina hacia adelante' )
print (AB)
# Gauss-Jordan elimina hacia atras
ultfila = n-1
ultcolumna = m-1
for i in range (ultfila,0-1,-1):
# Normaliza a 1 elemento diagonal
AB[i,:] = AB[i,:]/AB[i,i]
pivote = AB[i,i] # uno
# arriba de la fila i
atras = i-1
for k in range (atras,0-1,-1):
if (np.abs(AB[k,i])>=casicero):
factor = pivote/AB[k,i]
AB[k,:] = AB[k,:]*factor - AB[i,:]
else :
factor= 'division para cero'
print ('Elimina hacia atras' )
print (AB)
X = AB[:,ultcolumna]
# Verifica resultado
verifica = np.dot(A,X)
# SALIDA
print ('el vector solución X es:' )
print (np.transpose([X]))
print ('verificar que A.X = B' )
print (np.transpose([verifica]))
# Revisa polinomio
a = np.min(puntos[:,0])
b = np.max(puntos[:,0])
muestras = 51
px = lambda x: X[0]*x**3 + X[1]*x**2 +X[2]*x + X[3]
xi = np.linspace(a,b,muestras)
pxi = px(xi)
# gráfica
plt.plot(xi,pxi)
plt.plot(puntos[:,0],puntos[:,1],'ro' )
plt.show()