Ejercicio: 1Eva_IIT2011_T2 Sistema de Ecuaciones, diagonal dominante
1. Desarrollo analítico
Solución iterativa usando el método de Jacobi
El sistema de ecuaciones
\begin{cases} -2x+5y+9z=1\\7x+y+z=6\\-3x+7y-z=-26\end{cases}cambia a su forma matricial AX=B
\begin{bmatrix} -2 & 5 & 9 \\ 7 & 1 & 1 \\ -3 & 7 &-1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} 1 \\ 6 \\ -26 \end{bmatrix}y luego como matriz aumentada y realizar el pivoteo parcial por filas, buscando hacerla diagonal dominante:
\begin{pmatrix} 7 & 1 & 1 &6\\ -3 & 7 &-1 & -26\\ -2 & 5 & 9 &1 \end{pmatrix}las ecuaciones para el algoritmo se obtienen despejando una variable diferente en cada ecuación.
x_{i+1}=\frac{6-y_i-z_i}{7} y_{i+1}=\frac{-26+3x_i+z_i}{7} z_{i+1}=\frac{1+2x_i-5y_i}{9}Dado el vector inicial X0= [0, 0, 0], y una tolerancia de 0.0001, e desarrollan al menos 3 iteraciones:
El error se verifica para éste ejercicio como el mayor valor de la diferencia entre iteraciones consecutivas. Analogía al video del acople entre las aeronaves. Si una coordenada aún no es la correcta …. menor a lo tolerado, pues NO hay acople…
itera = 0
x_1=\frac{6-(0)-(0)}{7} = 0.8571 y_1=\frac{-26+3(0)+(0)}{7} = -3,7142 z_1=\frac{1+2(0)-5(0)}{9} =0.111 diferencia = [ 0.8571 -0 , -3,7142 -0 ,0.1111- 0 ] = [ 0.8571 , -3,7142,0.1111 ] errado = max |diferencia| = 3,7142error es más alto que lo tolerado
X_1= [ 0.8571 , -3.7142 ,0.1111 ]Itera = 1
x_2=\frac{6-(-3,7142) -0.1111}{7} = 1.3718 y_2=\frac{-26+3(0.8571)+0.1111}{7} = -3.3310 z_2=\frac{1+2(0.8571)-5(-3,7142)}{9} = 2.3650 diferencia = [ 1.3718-0.8571 , -3.3310 -(-3.7142) , 2.3650 - 0.1111 ] = [0.5146 , 0.3832, 2.2539 ] errado = max |diferencia| = 2.2539el error disminuye, pero es más alto que lo tolerado
X_2= [ 1.3718 , -3.3310, 2.3650 ]Itera = 2
x_3 = \frac{6-(-3.3310)-2.3650}{7} = 0.9951 y_3 = \frac{-26+3(1.3718)+2.3650}{7} = -2.7884 z_3 = \frac{1+2(1.3718)-5(-3.3310)}{9} = 2.2665 diferencia = [ 0.9951 - 1.3718 , -2.7884 -(-3.3310) , 2.2665- 2.3650] diferencia = [ -0.3766 , 0.5425 , -0.0985] errado = max |diferencia| = 0.5425el error disminuye, pero es más alto que lo tolerado
X_3= [ 0.9951 , -2.7884 , 2.2665]Observación: Si el error disminuye en cada iteración, se puede intuir que se converge a la solución. Se puede continuar con la 4ta iteración…
2. Solución numérica usando Python
Usando el algoritmo desarrollado en clase se obtiene la respuesta con 13 iteraciones:
Matriz aumentada [[ -2. 5. 9. 1.] [ 7. 1. 1. 6.] [ -3. 7. -1. -26.]] Pivoteo parcial: 1 intercambiar filas: 0 y 1 2 intercambiar filas: 1 y 2 AB Iteraciones Jacobi itera,[X],errado 0 [0. 0. 0.] 1.0 1 [ 0.85714286 -3.71428571 0.11111111] 3.7142857142857144 2 [ 1.37188209 -3.33106576 2.36507937] 2.2539682539682544 3 [ 0.99514091 -2.78846777 2.26656589] 0.5425979915775843 4 [ 0.93170027 -2.96400162 1.8814023 ] 0.3851635892452223 5 [ 1.0117999 -3.04621384 1.96482318] 0.0834208883015708 6 [ 1.01162724 -2.99996816 2.02829656] 0.06347337312830126 7 [ 0.99595309 -2.99097453 2.00256614] 0.025730417621558477 8 [ 0.99834406 -3.0013678 1.99408654] 0.010393267289710018 9 [ 1.00104018 -3.00155447 2.0003919 ] 0.006305364149447268 10 [ 1.00016608 -2.99949822 2.00109475] 0.002056248145824391 11 [ 0.99977193 -2.99977243 1.99975814] 0.0013366043333828959 12 [ 1.00000204 -3.0001323 1.99982289] 0.0003598675094789172 13 [ 1.0000442 -3.00002443 2.00007395] 0.0002510632800638568 14 [ 0.99999292 -2.99997049 2.00002339] 5.3934767063168465e-05 respuesta de A.X=B : [ 0.99999292 -2.99997049 2.00002339] iterado, incluyendo X0: 15
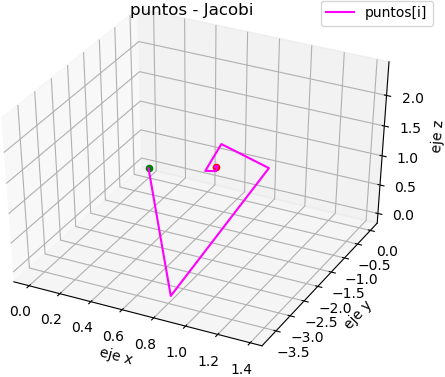
La gráfica muestra las coordenadas de las aproximaciones, observe el espiral que se va cerrando desde el punto inicial en verde al punto final en rojo.
Se debe controlar el número de iteraciones para verificar la convergencia con iteramax.
NO es necesario almacenar los valores de los puntos, solo el último valor y el contador itera permite determinar si el sistema converge.
# 1Eva_IIT2011_T2 Sistema de Ecuaciones, diagonal dominante # MATG1052 Métodos Numéricos # propuesta: edelros@espol.edu.ec, import numpy as np def jacobi(A,B,X0, tolera, iteramax=100, vertabla=False): ''' Método de Jacobi, tolerancia, vector inicial X0 para mostrar iteraciones: vertabla=True ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) X0 = np.array(X0,dtype=float) tamano = np.shape(A) n = tamano[0] m = tamano[1] diferencia = np.ones(n, dtype=float) errado = np.max(diferencia) X = np.copy(X0) xnuevo = np.copy(X0) tabla = [np.copy(X0)] itera = 0 if vertabla==True: print('Iteraciones Jacobi') print('itera,[X],errado') print(itera, xnuevo, errado) while not(errado<=tolera or itera>iteramax): for i in range(0,n,1): nuevo = B[i] for j in range(0,m,1): if (i!=j): # excepto diagonal de A nuevo = nuevo-A[i,j]*X[j] nuevo = nuevo/A[i,i] xnuevo[i] = nuevo diferencia = np.abs(xnuevo-X) errado = np.max(diferencia) X = np.copy(xnuevo) tabla = np.concatenate((tabla,[X]),axis = 0) itera = itera + 1 if vertabla==True: print(itera, xnuevo, errado) # No converge if (itera>iteramax): X=itera print('iteramax superado, No converge') return(X,tabla) def pivoteafila(A,B,vertabla=False): ''' Pivotea parcial por filas, entrega matriz aumentada AB Si hay ceros en diagonal es matriz singular, Tarea: Revisar si diagonal tiene ceros ''' A = np.array(A,dtype=float) B = np.array(B,dtype=float) # Matriz aumentada nB = len(np.shape(B)) if nB == 1: B = np.transpose([B]) AB = np.concatenate((A,B),axis=1) if vertabla==True: print('Matriz aumentada') print(AB) print('Pivoteo parcial:') # Pivoteo por filas AB tamano = np.shape(AB) n = tamano[0] m = tamano[1] # Para cada fila en AB pivoteado = 0 for i in range(0,n-1,1): # columna desde diagonal i en adelante columna = np.abs(AB[i:,i]) dondemax = np.argmax(columna) # dondemax no es en diagonal if (dondemax != 0): # intercambia filas temporal = np.copy(AB[i,:]) AB[i,:] = AB[dondemax+i,:] AB[dondemax+i,:] = temporal pivoteado = pivoteado + 1 if vertabla==True: print(' ',pivoteado, 'intercambiar filas: ',i,'y', dondemax+i) if vertabla==True: if pivoteado==0: print(' Pivoteo por filas NO requerido') else: print('AB') return(AB) # PROGRAMA Búsqueda de solucion # INGRESO -------- # INGRESO A = [[-2, 5, 9], [ 7, 1, 1], [-3, 7,-1]] B = [1, 6,-26] X0 = [0, 0, 0] tolera = 0.0001 iteramax = 100 # PROCEDIMIENTO -------- AB = pivoteafila(A,B,vertabla=True) # separa matriz aumentada en A y B [n,m] = np.shape(AB) A = AB[:,:m-1] B = AB[:,m-1] [X, puntos] = jacobi(A,B,X0,tolera,vertabla=True) iterado = len(puntos) # SALIDA -------- print('respuesta de A.X=B : ') print(X) print('iterado, incluyendo X0: ', iterado) # GRAFICA DE ITERACIONES import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D figura = plt.figure() # Una hoja para dibujar grafica = figura.add_subplot(111,projection = '3d') # Puntos de la iteración pxi = puntos[:,0] pyi = puntos[:,1] pzi = puntos[:,2] grafica.plot(pxi,pyi,pzi, color = 'magenta', label = 'puntos[i]') grafica.scatter(pxi[0],pyi[0],pzi[0], color = 'green', marker='o') grafica.scatter(pxi[iterado-1],pyi[iterado-1],pzi[iterado-1], color = 'red', marker='o') grafica.set_title('Puntos de iteración') grafica.set_xlabel('eje x') grafica.set_ylabel('eje y') grafica.set_zlabel('eje z') grafica.legend() plt.show()
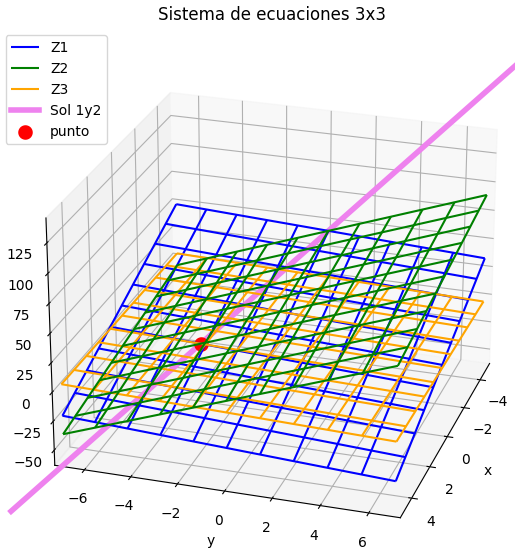
Gráfica de planos
Dado que el sistema de ecuaciones es de tres incógnitas, la solución se puede interpretar como la intersección de los planos formados por cada una de las ecuaciones en el espacio X,Y,Z.
se comenta la última instrucción del algoritmo anterior, #plt.show(), y se añaden las siguientes líneas al algoritmo anterior para obtener la gráfica:
# Tema 2. Sistema de ecuaciones 3x3 # Concepto como interseccion de Planos ##import matplotlib.pyplot as plt ##from mpl_toolkits.mplot3d import Axes3D ax = -5 # Intervalo X bx = 5 ay = ax-2 # Intervalo Y by = bx+2 muestras = 11 # PROCEDIMIENTO -------- # Ecuaciones de planos z0 = lambda x,y: (-A[0,0]*x - A[0,1]*y + B[0])/A[0,2] z1 = lambda x,y: (-A[1,0]*x - A[1,1]*y + B[1])/A[1,2] z2 = lambda x,y: (-A[2,0]*x - A[2,1]*y + B[2])/A[2,2] xi = np.linspace(ax,bx, muestras) yi = np.linspace(ay,by, muestras) Xi, Yi = np.meshgrid(xi,yi) Z0 = z0(Xi,Yi) Z1 = z1(Xi,Yi) Z2 = z2(Xi,Yi) # solución al sistema punto = np.linalg.solve(A,B) # SALIDA print('respuesta de A.X=B : ') print(punto) # Interseccion entre ecuación 1 y 2 # PlanoXZ, extremo inferior de y Aa = np.copy(A[0:2,[0,2]]) Ba = np.copy(B[0:2]) Ba = Ba-ay*A[0:2,1] pta = np.linalg.solve(Aa,Ba) pa = np.array([ay]) pxza = np.array([pta[0],ay,pta[1]]) # PlanoXZ, extremo superior de y Bb = np.copy(B[0:2]) Bb = Bb-by*A[0:2,1] ptb = np.linalg.solve(Aa,Bb) pb = np.array([by]) pxzb = np.array([ptb[0],by,ptb[1]]) # GRAFICA de planos fig3D = plt.figure() graf3D = fig3D.add_subplot(111, projection='3d') graf3D.plot_wireframe(Xi,Yi,Z0, color ='blue', label='Z1') graf3D.plot_wireframe(Xi,Yi,Z1, color ='green', label='Z2') graf3D.plot_wireframe(Xi,Yi,Z2, color ='orange', label='Z3') # recta intersección planos 1 y 2 graf3D.plot([pxza[0],pxzb[0]], [pxza[1],pxzb[1]], [pxza[2],pxzb[2]], label='Sol 1y2', color = 'violet', linewidth = 4) # Punto solución del sistema 3x3 graf3D.scatter(punto[0],punto[1],punto[2], color = 'red', marker='o', label ='punto', linewidth = 6) graf3D.set_title('Sistema de ecuaciones 3x3') graf3D.set_xlabel('x') graf3D.set_ylabel('y') graf3D.set_zlabel('z') graf3D.set_xlim(ax, bx) graf3D.set_xlim(ay, by) graf3D.legend() graf3D.view_init(45, 45) # rotacion de ejes for angulo in range(45, 360+45, 5 ): graf3D.view_init(45, angulo) plt.draw() plt.pause(.001) plt.show()
Tarea: Realice las modificaciones necesarias para usar el algoritmo de Gauss-Seidel. Luego compare resultados.
Revisión de resultados
Si se usan las ecuaciones sin pivorear y cambiar a diagonal dominante, como fueron presentadas en el enunciado, el algoritmo Jacobi NO converge, el error aumenta, y muy rápido como para observar la espiral hacia afuera en una gráfica.
Xi, errado [ -0.5 6. 26. ] 26.0 [ 131.5 -16.5 69.5] 132.0 [ 271. -984. -484.] 967.5 [-4638.5 -1407. -7675. ] 7191.0 [-38055.5 40150.5 4092.5] 41557.5 [ 118792. 262302. 395246.] 391153.5 [ 2434361.5 -1226784. 1479764. ] 2315569.5 [ 3591977.5 -18520288.5 -15890546.5] 17370310.5 ....