s1Eva_IIT2018_T1 Interpolar velocidad del paracaidista

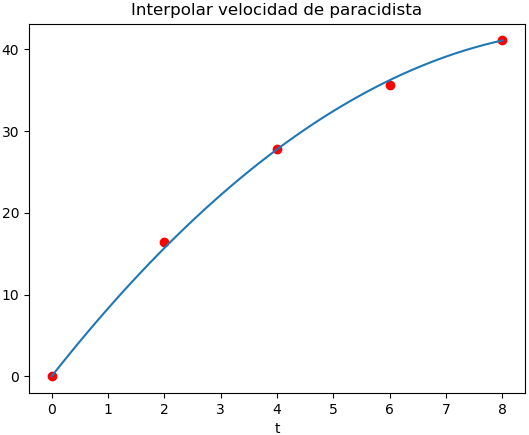
Ejercicio: 1Eva_IIT2018_T1 Interpolar velocidad del paracaidista

El ejercicio tiene dos partes: la interpolación y el integral.

Literal a

t	[s]	0	2	4	6	8
v(t)	[m/s]	0.0	16.40	27.77	35.64	41.10

No se especifica el método a seguir, por lo que se puede seleccionar el de mayor preferencia.

Por ejemplo. usando el método de Lagrange, con los puntos primero, medio y último, para cubrir todo el intervalo:

p_2(t) = 0\frac{(t-4)(t-8)}{(0-4)(0-8)} + + 27.77\frac{(t-0)(t-8)}{(4-0)(4-8)} + + 41.10\frac{(t-0)(t-4)}{(8-0)(8-4)} p_2(t) = 0 + 27.77\frac{t(t-8)}{-16}) + + 41.10\frac{t(t-4)}{32} p_2(t) = -1.73(t^2-8t) + 1.28(t^2-4t) p_2(t) = -0.45 t^2 + 8.74t

---

Literal b

El tema de integración para primera evaluación se realiza de forma analítica.

Una de las formas, que es independiente si se resolvió el literal a, es usar los datos proporcionados en la tabla el ejercicio:

t	[s]	0	2	4	6	8
v(t)	[m/s]	0.0	16.40	27.77	35.64	41.10

Se podría usar el método de Simpson de 1/3, puesto que los tamaños de paso en t son equidistantes se puede aplicar: h=2-0=2

\int_0^8 v(t)dt = \frac{2}{3}\Big( 0+ 4(16.40)+27.77\Big) + \frac{2}{3}\Big( 27.77+ 4(35.64)+41.10\Big) =203.2

con error del orden de O(h⁵) que al considerar h=2 no permite hacer una buena estimación del error. Sin embargo la respuesta es bastante cercana si se usa el método el trapecio con el algoritmo:

    valores de fi:  [ 0.   27.77 41.1 ]
divisores en L(i):  [ 32. -16.  32.]

Polinomio de Lagrange, expresiones
-1.735625*x*(x - 8.0) + 1.284375*x*(x - 4.0)

Polinomio de Lagrange: 
-0.45125*x**2 + 8.7475*x
Método del trapecio
distancia recorrida:  193.28
>>> 

El error entre los métodos es |203.2-193.28|= 9.92

Revisar el resultado usando un método con mayor precisión que el trapecio.

---

Algoritmo con Python

Las instrucciones en Python para el ejercicio son:

# 1ra Evaluación II Término 2018
# Tema 1. Interpolar velocidad del paracaidista
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# Literal a)
# Interpolacion de Lagrange
# divisoresL solo para mostrar valores

# INGRESO
t = [0.0, 2, 4, 6, 8]
v = [0.0, 16.40, 27.77, 35.64, 41.10]

cuales = [0,2,4]

# PROCEDIMIENTO
xi = np.array(t,dtype=float)
fi = np.array(v,dtype=float)

xi = xi[cuales]
fi = fi[cuales]

# Polinomio de Lagrange
n = len(xi)
x = sym.Symbol('x')
polinomio = 0
divisorL = np.zeros(n, dtype = float)
for i in range(0,n,1):
    
    # Termino de Lagrange
    numerador = 1
    denominador = 1
    for j  in range(0,n,1):
        if (j!=i):
            numerador = numerador*(x-xi[j])
            denominador = denominador*(xi[i]-xi[j])
    terminoLi = numerador/denominador

    polinomio = polinomio + terminoLi*fi[i]
    divisorL[i] = denominador

# simplifica el polinomio
polisimple = polinomio.expand()

# para evaluación numérica
px = sym.lambdify(x,polisimple)

# Puntos para la gráfica
muestras = 51
a = np.min(xi)
b = np.max(xi)
pxi = np.linspace(a,b,muestras)
pfi = px(pxi)

# SALIDA
print('    valores de fi: ',fi)
print('divisores en L(i): ',divisorL)
print()
print('Polinomio de Lagrange, expresiones')
print(polinomio)
print()
print('Polinomio de Lagrange: ')
print(polisimple)

# Gráfica
plt.plot(t,v,'o', label = 'Puntos')
plt.plot(xi,fi,'o', label = 'Puntos en polinomio')
plt.plot(pxi,pfi, label = 'Polinomio')
plt.legend()
plt.xlabel('xi')
plt.ylabel('fi')
plt.title('Interpolación Lagrange')
plt.grid()
plt.show()

# Literal b
# INGRESO
# El ingreso es el polinomio en forma lambda
# se mantienen las muestras

# intervalo de integración
# a, b seleccionados para la gráfica anterior
tramos = muestras -1

# PROCEDIMIENTO
def integratrapecio_fi(xi,fi):
    ''' sobre muestras de fi para cada xi
        integral con método de trapecio
    '''
    n = len(xi)
    suma = 0
    for i in range(0,n-1,1):
        dx = xi[i+1]-xi[i]
        untrapecio = dx*(fi[i+1]+fi[i])/2
        suma = suma + untrapecio
    return(suma)


tramos = muestras-1
# PROCEDIMIENTO
distancia = integratrapecio_fi(xi,fi)

# SALIDA
print('Método del trapecio')
print('distancia recorrida: ', distancia)