s1Eva_IIT2018_T3 Interpolar con sistema de ecuaciones

Ejercicio: 1Eva_IIT2018_T3 Interpolar con sistema de ecuaciones

Los datos del ejercicio proporcionados son:

i	0	1	2	3	4	5
x	1.0	1.1	1.3	1.5	1.9	2.1
y(x)	1.84	1.90	2.10	2.28	2.91	3.28

Literal a

El tema es semejante al tema 1, cambiando el método de interpolación.
Se usan los puntos de las posiciones 0, 3 y 5.

p_2(x) = b_0 + b_1x + b_2 x^2

en la fórmula:

punto x[0] = 1, y[0]= 1.84

1.84 = b_0 + b_1(1) + b_2 (1)^2

1.84 = b_0 + b_1 + b_2

punto x[3] = 1.5, y[3]= 2.28

2.28 = b_0 + b_1(1.5) + b_2 (1.5)^2

2.28 = b_0 + 1.5 b_1 + 2.25 b_2

punto x[5] = 2.1, y[5]= 3.28

3.28= b_0 + b_1(2.1) + b_2 (2.1)^2

3.28= b_0 + 2.1 b_1 + 4.41 b_2

se obtiene el sistema de ecuaciones:

b_0 + b_1 + b_2 = 1.84

b_0 + 1.5 b_1 + 2.25 b_2 = 2.28

b_0 + 2.1 b_1 + 4.41 b_2 = 3.28

Con lo que se plantea la forma Ax=B:

A = \begin{bmatrix} 1 & 1 & 1\\ 1 & 1.5 & 2.25 \\1 & 2.1 & 4.41 \end{bmatrix}

B = \begin{bmatrix} 1.84\\ 2.28 \\ 3.28 \end{bmatrix}

Matriz Aumentada

AB = \begin{bmatrix} 1 & 1 & 1 & 1.84 \\ 1 & 1.5 & 2.25 & 2.28 \\1 & 2.1 & 4.41 &3.28 \end{bmatrix}

Pivoteo parcial por filas

Para el primer pivote no se requieren cambio de filas.
para el segundo pivote de la diagonal se deben intercambiar la fila segunda con la tercera

\begin{bmatrix} 1 & 1 & 1 & 1.84 \\ 1 & 2.1 & 4.41 &3.28 \\ 1 & 1.5 & 2.25 & 2.28 \end{bmatrix}

Se aplica eliminación hacia adelante:

fila = 0, columna=0 pivote = AB[0,0]=1

factor entre las filas es 1/1=1.

\begin{bmatrix}1 & 1 & 1 & 1.84 \\ 1-1 & 2.1-1 & 4.41 -1 &3.28 -1.84 \\ 1-1 & 1.5 -1 & 2.25 -1 & 2.28 - 1.84 \end{bmatrix}

\begin{bmatrix} 1 & 1 & 1 & 1.84 \\ 0 & 1.1 & 3.41 &1.44 \\ 0 & 0.5 & 1.25 & 0.44 \end{bmatrix}

fila =1, columna=1, pivote=AB[1,1] =1.1

factor entre filas es 0.5/1.1 = 1/2.2

\begin{bmatrix} 1 & 1 & 1 & 1.84 \\ 0 & 1.1 & 3.41 &1.44 \\ 0 & 0.5 -\frac{0.5}{1.1}(1.1)& 1.25 -\frac{0.5}{1.1}(3.41)& 0.44-\frac{0.5}{1.1}(1.44) \end{bmatrix}

\begin{bmatrix} 1 & 1 & 1 & 1.84 \\ 0 & 1.1 & 3.41 &1.44 \\ 0 & 0 & -0.3 & -0.214545 \end{bmatrix}

aplicando sustitución hacia atrás

b2 = -0.21/(-0.3) = 0.71515

b1= \frac{1.44-3.41 b_2}{1.1} = \frac{1.44-3.41( 0.71515)}{1.1}=-0.9078

b3= \frac{1.84-b_1-b_2}{1} = \frac{1.84-(-0.9078)-(0.71515)}{1} =2.0327

con lo que el polinomio buscado es:

p_2(x) = 2.0327 -0.9078 x + 0.71515 x^2

y se obtiene el resultado de la interpolación.

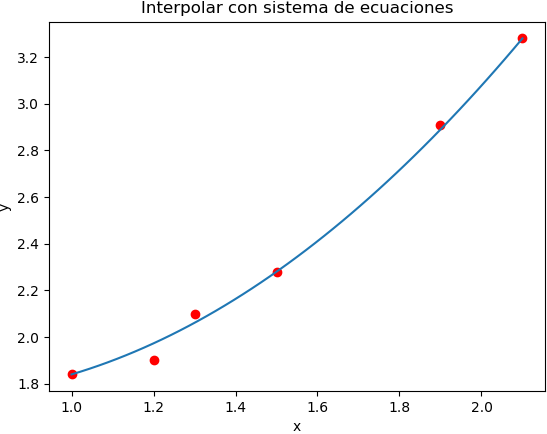Observación: En la gráfica se muestra que el polinomio pasa por los puntos seleccionados de la tabla. En los otros puntos hay un error que se puede calcular como la resta del punto y su valor con p(x). Queda como tarea.

Usando el algoritmo del polinomio de interpolación con la matriz de Vandermonde se obtiene:

Matriz Vandermonde: 
[[1.   1.   1.  ]
 [2.25 1.5  1.  ]
 [4.41 2.1  1.  ]]
los coeficientes del polinomio: 
[ 0.71515152 -0.90787879  2.03272727]
Polinomio de interpolación: 
0.715151515151516*x**2 - 0.907878787878792*x + 2.03272727272728

 formato pprint
                   2                                         
0.715151515151516*x  - 0.907878787878792*x + 2.03272727272728
suma de columnas:  [3.   4.75 7.51]
norma D:  7.51
numero de condicion:  97.03737354737122
solucion: 
[ 0.71515152 -0.90787879  2.03272727]
>>>

Literal b

Se requiere calcular una norma de suma de filas. es suficiente para demostrar el conocimiento del concepto el usar A.

Se adjunta el cálculo del número de condición y la solución al sistema de ecuaciones:

suma de columnas:  [3.   4.75 7.51]
norma A:  7.51
numero de condición:  97.03737354737129
solución: 
[ 2.03272727 -0.90787879  0.71515152]

El comentario importante corresponde al número de condición, que es un número muy alto para usar un método iterativo, por lo que la solución debe ser un método directo.
Se puede estimar será un número mucho mayor que 1, pues la matriz no es diagonal dominante.

Instrucciones en Python

# 1Eva_IIT2018_T3 Interpolar con sistema de ecuaciones
# El polinomio de interpolación
import numpy as np
import sympy as sym
import matplotlib.pyplot as plt

# INGRESO
xj = [1.0,  1.1,  1.3,  1.5,  1.9,  2.1 ]
yj = [1.84, 1.90, 2.10, 2.28, 2.91, 3.28]
cuales = [0, 3, 5]

# muestras = tramos+1
muestras = 51

# PROCEDIMIENTO
# Convierte a arreglos numpy 
xi = np.array(xj,dtype=float)
fi = np.array(yj,dtype=float)

xi = xi[cuales]
fi  = fi[cuales]
B = fi

n = len(xi)

# Matriz Vandermonde D
D = np.zeros(shape=(n,n),dtype =float)
for i in range(0,n,1):
    for j in range(0,n,1):
        potencia = (n-1)-j # Derecha a izquierda
        D[i,j] = xi[i]**potencia

# Aplicar métodos Unidad03. Tarea
# Resuelve sistema de ecuaciones A.X=B
coeficiente = np.linalg.solve(D,B)

# Polinomio en forma simbólica
x = sym.Symbol('x')
polinomio = 0
for i in range(0,n,1):
    potencia = (n-1)-i   # Derecha a izquierda
    termino = coeficiente[i]*(x**potencia)
    polinomio = polinomio + termino

# Polinomio a forma Lambda
# para evaluación con vectores de datos xin
px = sym.lambdify(x,polinomio)

# Para graficar el polinomio en [a,b]
a = np.min(xi)
b = np.max(xi)
xin = np.linspace(a,b,muestras)
yin = px(xin)

# Usando evaluación simbólica
##yin = np.zeros(muestras,dtype=float)
##for j in range(0,muestras,1):
##    yin[j] = polinomio.subs(x,xin[j])
    
# SALIDA
print('Matriz Vandermonde: ')
print(D)
print('los coeficientes del polinomio: ')
print(coeficiente)
print('Polinomio de interpolación: ')
print(polinomio)
print('\n formato pprint')
sym.pprint(polinomio)

# Grafica
plt.plot(xj,yj,'o', label='Puntos')
plt.plot(xi,B,'o', label='[xi,fi]')
plt.plot(xin,yin, label='p(x)')
plt.xlabel('xi')
plt.ylabel('fi')
plt.legend()
plt.title(polinomio)
plt.show()


# literal b
sumacolumnas = np.sum(D, axis =1)
norma = np.max(sumacolumnas)
print('suma de columnas: ', sumacolumnas)
print('norma D: ', norma)

numerocondicion = np.linalg.cond(D)
print('numero de condicion: ', numerocondicion)

solucion = np.linalg.solve(D,B)
print('solucion: ')
print(solucion)