s1Eva_IIT2019_T4 Concentración de químico

Ejercicio: 1Eva_IIT2019_T4 Concentración de químico

formula a usar:

$C = C_{ent} ( 1 - e^{-0.04t})+C_{0} e^{-0.03t}$

Se sustituyen los valores dados con:
C₀ = 4, C_ent = 10, C = 0.93 C_ent.

$0.93(10) = 10 ( 1 - e^{-0.04t}) + 4 e^{-0.03t}$

igualando a cero para forma estandarizada del algoritmo,

$10( 1 - e^{-0.04t}) + 4 e^{-0.03t} - 9.3 = 0$ $0.7 - 10 e^{-0.04t} + 4 e^{-0.03t} = 0$

se usas las funciones f(t) y f'(t) para el método de Newton-Raphson,

$f(t) = 0.7 - 10 e^{-0.04t} + 4 e^{-0.03t}$ $f'(t) = - 10(-0.04) e^{-0.04t} + 4(-0.03) e^{-0.03t}$ $f'(t) = 0.4 e^{-0.04t} - 0.12 e^{-0.03t}$

con lo que se pueden realizar los cálculos de forma iterativa.

$t_{i+1} = t_i -\frac{f(t_i)}{f'(t_i)}$

De no disponer de la gráfica de f(t), y se desconoce el valor inicial para t₀ se usa 0. Como no se indica la tolerancia, se estima en 10^-4

Iteración 1

t₀ = 0

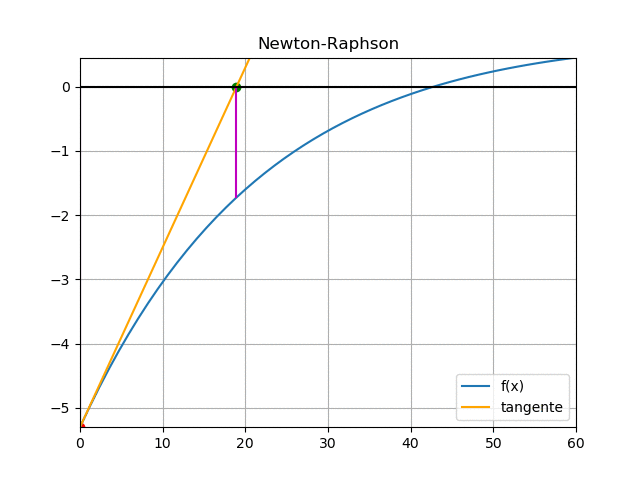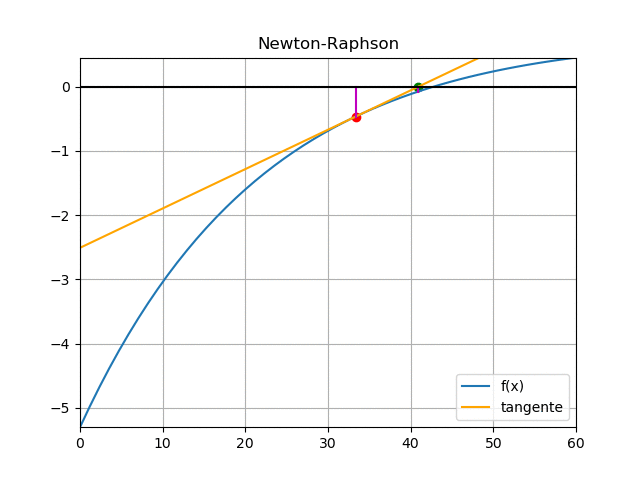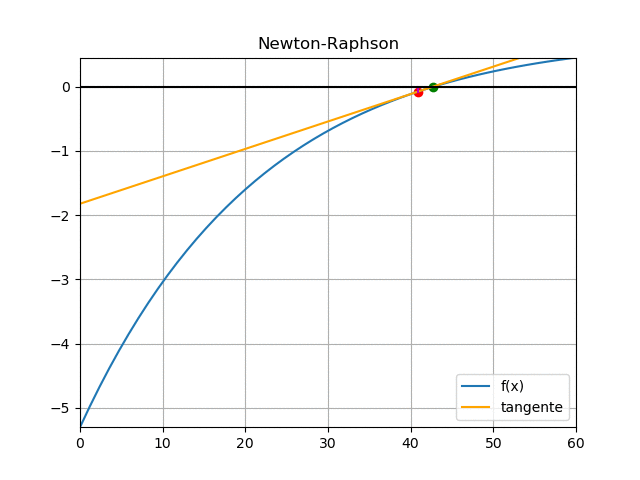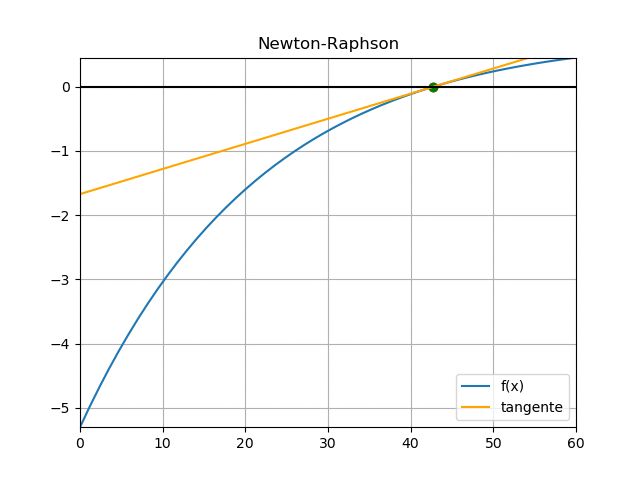
$f(0) = 0.7 - 10 e^{-0.04(0)} + 4 e^{-0.03(0)} = 5.3$ $f'(0) = 0.4 e^{-0.04(0)} - 0.12 e^{-0.03(0)} = -0.28$ $t_{1} = 0 -\frac{5.3}{-0.28} = 18.92$ $error = |18.92-0| = 18.92$

Iteración 2

$f(18.92) = 0.7 - 10 e^{-0.04(18.92)} + 4 e^{-0.03(18.92)} = -1.72308$ $f'(18.92) = 0.4 e^{-0.04(18.92)} - 0.12 e^{-0.03(18.92)} = 0.119593$ $t_{2} = 18.92 -\frac{-1.723087}{0.119593} = 33.3365$ $error = |33.3365 - 18.92| = 14.4079$

Iteración 3

$f(33.3365) = 0.7 - 10 e^{-0.04(33.3365)} + 4 e^{-0.03(33.3365)} = -0.4642$ $f'(33.3365) = 0.4 e^{-0.04(33.3365)} - 0.12 e^{-0.03(33.3365)} = 0.06128$ $t_{3} = 33.3365 -\frac{-0.46427}{-5.8013} = 40.912$ $error = |40.912 - 33.3365| = 7.5755$

Observando que los errores disminuyen entre cada iteración, se encuentra que el método converge.

y se forma la siguiente tabla:

['xi' ,  'xnuevo', 'error']
[ 0.      18.9286  18.9286]
[18.9286  33.3365  14.4079]
[33.3365  40.912    7.5755]
[40.912   42.654     1.742]
[42.654   42.7316   0.0776]
[4.2732e+01 4.2732e+01 1.4632e-04]
raiz en:  42.731721341402796

Observando la gráfica de la función puede observar el resultado:

---

Algoritmo en Python

# 1Eva_IIT2019_T4
# Método de Newton-Raphson

import numpy as np
import matplotlib.pyplot as plt

# INGRESO
fx = lambda t: 0.7-10*np.exp(-0.04*t)+4*np.exp(-0.03*t)
dfx = lambda t:0.40*np.exp(-0.04*t)-0.12*np.exp(-0.03*t)

x0 = 0
tolera = 0.001

a = 0
b = 60
muestras = 21

# PROCEDIMIENTO
tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

tabla = np.array(tabla)
n=len(tabla)

# para la gráfica
xk = np.linspace(a,b,muestras)
fk = fx(xk)

# SALIDA
print(['xi', 'xnuevo', 'error'])
np.set_printoptions(precision = 4)
for i in range(0,n,1):
    print(tabla[i])
print('raiz en: ', xi)

# grafica
plt.plot(xk,fk)
plt.axhline(0, color='black')
plt.xlabel('t')
plt.ylabel('f(t)')
plt.show()