Ejercicio: 1Eva_IT2009_T1 Demanda de un producto alcanza la producción
Desarrollo analítico
– igualar la ecuación al valor buscado, 80
200 t e^{-0.75t} = 80– forma estándar de la ecuación para el método f(x) = 0:
f(t) = 200 t e^{-0.75t} - 80– derivada de la ecuación
f'(t) = 200 e^{-0.75t} + 200 t (-0.75) e^{-0.75t} f'(t) = 200 e^{-0.75t}(1-0.75t)– fórmula del método de Newton-Raphson
t_{i+1} = t_i - \frac{f(t)}{f'(t)}– Punto inicial. Como la variable es t, tiempo, el rango de análisis es t>0
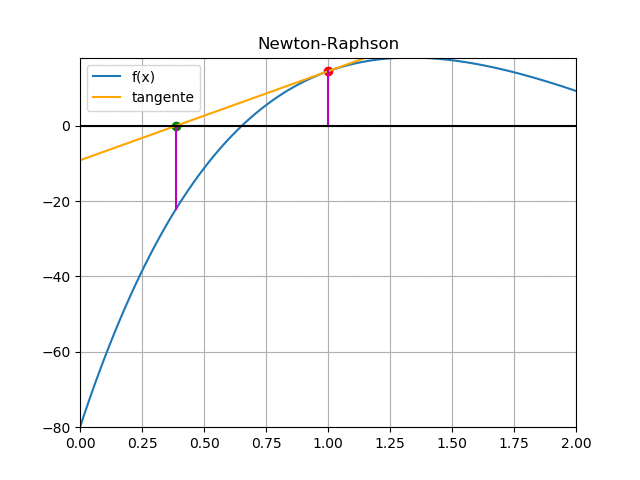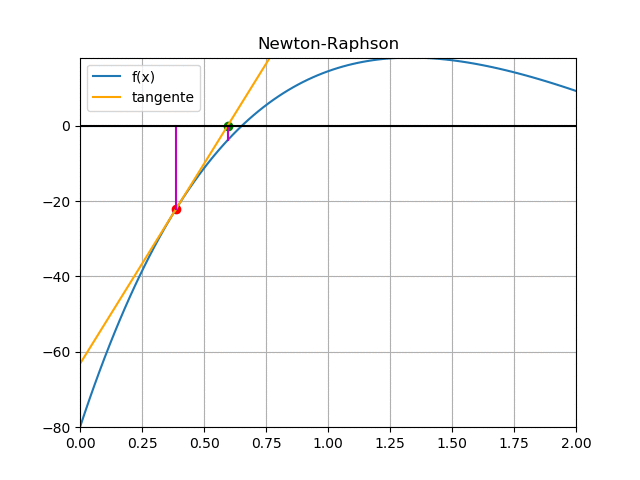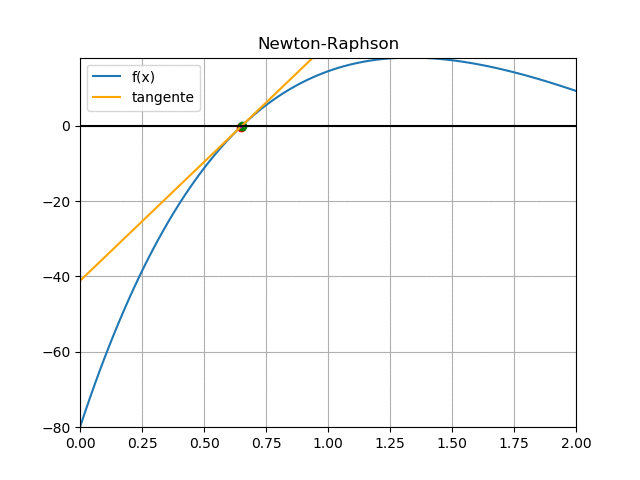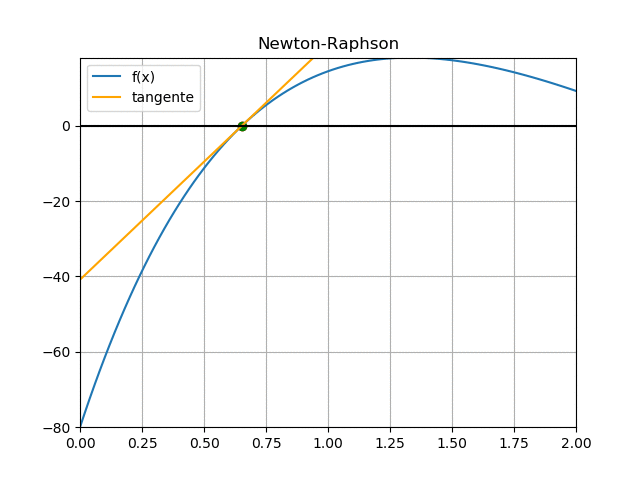
El valor inicial de búsqueda se selecciona t0 = 1
iteración 0:
f(1) = 200 (1) e^{-0.75(1)} - 80 =14.4733 f'(1) = 200 e^{-0.75(1)}(1-0.75(1)) = 23.6183 t_{1} = 1 - \frac{14.4733}{23.6183} =0.3872 error = |0.3872 - 1| = 0.6128iteración 1:
f(0.3872)= 200 (0.3872) e^{-0.75(0.3872)} - 80 = -22.0776 f'(0.3872 )= 200 e^{-0.75(0.3872)}(1-0.75(0.3872)) = 106.1511 t_{2} = 0.3872 - \frac{-22.0776}{106.1511} = 0.5952 error = |0.5952- 0.3872| = 0.208iteración 2:
f(0.5952)=200 (0.5952) e^{-0.75(0.5952)} - 80 = -3.8242 f'(0.5952) = 200 e^{-0.75(0.5952)}(1-0.75(0.5952)) = 70.855 t_{3} = 0.5952 - \frac{-3.8242}{70.855} = 0.64916 error = |0.64916-0.5952| = 0.053972
…
tabla de iteraciones
i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo'] 0 [ 1. 14.4733 23.6183 0.3872 0.6128] 1 [ 0.3872 -22.0776 106.1511 0.5952 0.208 ] 2 [ 5.9518e-01 -3.8242e+00 7.0855e+01 6.4916e-01 5.3972e-02] 3 [ 6.4916e-01 -2.1246e-01 6.3069e+01 6.5252e-01 3.3686e-03] 4 [ 6.5252e-01 -7.9031e-04 6.2600e+01 6.5254e-01 1.2625e-05] 5 [ 6.5254e-01 -1.1069e-08 6.2599e+01 6.5254e-01 1.7683e-10] raíz en: 0.6525363029069534
Se obtiene el valor de la raíz con 5 iteraciones, y un error de 1.2625e-05
Desarrollo con Python
# 1Eva_IT2009_T1 Demanda de un producto alcanza la producción import numpy as np import matplotlib.pyplot as plt def newton_raphson(fx,dfx,xi, tolera, iteramax=100, vertabla=False, precision=4): ''' fx y dfx en forma numérica lambda xi es el punto inicial de búsqueda ''' itera=0 tramo = abs(2*tolera) if vertabla==True: print('método de Newton-Raphson') print('i', ['xi','fi','dfi', 'xnuevo', 'tramo']) np.set_printoptions(precision) while (tramo>=tolera): fi = fx(xi) dfi = dfx(xi) xnuevo = xi - fi/dfi tramo = abs(xnuevo-xi) if vertabla==True: print(itera,np.array([xi,fi,dfi,xnuevo,tramo])) xi = xnuevo itera = itera + 1 if itera>=iteramax: xi = np.nan print('itera: ',itera, 'No converge,se alcanzó el máximo de iteraciones') return(xi) # INGRESO fx = lambda t: 200*t*np.exp(-0.75*t) - 80 dfx = lambda t: 200*np.exp(-0.75*t) + 200*t*(-0.75)*np.exp(-0.75*t) #fx = lambda t: 200*np.exp(-0.75*t) + 200*t*(-0.75)*np.exp(-0.75*t) #dfx = lambda t: (112.5*t - 300.0)*np.exp(-0.75*t) x0 = 1 tolera = 0.00001 # PROCEDIMIENTO respuesta = newton_raphson(fx,dfx,x0, tolera, vertabla=True) # SALIDA print('raíz en: ', respuesta)
Para la gráfica se añade:
# grafica
a = 0
b = 2
muestras = 21
xi = np.linspace(a,b,muestras)
fi = fx(xi)
plt.plot(xi,fi)
plt.axhline(0)
plt.xlabel('x')
plt.ylabel('f(x)')
plt.show()
Literal b
Para el caso de encontrar el máximo se usaría la expresión fb(t) cuando f'(t)= 0.
Con lo que para el algoritmo la expresión nueva f(t) es :
y fb‘(t) es f''(t):
se desarrolla las expresiones con Sympy :
>>> import sympy as sym
>>> t = sym.Symbol('t')
>>> f = 200*t*sym.exp(-0.75*t)-80
>>> sym.diff(f,t,1)
-150.0*t*exp(-0.75*t) + 200*exp(-0.75*t)
>>> sym.diff(f,t,2)
(112.5*t - 300.0)*exp(-0.75*t)
>>>
Se actualiza el algoritmo con las funciones:
fx = lambda t: 200*np.exp(-0.75*t) + 200*t*(-0.75)*np.exp(-0.75*t) dfx = lambda t: (112.5*t - 300.0)*np.exp(-0.75*t)
y se obtiene como resultado:
método de Newton-Raphson i ['xi', 'fi', 'dfi', 'xnuevo', 'tramo'] 0 [ 1. 23.6183 -88.5687 1.2667 0.2667] 1 [ 1.2667 3.8674 -60.9117 1.3302 0.0635] 2 [ 1.3302e+00 1.7560e-01 -5.5445e+01 1.3333e+00 3.1671e-03] 3 [ 1.3333e+00 4.1611e-04 -5.5183e+01 1.3333e+00 7.5406e-06] raíz en: 1.3333333332906878