Ejercicio: 1Eva_IT2011_T1_MN Fondo de inversión
Planteamiento
Siendo C(t), considerando A como un millón, A=1
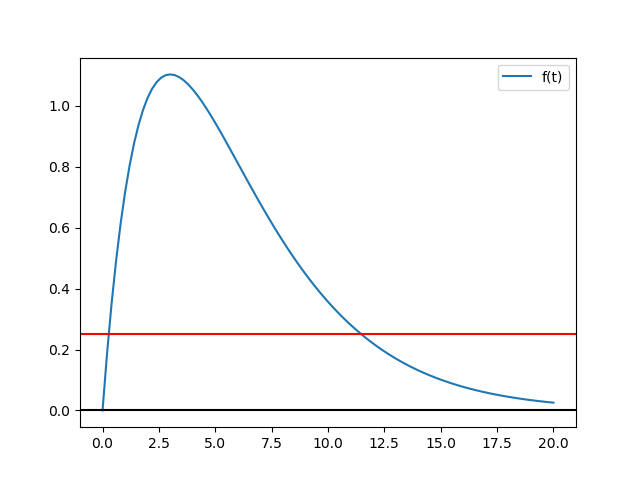
C(t)=Ate^{-t/3}Se observa la gráfica de la función que muestra el valor máximo en el intervalo entre [2, 5] , alrededor de 3
Para encontrar el valor del máximo, se requiere usar la derivada respecto al tiempo y encontrar el cruce por cero.
\frac{dC}{dt} = -t e^{-t/3} +e^{-t/3}Adicionalmente, para el literal b en la gráfica se incluye como meta donde C(t) disminuye a 1/4 o 0.25. Lo que estaría en el intervalo entre [10, 14].
Instrucciones en Python para observar la función:
# 1ra Evaluación I Término 2011 # Tema 1. Fondo de Inversion import numpy as np import matplotlib.pyplot as plt ft = lambda t: t*np.exp(-t/3) a=0 b=20 tolera = 0.0001 muestras = 101 meta = 0.25 # PROCEDIMIENTO # Observar la función entre [a,b] ti = np.linspace(a,b,muestras) fti = ft(ti) # Salida # Gráfica plt.plot(ti,fti, label='f(t)') plt.axhline(meta, color = 'r') plt.axhline(0, color = 'k') plt.legend() plt.show()
literal a
Para encontrar el máximo se puede determinar la derivada con Sympy.
Para la derivada se usa la forma simbólica de la función, que se convierte a forma numérica lambda para evaluarla de forma más fácil y obtener la gráfica.
# Literal a) usando derivada simbólica import sympy as sp x = sp.Symbol('x') fxs = x*sp.exp(-x/3) dfxs = fxs.diff(x,1) # convierte la expresión a lambda dfxn = sp.utilities.lambdify(x,dfxs,'numpy') dfxni = dfxn(ti) print('derivada de la función: ') print(dfxs) # Gráfica de la derivada. plt.plot(ti,dfxni, label='df(t)/dt') plt.axhline(0, color = 'k') plt.legend() plt.show()
derivada de la función: -x*exp(-x/3)/3 + exp(-x/3)
Se busca la raíz con algún método, por ejemplo bisección, siendo f(x) = 0
f(t) = \frac{dC}{dt} = -t e^{-t/3} +e^{-t/3}Desarrollo analítico
itera = 0, a = 2, b= 5
c = \frac{a+b}{2} =\frac{2+5}{2}=3.5 f(2) = -2 e^{-2/3} +e^{-2/3} =0.1711 f(3.5) = -5 e^{-3.5/3} +e^{-3.5/3} = -0.0519 f(5) = -5 e^{-5/3} +e^{-5/3} = -0.1259cambio de signo del lado izquierdo
a = 2, b = 3.5
error = | 3.5-2 | = 1.5
itera = 1, a = 2, b = 3.5
c = \frac{2+3.5}{2}=2.75 f(2.75) = -2.75 e^{-2.75/3} +e^{-2.75/3} = 0.0333cambio de signo del lado derecho
a = 2.75, b = 3.5
error = | 3.5-2.75 | = 0.75
itera = 2, a = 2.75, b = 3.5
c = \frac{2.75+3.5}{2}=3.125 f(3.125) = -3.125 e^{-3.125/3} +e^{-3.125/3} = -0.0147cambio de signo del lado izquierdo
a = 2.75, b = 3.1255
error = | 3.12555-2.75 | = 0.375
y se continúa hasta alcanzar la tolerancia dada para el ejercicio.
Usando el algoritmo se encuentra luego de 14 iteraciones:
método de Bisección i ['a', 'c', 'b'] ['f(a)', 'f(c)', 'f(b)'] tramo 0 [2. 3.5 5. ] [ 0.1711 -0.0519 -0.1259] 1.5 1 [2. 2.75 3.5 ] [ 0.1711 0.0333 -0.0519] 0.75 2 [2.75 3.125 3.5 ] [ 0.0333 -0.0147 -0.0519] 0.375 3 [2.75 2.9375 3.125 ] [ 0.0333 0.0078 -0.0147] 0.1875 4 [2.9375 3.0312 3.125 ] [ 0.0078 -0.0038 -0.0147] 0.09375 5 [2.9375 2.9844 3.0312] [ 0.0078 0.0019 -0.0038] 0.046875 6 [2.9844 3.0078 3.0312] [ 0.0019 -0.001 -0.0038] 0.0234375 7 [2.9844 2.9961 3.0078] [ 0.0019 0.0005 -0.001 ] 0.01171875 8 [2.9961 3.002 3.0078] [ 0.0005 -0.0002 -0.001 ] 0.005859375 9 [2.9961 2.999 3.002 ] [ 0.0005 0.0001 -0.0002] 0.0029296875 10 [2.999 3.0005 3.002 ] [ 1.1979e-04 -5.9866e-05 -2.3935e-04] 0.00146484375 11 [2.999 2.9998 3.0005] [ 1.1979e-04 2.9941e-05 -5.9866e-05] 0.000732421875 12 [2.9998 3.0001 3.0005] [ 2.9941e-05 -1.4968e-05 -5.9866e-05] 0.0003662109375 13 [2.9998 2.9999 3.0001] [ 2.9941e-05 7.4847e-06 -1.4968e-05] 0.00018310546875 14 [2.9999 3. 3.0001] [ 7.4847e-06 -3.7422e-06 -1.4968e-05] 9.1552734375e-05 raíz en: 3.000030517578125
Instrucciones en Python
# 1Eva_IT2011_T1_MN Fondo de Inversión # Algoritmo de Bisección # [a,b] se escogen de la gráfica de la función # error = tolera import numpy as np def biseccion(fx,a,b,tolera,iteramax = 20, vertabla=False, precision=4): ''' Algoritmo de Bisección Los valores de [a,b] son seleccionados desde la gráfica de la función error = tolera ''' fa = fx(a) fb = fx(b) tramo = np.abs(b-a) itera = 0 cambia = np.sign(fa)*np.sign(fb) if cambia<0: # existe cambio de signo f(a) vs f(b) if vertabla==True: print('método de Bisección') print('i', ['a','c','b'],[ 'f(a)', 'f(c)','f(b)']) print(' ','tramo') np.set_printoptions(precision) while (tramo>=tolera and itera<=iteramax): c = (a+b)/2 fc = fx(c) cambia = np.sign(fa)*np.sign(fc) if vertabla==True: print(itera,np.array([a,c,b]),np.array([fa,fc,fb])) if (cambia<0): b = c fb = fc else: a = c fa = fc tramo = np.abs(b-a) if vertabla==True: print(' ',tramo) itera = itera + 1 respuesta = c # Valida respuesta if (itera>=iteramax): respuesta = np.nan else: print(' No existe cambio de signo entre f(a) y f(b)') print(' f(a) =',fa,', f(b) =',fb) respuesta=np.nan return(respuesta) # INGRESO fx = lambda t: -t*np.exp(-t/3)/3 + np.exp(-t/3) a = 2 b = 5 tolera = 0.0001 # PROCEDIMIENTO respuesta = biseccion(fx,a,b,tolera,vertabla=True) # SALIDA print('raíz en: ', respuesta)
Determine el monto de la inversión inicial A necesaria para que el máximo sea igual a un millón de dólares. Como el máximo se encuentra en t=3, se tiene que:
C(t)=Ate^{-t/3} 1=A(3)e^{-3/3} A=\frac{1}{(3)e^{-1}} = 0.906093considerando que las unidades se encuentran en millones.
literal b
Para el literal b, se busca la raíz usando el método de Newton-Raphson como se indica en el enunciado.
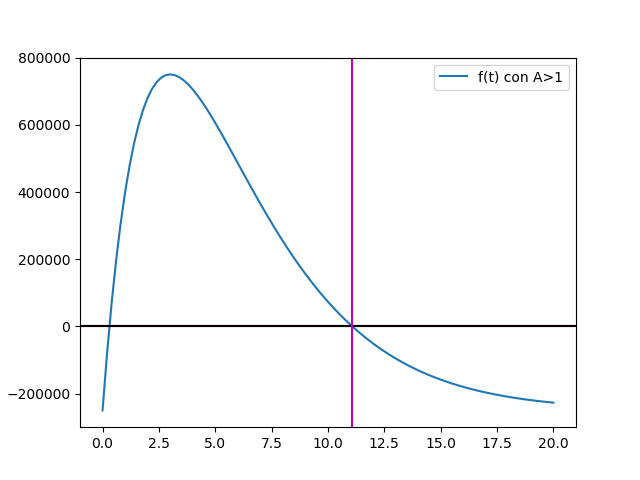
En la función nueva se usa el valor de A encontrado, y la meta establecida.
Se obtiene la misa derivada del problema anterior multiplicada por A, por ser solo un factor que multiplica a la función original. El valor de meta es una constante, que se convierte en cero al derivar.
resultado con el algoritmo:
['xi', 'xnuevo', 'tramo'] [[1.0000e+01 1.0880e+01 8.7987e-01] [1.0880e+01 1.1056e+01 1.7580e-01] [1.1056e+01 1.1076e+01 2.0098e-02] [1.1076e+01 1.1078e+01 1.9337e-03] [1.1078e+01 1.1078e+01 1.8202e-04]] raiz en: 11.077880437153812 con error de: 0.00018201925869298918 >>>
Instrucciones en Python
# 1Eva_IT2011_T1_MN Fondo de Inversión # Método de Newton-Raphson # Ejemplo 1 (Burden ejemplo 1 p.51/pdf.61) import numpy as np # INGRESO fx = lambda t: 0.906093*t*np.exp(-t/3) - 0.25 dfx = lambda t: -t*np.exp(-t/3)/3 + np.exp(-t/3) x0 = 10 tolera = 0.001 # PROCEDIMIENTO tabla = [] tramo = abs(2*tolera) xi = x0 while (tramo>=tolera): xnuevo = xi - fx(xi)/dfx(xi) tramo = abs(xnuevo-xi) tabla.append([xi,xnuevo,tramo]) xi = xnuevo # convierte la lista a un arreglo. tabla = np.array(tabla) n = len(tabla) # SALIDA print(['xi', 'xnuevo', 'tramo']) np.set_printoptions(precision = 4) print(tabla) print('raiz en: ', xi) print('con error de: ',tramo)
el valor de t para la meta es: 11.0779035867