Ejercicio: 1Eva_IT2015_T2 Salida cardiaca
Solución presentada como introducción al tema de interpolación y solución de sistemas de ecuaciones.
No realiza el literal c, no se desarrolla el tema de integrales.
Note que el desarrollo del tema permite aumentar el grado del polinomio de interpolación, lo que se afecta al tamaño del sistema de ecuaciones (matriz).
Los valores obtenidos con la solución propuesta son:
solución para X por Gauss-Seidel [[-0.42175867] [ 0.15610893] [ 0.02736763]] verifica que A.X = B: [[ -7.02831455e-05] [ 1.50012970e+00] [ 3.20000000e+00]] polinomio interpolación, con puntos: 3 0.0273676337623498*x**2 + 0.156108926206362*x - 0.421758670607596 >>>
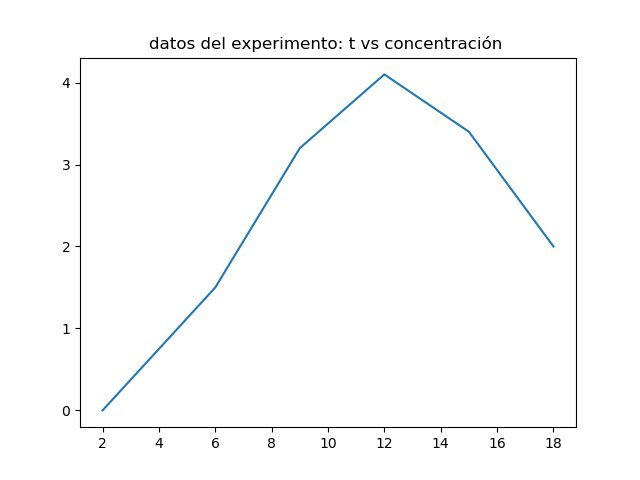
La gráfica para observar los datos experimentales es:
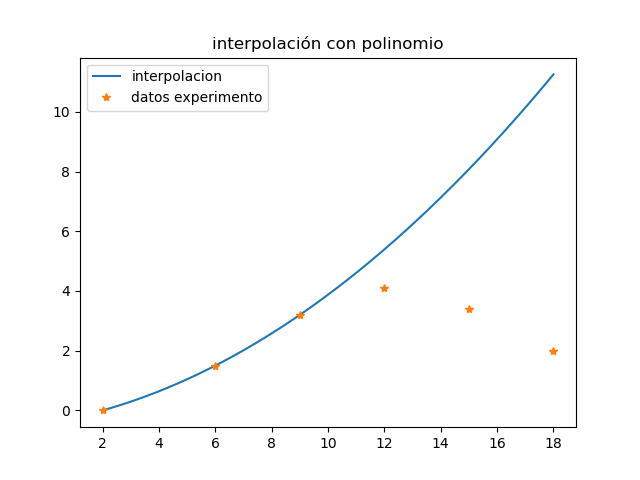
La gráfica con polinomio de interpolación de grado 2, con tres puntos:
instrucciones del problema para la solución por partes en python:
# 1ra Evaluación I Término 2015 # Tema 2. Flujo de sangre en corazón # Tarea: parte c), no se ha realizado el áre bajo curva # falta calcular salida cardiaca. import numpy as np import matplotlib.pyplot as plt # Gráfica de datos experimentales: t = np.array([2,6,9,12,15,18]) y = np.array([0,1.5,3.2,4.1,3.4,2.0]) # SALIDA plt.plot(t,y) plt.title('datos del experimento: t vs concentración ') plt.show() # Sistema de ecuaciones para aproximar a polinomio grado 2 # para grado dos usa tres puntos, # por ejemplo usando el punto [ 2, 0] del experimento # a + b*(2) + c*(2**2) = 0 A = np.array([[1,2,2**2], [1,6,6**2], [1,9,9**2]]) B = np.array([[0], [1.5], [3.2]]) tolera = 0.0001 X = np.zeros(len(B), dtype = float) # usando numpy para solucion de matrices # Xnp = np.linalg.solve(A,B) # print('solución para A.X=B con numpy') # print(Xnp) # algoritmo Gauss-Seidel iteramax=100 tamano = np.shape(A) n = tamano[0] m = tamano[1] diferencia = np.ones(n, dtype=float) errado = np.max(diferencia) itera = 0 while (errado>tolera or itera>iteramax): for i in range(0,n,1): nuevo = B[i] for j in range(0,m,1): if (i!=j): # excepto diagonal de A nuevo = nuevo-A[i,j]*X[j] nuevo = nuevo/A[i,i] diferencia[i] = np.abs(nuevo-X[i]) X[i] = nuevo errado = np.max(diferencia) itera = itera + 1 # Vector en columna X = np.transpose([X]) # No converge if (itera>iteramax): X=0 Xgs = X # Metodo numérico Gauss_Seidel verifica = np.dot(A,Xgs) print('solución para X por Gauss-Seidel') print(Xgs) # verificar resultado print('verifica que A.X = B: ') print(verifica) # Observar interpolacion con polinomio creado pt = lambda t: Xgs[0,0]+ Xgs[1,0]*t + Xgs[2,0]*t**2 ti = np.linspace(2,18,501) pti = pt(ti) plt.plot(ti,pti, label = 'interpolacion') plt.plot(t,y,'*', label = 'datos experimento') plt.title('interpolación con polinomio') plt.legend() plt.show() # polinomio en sympy import sympy as sp x = sp.Symbol('x') polinomio = 0 k = len(Xgs) for i in range(0,k,1): polinomio = polinomio + Xgs[i,0]*x**i print('polinomio interpolación, con puntos: ', k) print(polinomio)