s1Eva_IT2018_T4 El gol imposible – Métodos numéricos

Ejercicio: 1Eva_IT2018_T4 El gol imposible

Tabla de datos:

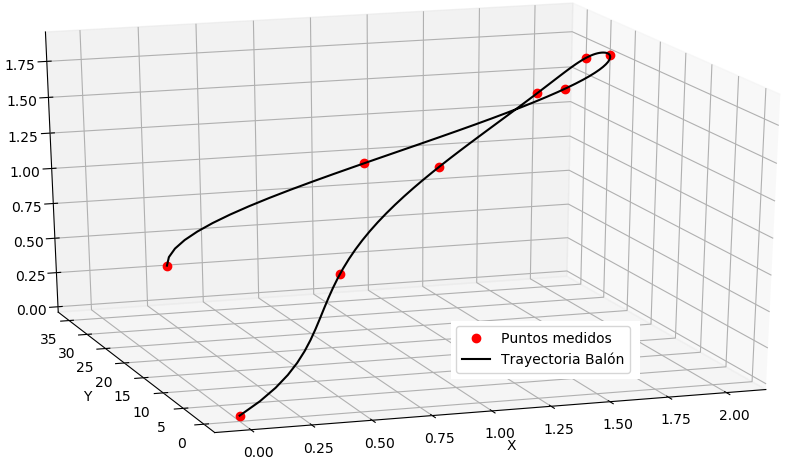
ti = [0.00, 0.15, 0.30, 0.45, 0.60, 0.75, 0.90, 1.05, 1.20]
xi = [0.00, 0.50, 1.00, 1.50, 1.80, 2.00, 1.90, 1.10, 0.30]
yi = [0.00, 4.44, 8.88,13.31,17.75,22.19,26.63,31.06,35.50]
zi = [0.00, 0.81, 1.40, 1.77, 1.91, 1.84, 1.55, 1.03, 0.30]

Observe que, un gol simplificado con física básica es un tiro parabólico cuya trayectoria se compone de movimientos en los ejes, Y y Z. Sin embargo, lo «imposible» del gol mostrado es añadir el movimiento en X. (Referencia de la imagen en el enunciado)

El movimiento de «profundidad» o dirección hacia el arco y(t) es semejante a un polinomio de primer grado, y el movimiento de «altura» z(t) es un polinomio de segundo grado. El movimiento «imposible» en el eje X, podría ser descrito por un polinomio de segundo o mayor grado.

a) Encontrar t para altura máxima, que se encuentra al igualar la derivada dz/dt a cero. Para interpolar el polinomio z(t), de segundo grado, se puede usar tres puntos de los sugeridos: 0, 0.3 y 0.6, que además son equidistantes en t (facilita usar cualquier método de interpolación).

Por ejemplo, con diferencias finitas avanzadas:

t	z(t)	d1	d2
0.00	0.00	1.40	-0.89
0.30	1.40	0.51
0.60	1.91

z(t) = 0 + 1.40\frac{(t-0)}{1!(0.3)} - 0.89 \frac{(t-0)(t-0.3)}{2!(0.3)^2}

= 0 + 4.66 t - 4.94(t^2-0.3t)

= 4.66 t + 1.48 t - 4.94 t^2

z(t) = 6.42 t - 4.94 t^2

para encontrar el valor máximo se encuentra $\frac{dz}{dt} = 0$

\frac{dz}{dt} = 6.42 - 2(4.94) t

6.42 - 2(4.94) t = 0

t = \frac{6.42}{2(4.94)}

t = 0.649

Observe que el resultado tiene sentido, pues según la tabla, el máximo debería estar entre 0.60 y 0.75

b) El cruce por la «barrera», corresponde al desplazamiento del balón en el eje Y a 9 metros: y(t) = 9.
El polinomio modelo de primer grado usa dos puntos para la interpolación, de los sugeridos se escogen dos, por ejemplo: 0.0 y 0.3.

Usando diferencias finitas avanzadas :

d1 = (8.88-0) = 8.88

y(t) = 0 + 8.88\frac{(t-0)}{1!(0.3)}

y(t) = 29.6 t

usando y(t) = 9

29.6 t = 9
t = 0.30
z(0.30) = 1.40
(de la tabla de datos)

cuya respuesta con solo dos dígitos decimales es coherente, al estar cercano el valor a una distancia y=8.88 o aproximado a 9.
La respuesta puede ser mejorada usando más digitos significativos en las operaciones.

c) La desviación máxima en eje X.
Determine un polinomio para la trayectoria en el eje X y obtenga el máximo igualando la derivada del polinomio x(t) a cero.

Por simplicidad, se usa un polinomio de segundo grado, alrededor de los valores máximos en el eje X

t	x(t)	d1	d2
0.60	1.80	0.20	-0.30
0.75	2.00	-0.10
0.90	1.90

x(t) = 1.80 + 0.20 \frac{(t-0.60)}{1!(0.15)} -0.30 \frac{(t-0.60)(t-0.75)}{2!(0.15)^2}

x(t) = 1.80 + 1.33 (t-0.60) - 6.67(t-0.60)(t-0.75)

como se busca el máximo, se usa la derivada $\frac{dx}{dt} = 0$

\frac{dx}{dt} = 1.33 - 6.67(2t +(-0.60-0.75))

1.33 - 13.34t + 9.00 = 0

-13.34t + 10.33 = 0

t = 0.77

x(0.77) = 1.80 + 1.33(0.77-0.60) - 6.67(0.77-0.60)(0.77-0.75)

x(0.77) = 2.003

lo que es coherente con la tabla para el eje x, pues el máximo registrado es 2, y el próximo valor es menor, la curva será decreciente.

Desarrollo extra para observar y verificar resultados:

Usando los puntos y un graficador 3D se puede observar la trayectoria:

Tarea: Realice el ejercicio usando los algoritmos en Python, muestre los polinomios obtenidos y compare.

Nota: La gráfica 3D presentada usa interpolación de Lagrange con todos los puntos. Realice las observaciones y recomendaciones necesarias y presente su propuesta como tarea.