s2Eva_IIT2007_T2_AN Lanzamiento vertical proyectil

Ejercicio: 2Eva_IIT2007_T2_AN Lanzamiento vertical proyectil

la ecuación del problema:

m \frac{\delta v}{\delta t} = -mg - kv|v|

se despeja:

\frac{\delta v}{\delta t} = -g - \frac{k}{m}v|v|

y usando los valores indicados en el enunciado:

\frac{\delta v}{\delta t} = -9,8 - \frac{0.002}{0.11}v|v|

con valores iniciales de:

t₀ = 0 , v₀ = 8 , h=0.2

Como muestra inicial, se usa Runge-Kutta de 2do Orden

iteración 1

K_1 = h\frac{\delta v}{\delta t}(0, 8) = 0.2[-9,8 - \frac{0.002}{0.11}8|8|] = -2.1927 K_2 = h\frac{\delta v}{\delta t}(0+0.2, 8 -2.1927 ) = 0.2[-9,8 - \frac{0.002}{0.11}(8 -2.1927)|8 -2.1927|] =-2.0826 v_1 = -9,8 +\frac{-2.1927-2.0826 }{2} = 5.8623 t_1 = t_0 + h = 0 + 0.2 = 0.2 error = O(h^3) = O(0.2^3) = O(0.008)

iteración 2

K_1 = h\frac{\delta v}{\delta t}(0.2, 5.8623) = 0.2[-9,8 - \frac{0.002}{0.11}(5.8623)|5.8623|] = -2.085 K_2 = h\frac{\delta v}{\delta t}(0+0.2, 5.8623 -2.085) = 0.2[-9,8 - \frac{0.002}{0.11}(5.8623 -2.085)|5.8623 -2.085|] =-2.0119 v_2 = -9,8 +\frac{-2.085-2.0119}{2} = 3.8139 t_2 = t_1 + h = 0.2 + 0.2 = 0.4

iteración 3

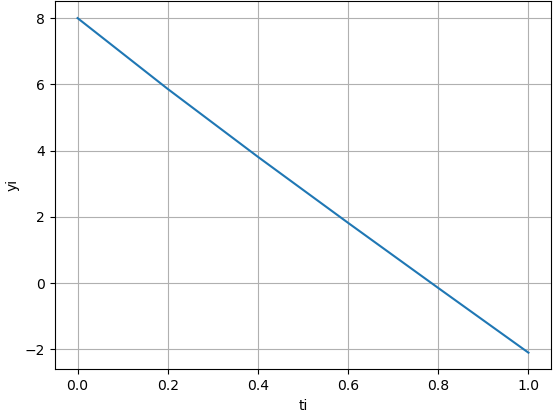
K_1 = h\frac{\delta v}{\delta t}(0.4, 3.8139) = 0.2[-9,8 - \frac{0.002}{0.11}( 3.8139)| 3.8139|] = -2.0129 K_2 = h\frac{\delta v}{\delta t}(0+0.2, 3.8139 -2.0129) = 0.2[-9,8 - \frac{0.002}{0.11}(3.8139 -2.0129)|3.8139 -2.0129|] =-1.9718 v_3 = -9,8 +\frac{-2.0129-1.9718}{2} = 1.8215 t_3 = t_2 + h = 0.4 + 0.2 = 0.6

---

Tabla y gráfica del ejercicio para todo el intervalo:

 [xi,      yi,     K1,     K2    ]
[[ 0.      8.      0.      0.    ]
 [ 0.2     5.8623 -2.1927 -2.0826]
 [ 0.4     3.8139 -2.085  -2.0119]
 [ 0.6     1.8215 -2.0129 -1.9718]
 [ 0.8    -0.1444 -1.9721 -1.9599]
 [ 1.     -2.0964 -1.9599 -1.9439]]

Algoritmo en Python

# 3Eva_IT2009_T2 EDO Taylor Seno(x)
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
d1y = lambda t,v: -9.8-(0.002/0.11)*v*np.abs(v)
x0 = 0
y0 = 8
h = 0.2
a = 0
b = 1

# PROCEDIMIENTO
muestras = int((b -a)/h)+1
tabla = np.zeros(shape=(muestras,4),dtype=float)

i = 0
xi = x0
yi = y0
tabla[i,:] = [xi,yi,0,0]

i = i+1
while not(i>=muestras):
    K1 = h*d1y(xi,yi)
    K2 = h*d1y(xi+h,yi+K1)
    yi = yi + (K1+K2)/2
    xi = xi +h
    tabla[i,:] = [xi,yi,K1,K2]
    i = i+1
# vector para gráfica
xg = tabla[:,0]
yg = tabla[:,1]

# SALIDA
# muestra 4 decimales
np.set_printoptions(precision=4)
print(' [xi, yi, K1, K2]')
print(tabla)
# Gráfica
plt.plot(xg,yg)
plt.xlabel('ti')
plt.ylabel('yi')
plt.grid()
plt.show()

Tarea: Realizar iteraciones para Runge-Kutta de 4to Orden