Ejercicio: 2Eva_IIT2016_T3_MN EDO Taylor 2, Tanque de agua
La solución obtenida se realiza con h=0.5 y usando dos métodos para comparar resultados.
\frac{dy}{dt} = -k \sqrt{y}1. EDO con Taylor
Usando una aproximación con dos términos de Taylor:
y_{i+1}=y_{i}+ y'_{i} h+\frac{y"_{i}}{2}h^{2}Por lo que se obtienen las derivadas necesarias:
y'_i= -k (y_i)^{1/2} y"_i= \frac{-k}{2}(y_i)^{-1/2}1.1 iteraciones
i=0, y0=3, t0=0
y'_0= -k(y_0)^{1/2} =-0.06(3)^{1/2} = -0.1039 y"_0= \frac{-0.06}{2}(3)^{-1/2} = -0.0173 y_{1}=y_{0}+ y'_{0} (1)+\frac{y"_{0}}{2}(1)^{2} y_{1}=3+ (-0.1039) (0.5)+\frac{-0.0173}{2}(0.5)^{2}= 2.9458t1=t0+h = 0+0.5= 0.5
i=1, y1=2.9458, t1=0.5
y'_1= -k(y_1)^{1/2} =-0.06(2.887)^{1/2} =-0.1029 y"_1= \frac{-0.06}{2}(2.887)^{-1/2} = -0.0174 y_{2}=y_{1}+ y'_{1} (1)+\frac{y"_{1}}{2}(1)^{2} y_{1}=2.9458+ (-0.1029) (1)+\frac{-0.0174}{2}(1)^{2}= 2.8921t2=t1+h = 0.5+0.5 = 1.0
i=2, y2=2.8921, t2=1.0
Resolver como Tarea
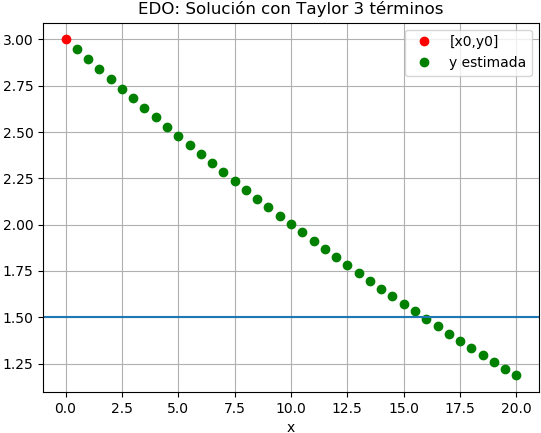
1.2 Resultados con Python
Realizando una tabla de valores usando Python y una gráfica, encuentra que el valor buscado del tanque a la mitad se obtiene en 16 minutos.
estimado[xi,yi] [[ 0. 3. ] [ 0.5 2.94587341] [ 1. 2.89219791] [ 1.5 2.83897347] [ 2. 2.7862001 ] ... [14. 1.65488507] [14.5 1.61337731] [15. 1.57231935] [15.5 1.53171109] [16. 1.49155239] [16.5 1.45184313] [17. 1.41258317] [17.5 1.37377234] [18. 1.33541049] [18.5 1.29749744] [19. 1.26003297] [19.5 1.22301689] [20. 1.18644897]]
Algoritmo en Python para Solución EDO con tres términos:
# EDO. Método de Taylor 3 términos # estima la solucion para muestras espaciadas h en eje x # valores iniciales x0,y0 # entrega arreglo [[x,y]] import numpy as np def edo_taylor3t(d1y,d2y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,2),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0] x = x0 y = y0 for i in range(1,tamano,1): y = y + h*d1y(x,y) + ((h**2)/2)*d2y(x,y) x = x+h estimado[i] = [x,y] return(estimado) # PROGRAMA PRUEBA # 2Eva_IIT2016_T3_MN EDO Taylor 2, Tanque de agua # INGRESO. k=0.06 # d1y = y' = f, d2y = y'' = f' d1y = lambda x,y: -k*(y**0.5) d2y = lambda x,y: -(k/2)*(y**(-0.5)) x0 = 0 y0 = 3 h = 1/2 muestras = 40 # PROCEDIMIENTO puntos = edo_taylor3t(d1y,d2y,x0,y0,h,muestras) xi = puntos[:,0] yi = puntos[:,1] # SALIDA print('estimado[xi,yi]') print(puntos) # Gráfica import matplotlib.pyplot as plt plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]') plt.plot(xi[1:],yi[1:],'o', color='g', label ='y estimada') plt.axhline(y0/2) plt.title('EDO: Solución con Taylor 3 términos') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid() plt.show()
2. EDO con Runge-Kutta de 2do Orden dy/dx
Para éste método no se requiere desarrollar la segunda derivada, se usa el mismo h =0.5 con fines de comparación de resultados
2.1 ITeraciones
i = 1, y0=3, t0=0
K_1 = h y'(x_0,y_0) = (0.5)*(-0.06)(3)^{1/2} =-0.05196 K_2 = h y'(x_0+h,y_0+K_1) = (0.5)* y'(0.5,3-0.05196) = -0.05150 y_1 = y_0+\frac{K1+K2}{2} = 3+\frac{-0.05196-0.05150}{2} = 2.9482i = 2, y1=2.9482, t1=0.5
K_1 = h y'(x_1,y_1) = (0.5)*(-0.06)(2.9482)^{1/2} =-0.05149 K_2 = h y'(x_1+h,y_1+K_1) = (0.5)* y'(0.5,2.9482-0.05149) = -0.05103 y_1 = y_0+\frac{K1+K2}{2} = 3+\frac{-0.05149-0.05103}{2} = -2.8946i = 3, y1=2.8946, t1=1.0
Resolver como Tarea
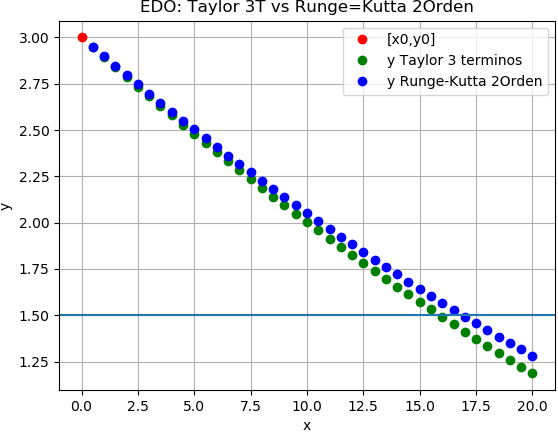
2.2 Resultados con Python
Si comparamos con los resultados anteriores en una tabla, y obteniendo las diferencias entre cada iteración se tiene que:
estimado[xi,yi Taylor, yi Runge-Kutta, diferencias] [[ 0.0 3.00000000 3.00000000 0.00000000e+00] [ 0.5 2.94587341 2.94826446 -2.39104632e-03] [ 1.0 2.89219791 2.89697892 -4.78100868e-03] [ 1.5 2.83897347 2.84614338 -7.16990106e-03] [ 2.0 2.78620010 2.79575783 -9.55773860e-03] ... [ 14.0 1.65488507 1.72150488 -6.66198112e-02] [ 14.5 1.61337731 1.68236934 -6.89920328e-02] [ 15.0 1.57231935 1.64368380 -7.13644510e-02] [ 15.5 1.53171109 1.60544826 -7.37371784e-02] [ 16.0 1.49155239 1.56766273 -7.61103370e-02] [ 16.5 1.45184313 1.53032719 -7.84840585e-02] [ 17.0 1.41258317 1.49344165 -8.08584854e-02] [ 17.5 1.37377234 1.45700611 -8.32337718e-02] [ 18.0 1.33541049 1.42102058 -8.56100848e-02] [ 18.5 1.29749744 1.38548504 -8.79876055e-02] [ 19.0 1.26003297 1.35039950 -9.03665304e-02] [ 19.5 1.22301689 1.31576397 -9.27470733e-02] [ 20.0 1.18644897 1.28157843 -9.51294661e-02]] error en rango: 0.09512946613018003
# EDO. Método de Taylor 3 términos # estima la solucion para muestras espaciadas h en eje x # valores iniciales x0,y0 # entrega arreglo [[x,y]] import numpy as np def edo_taylor3t(d1y,d2y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,2),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0] x = x0 y = y0 for i in range(1,tamano,1): y = y + h*d1y(x,y) + ((h**2)/2)*d2y(x,y) x = x+h estimado[i] = [x,y] return(estimado) def rungekutta2(d1y,x0,y0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,2),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0] xi = x0 yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (K1+K2)/2 xi = xi + h estimado[i] = [xi,yi] return(estimado) # PROGRAMA PRUEBA # 2Eva_IIT2016_T3_MN EDO Taylor 2, Tanque de agua # INGRESO. k=0.06 # d1y = y' = f, d2y = y'' = f' d1y = lambda x,y: -k*(y**0.5) d2y = lambda x,y: -(k/2)*(y**(-0.5)) x0 = 0 y0 = 3 h = 1/2 muestras = 40 # PROCEDIMIENTO puntos = edo_taylor3t(d1y,d2y,x0,y0,h,muestras) xi = puntos[:,0] yi = puntos[:,1] # Con Runge Kutta puntosRK2 = rungekutta2(d1y,x0,y0,h,muestras) xiRK2 = puntosRK2[:,0] yiRK2 = puntosRK2[:,1] # diferencias diferencias = yi-yiRK2 error = np.max(np.abs(diferencias)) tabla = np.copy(puntos) tabla = np.concatenate((puntos,np.transpose([yiRK2]), np.transpose([diferencias])), axis = 1) # SALIDA print('estimado[xi,yi Taylor,yi Runge-Kutta,diferencias]') print(tabla) print('error en rango: ', error) # Gráfica import matplotlib.pyplot as plt plt.plot(xi[0],yi[0],'o', color='r', label ='[x0,y0]') plt.plot(xi[1:],yi[1:],'o', color='g', label ='y Taylor 3 terminos') plt.plot(xiRK2[1:],yiRK2[1:],'o', color='blue', label ='y Runge-Kutta 2Orden') plt.axhline(y0/2) plt.title('EDO: Taylor 3T vs Runge=Kutta 2Orden') plt.xlabel('x') plt.ylabel('y') plt.legend() plt.grid() plt.show()