s2Eva_IIT2017_T1 EDO Runge Kutta 2do Orden d2y/dx2

Ejercicio: 2Eva_IIT2017_T1 EDO Runge Kutta 2do Orden d2y/dx2

Tema 1

Runge kutta de 2do Orden
f: y' = z
g: z' = .....
K1y = h f(xi, yi, zi)
K1z = h g(xi, y1, zi)

K2y = h f(xi+h, yi+K1y, zi+K1z)
K2z = h g(xi+h, yi+K1y, zi+K1z)

y(i+1) = yi + (1/2)(K1y + K2y)
z(i+1) = zi + (1/2)(K1z + K2z)

x(i+1) = xi + h
E = O(h³) 
xi ≤ z ≤ x(i+1)

f: z = Θ’
g: z’ = (-gr/L) sin(Θ)

Θ(0) = π/6
z(0) = 0

h=0.1

i=0, t0 = 0, Θ0 = π/6, z0 = 0
    K1y = 0.1(0) = 0
    K1z = 0.1(-9.8/2)sin(π/6) = -0.245

    K2y = 0.1(0+(-0.245)) = -0.0245
    K2z = 0.1(-9.8/2)sin(π/6+0) = -0.245

    Θ1 = π/6 + (1/2)(0+(-0.0245)) = 0.51139
    z1 = 0 + (1/2)(-0.245-0.245) = -0.245
    t1 = 0 + 0.1 = 0.1

i=1, t1 = 0.1, Θ1 = 0.51139, z1 = -0.245
    K1y = 0.1(-0.245) = -0.0245
    K1z = 0.1(-9.8/2)sin(0.51139) = -0.23978

    K2y = 0.1(-0.245+(-0.0245)) = -0.049
    K2z = 0.1(-9.8/2)sin(0.51139+(-0.0245)) = -0.22924

    Θ2 = 0.51139 + (1/2)(-0.0245+(-0.049)) = 0.47509
    z2 = -0.245 + (1/2)(-0.23978+(-0.22924)) = -0.245
    t2 = 0.1 + 0.1 = 0.2

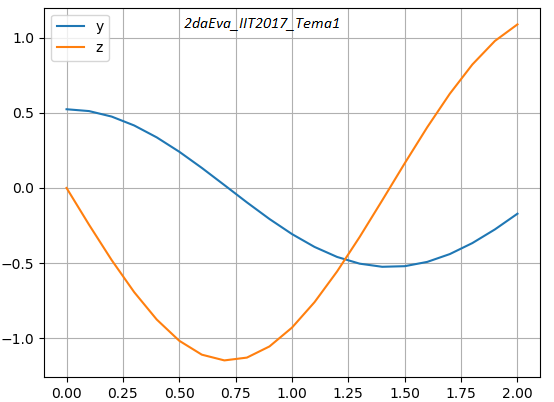
   t         theta     z
[[ 0.        0.523599  0.      ]
 [ 0.1       0.511349 -0.245   ]
 [ 0.2       0.47486  -0.479513]
 [ 0.3       0.415707 -0.692975]
 [ 0.4       0.336515 -0.875098]
 [ 0.5       0.240915 -1.016375]
 [ 0.6       0.133432 -1.108842]
 [ 0.7       0.019289 -1.14696 ]
 [ 0.8      -0.09588  -1.128346]
 [ 0.9      -0.206369 -1.054127]
 [ 1.       -0.306761 -0.92877 ]
 [ 1.1      -0.39224  -0.759461]
 [ 1.2      -0.458821 -0.555246]
 [ 1.3      -0.503495 -0.326207]
 [ 1.4      -0.524294 -0.082851]
 [ 1.5      -0.520315  0.164197]
 [ 1.6      -0.491715  0.404296]
 [ 1.7      -0.439718  0.62682 ]
 [ 1.8      -0.366606  0.821313]
 [ 1.9      -0.275693  0.977893]
 [ 2.       -0.171235  1.087942]]

Literal b), con h= 0.25, con t = 1 ángulo= -0.352484

   t         theta     z
[[ 0.        0.523599  0.      ]
 [ 0.25      0.447036 -0.6125  ]
 [ 0.5       0.227716 -1.054721]
 [ 0.75     -0.070533 -1.170971]
 [ 1.       -0.352484 -0.910162]
 [ 1.25     -0.527161 -0.363031]
 [ 1.5      -0.540884  0.299952]
 [ 1.75     -0.387053  0.890475]
 [ 2.       -0.106636  1.221932]]

El error de del orden h³

Instruccciones en python, usando el algoritmo desarrollado en clase

# Runge Kutta de 2do
# EDO de 2do orden con condiciones de inicio
import numpy as np
import matplotlib.pyplot as plt

def rungekutta2_fg(f,g,v0,h,m):
    tabla = [v0]
    xi = v0[0]
    yi = v0[1]
    zi = v0[2]
    for i in range(0,m,1):
        K1y = h * f(xi,yi,zi)
        K1z = h * g(xi,yi,zi)
        
        K2y = h * f(xi+h, yi + K1y, zi+K1z)
        K2z = h * g(xi+h, yi + K1y, zi+K1z)

        yi1 = yi + (1/2)*(K1y+K2y)
        zi1 = zi + (1/2)*(K1z+K2z)
        xi1 = xi + h
        vector = [xi1,yi1,zi1]
        tabla.append(vector)

        xi = xi1
        yi = yi1
        zi = zi1
    tabla = np.array(tabla)
    return(tabla)

# Programa Prueba
# Funciones
f = lambda x,y,z : z
g = lambda x,y,z : (-gr/L)*np.sin(y)

gr = 9.8
L = 2

x0 = 0
y0 = np.pi/6
z0 = 0

v0 = [x0,y0,z0]

h = 0.1
xn = 2
m = int((xn-x0)/h)

# PROCEDIMIENTO
tabla = rungekutta2_fg(f,g,v0,h,m)

xi = tabla[:,0]
yi = tabla[:,1]
zi = tabla[:,2]

# SALIDA
np.set_printoptions(precision=6)
print('x, y, z')
print(tabla)
plt.plot(xi,yi, label='y')
plt.plot(xi,zi, label='z')
plt.legend()
plt.grid()
plt.show()