s2Eva_IIT2017_T4 Problema con valor de frontera

Ejercicio: 2Eva_IIT2017_T4 Problema con valor de frontera

\frac{d^2T}{dx^2} + \frac{1}{x}\frac{dT}{dx} +S =0 0 \leq x \leq 1

Las diferencias finitas a usar son:

\frac{dT}{dx} =\frac{T_{i+1} - T_{i-1}}{2h}+O(h^2) \frac{d^2T}{dx^2}=\frac{T_{i+1} - 2T_i + T_{i-1}}{h^2}+O(h^2)

que al reemplazar el la ecuación:

\frac{T_{i+1} - 2T_i + T_{i-1}}{h^2} + \frac{1}{x_i}\frac{T_{i+1} -T_{i-1}}{2h}+S=0 2x_i (T_{i+1} - 4h x_i T_i + T_{i-1}) + h (T_{i+1} - T_{i-1}) = -2h^2 S x_i T_{i+1}(2x_i + h) - 4x_i T_i + T_{i-1}(2x_i - h) = -2h^2 S x_i T_{i-1}(2x_i - h) - 4x_i T_i + T_{i+1}(2x_i + h)= -2h^2 S x_i

con lo que se puede crear un sistema de ecuaciones para cada valor xi con T₀=2 y T₄ =1 que son parte del enunciado del problema.

Siendo h = 0.25 = 1/4,  y se indica al final que S=1, se crea un sistema de ecuaciones a resolver,

x = [0, 1/4, 1/4, 3/4, 1]

T_{i-1}\Big[2x_i - \frac{1}{4} \Big] - 4x_i T_i + T_{i+1}\Big[2x_i + \frac{1}{4} \Big] = -2\Big(\frac{1}{4}\Big)^2 (1) x_i T_{i-1}\Big[2x_i -\frac{1}{4}\Big] - 4x_i T_i + T_{i+1}\Big[2x_i + \frac{1}{4}\Big] = -\frac{1}{8} x_i

se sustituye con los valores conocidos para cada i:

i=1: 
T0[2(1/4) - 1/4] - 4(1/4)T1 + T2[2(1/4) + 1/4] = -(1/8)(1/4)

     - T1 + (3/4)T2 = -1/32 - (1/4)(2)
     - T1 + (3/4)T2 = -17/32

i=2: 
T1[2(1/2) - 1/4] - 4(1/2)T2 + T3[2(1/2) + 1/4] = -(1/8)(1/2)

     (3/4)T1 - 2T2 + (5/4)T3 = -1/16

i=3: 
T2[2(3/4) - 1/4] - 4(3/4)T3 + T4[2(3/4) + 1/4] = -(1/8)(3/4)

     (5/4)T2 - 3T3 = -3/32 - (7/4)(1)
     (5/4)T2 - 3T3 = -59/32

se ponen las ecuaciones en matrices para resolver con algun metodo numérico:

A = [[ -1, 3/4,   0],
     [3/4,  -2, 5/4],
     [  0, 5/4,  -3]]
B = [-17/32, -1/16, -59/32]
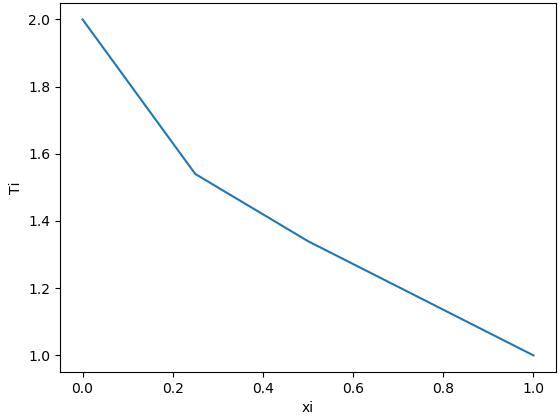
np.linalg.solve(A,B)
array([ 1.54,  1.34,  1.17])