Ejercicio: 2Eva_IIT2018_T2 Kunge Kutta 2do Orden x»
\frac{\delta ^2 x}{\delta t^2} + 5t\frac{\delta x}{\delta t} +(t+7)\sin (\pi t) = 0 x'' + 5tx' +(t+7)\sin (\pi t) = 0 x'' = -5tx' -(t+7)\sin (\pi t) = 0si se usa z=x’
z' = -5tz -(t+7)\sin (\pi t) = 0se convierte en:
f(t,x,z) = x' = z g(t,x,z) = x'' = z' = -5tz -(t+7)sin (\pi t) = 0Tarea: Desarrollar 3 iteraciones en Papel.
Donde se aplica el algoritmo de Runge Kutta
http://blog.espol.edu.ec/analisisnumerico/8-2-2-runge-kutta-d2y-dx2/
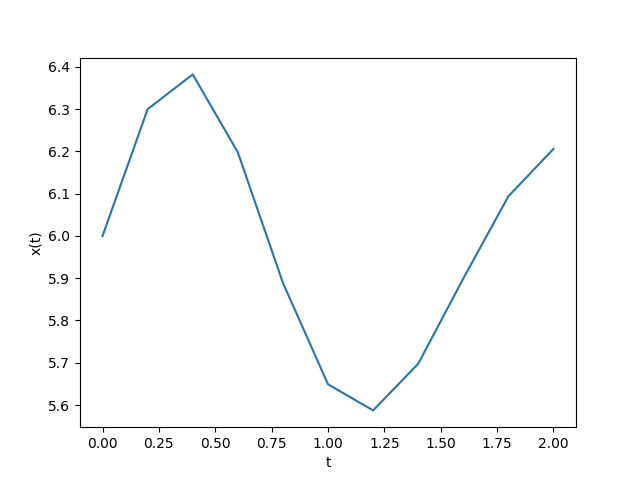
t, x, z [[ 0. 6. 1.5 ] [ 0.2 6.3 0.92679462] [ 0.4 6.38218195 -0.27187703] [ 0.6 6.19792527 -1.17287944] [ 0.8 5.88916155 -1.23638799] [ 1. 5.6491005 -0.61819399] [ 1.2 5.5872811 0.17288691] [ 1.4 5.69750883 0.69945284] [ 1.6 5.8992535 0.77223688] [ 1.8 6.09372469 0.43437943] [ 2. 6.20586248 -0.12630953]]
Instrucciones en Python
# 2Eva_IIT2018_T2 Kunge Kutta 2do Orden x'' import numpy as np def rungekutta2_fg(f,g,x0,y0,z0,h,muestras): tamano = muestras + 1 estimado = np.zeros(shape=(tamano,3),dtype=float) # incluye el punto [x0,y0] estimado[0] = [x0,y0,z0] xi = x0 yi = y0 zi = z0 for i in range(1,tamano,1): K1y = h * f(xi,yi,zi) K1z = h * g(xi,yi,zi) K2y = h * f(xi+h, yi + K1y, zi + K1z) K2z = h * g(xi+h, yi + K1y, zi + K1z) yi = yi + (K1y+K2y)/2 zi = zi + (K1z+K2z)/2 xi = xi + h estimado[i] = [xi,yi,zi] return(estimado) # PROGRAMA # INGRESO f = lambda t,x,z: z g = lambda t,x,z: -5*t*z-(t+7)*np.sin(np.pi*t) t0 = 0 x0 = 6 z0 = 1.5 h = 0.2 muestras = 10 # PROCEDIMIENTO tabla = rungekutta2_fg(f,g,t0,x0,z0,h,muestras) # SALIDA print(tabla) # GRAFICA import matplotlib.pyplot as plt plt.plot(tabla[:,0],tabla[:,1]) plt.xlabel('t') plt.ylabel('x(t)') plt.show()