Ejercicio: 2Eva_IIT2018_T3 EDP
Se indica en el enunciado que b = 0
simplificando la ecuación a:
\frac{\delta u}{\delta t} = \frac{\delta ^2 u}{\delta x^2}Reordenando la ecuación a la forma estandarizada:
\frac{\delta ^2 u}{\delta x^2} = \frac{\delta u}{\delta t}Seleccione un método: explícito o implícito.
Si el método es explícito, las diferencias finitas a usar son hacia adelante y centrada:
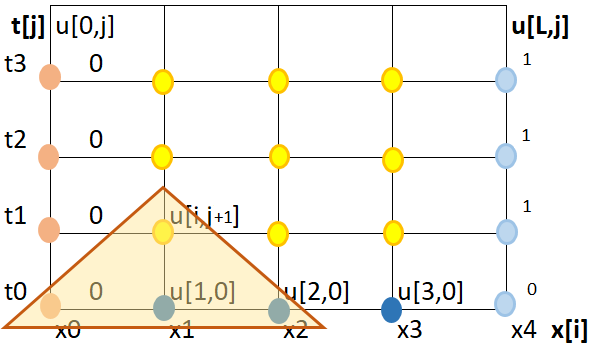
como referencia se usa la gráfica.
Se selecciona la esquina inferior derecha como 0, por la segunda ecuación de condiciones y facilidad de cálculo. (No hubo indicación durante el examen que muestre lo contrario)
condiciones de frontera U(0,t)=0, U(1,t)=1 condiciones de inicio U(x,0)=0, 0≤x≤1
aunque lo más recomendable sería cambiar la condición de inicio a:
condiciones de inicio U(x,0)=0, 0<x<1
Siguiendo con el tema de la ecuación, al reemplazar las diferencias finitas en la ecuación:
\frac{U(x_{i+1},t_j)-2U(x_{i},t_j)+U(x_{i-1},t_j)}{\Delta x^2} = = \frac{U(x_i,t_{j+1})-U(x_i,t_j)}{\Delta t}
se reagrupan los términos que son constantes y los términos de error se acumulan:
\frac{\Delta t}{\Delta x^2} \Big[U(x_{i+1},t_j)-2U(x_i,t_j)+U(x_{i-1},t_j) \Big] = U(x_i,t_{j+1})-U(x_i,t_j)siendo,
\lambda= \frac{\Delta t}{\Delta x^2} error \cong O(\Delta t) + O(\Delta x^2)continuando con la ecuación, se simplifica la escritura usando sólo los índices i,j y se reordena de izquierda a derecha como en la gráfica
\lambda \Big[U[i-1,j]-2U[i,j]+U[i+1,j] \Big] = U[i,j+1]-U]i,j] \lambda U[i-1,j]+(-2\lambda+1)U[i,j]+\lambda U[i+1,j] = U[i,j+1] U[i,j+1] = \lambda U[i-1,j]+(-2\lambda+1)U[i,j]+\lambda U[i+1,j] U[i,j+1] = P U[i-1,j]+QU[i,j]+R U[i+1,j] P=R = \lambda Q = -2\lambda+1En las iteraciones, el valor de P,Q y R se calculan a partir de λ ≤ 1/2
iteraciones: j=0, i=1
U[1,1] = P*0+Q*0+R*0 = 0
j=0, i=2
U[2,1] = P*0+Q*0+R*0=0
j=0, i=3
U[3,1] = P*0+Q*0+R*1=R=\lambda=\frac{1}{2}iteraciones: j=1, i=1
U[1,2] = P*0+Q*0+R*0 = 0
j=1, i=2
U[2,2] = P*0+Q*0+R*\lambda = \lambda ^2 = \frac{1}{4}j=1, i=3
U[3,2] = P*0+Q*\frac{1}{4}+R (\lambda) U[3,2] = (-2\lambda +1) \frac{1}{4}+\lambda^2 = \Big(-2\frac{1}{2}+1\Big) \frac{1}{4}+\Big(\frac{1}{2}\Big)^2 U[3,2] =0\frac{1}{4} + \frac{1}{4} = \frac{1}{4}Literal b. Para el cálculo del error:
\lambda \leq \frac{1}{2} \frac{\Delta t}{\Delta x^2} \leq \frac{1}{2} \Delta t \leq \frac{\Delta x^2}{2}en el enunciado se indica h = 0.25 = ¼ = Δ x
\Delta t \leq \frac{(1/4)^2}{2} = \frac{1}{32} error \cong O(\Delta t) + O(\Delta x^2) error \cong \frac{\Delta x^2}{2}+ \Delta x^2 error \cong \frac{3}{2}\Delta x^2 error \cong \frac{3}{2}( \frac{1}{4})^2 error \cong \frac{3}{32} = 0.09375