Ejercicio: 2Eva_IT2018_T1 EDO Paracaidista wingsuit
Plantear con: [ Runge-Kutta para f''(x) ] [ Runge-Kutta para f'(x) ]
a. Planteamiento con Runge-Kutta 2do Orden para Segunda derivada
La expresión:
\frac{dv}{dt} = g - \frac{cd}{m} v^2se puede plantear sustituir la variable con v = -\frac{dy}{dt} al considerar el sentido contrario entre la velocidad al caer y la referencia de altura hacia arriba. Ver figura.
\frac{d^2y}{dt^2} = g - \frac{cd}{m} \Big( \frac{dy}{dt} \Big) ^2Que es una EDO de 2do orden o como 2da derivada.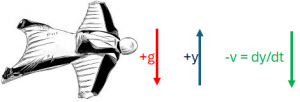
La solución se propone resolver de forma simultanea para t,y,v con Runge Kutta para segunda derivada donde:
f(t,y,v) = -v g(t,y,v) = g - \frac{cd}{m} v^2Al sustituir los valores de las constantes en la ecuación como gravedad, masa e índice de arrastre se tiene:
f(t,y,v) = -v g(t,y,v) = 9.8 - \frac{0.225}{90} v^2con las condiciones iniciales del ejercicio t0 = 0 , y0 = 1000, v0 = 0
la velocidad se inicia con cero, si el paracaidista se deja caer desde el borde el risco, como en el video adjunto al enunciado.
Para las iteraciones, recuerde que
t se corrige con t+h (en el algoritmo era la posición para x)
y se corrige con y+K1y
v se corrige con v+K1v (en el algoritmo era la posición para z)
itera = 0
K1y = h f(t,y,v) = 2(-(0)) = 0 K1v = h g(t,y,v) = 2(9.8 - \frac{0.225}{90} (0)^2) = 19.6..
K2y = h f(t+h, y+K1y, v + K1v) = 2(-(0 + 19.6)) = -39.2
..
y_1 = y_0 + \frac{K1y+K2y}{2} = 1000 + \frac{0-39.2}{2}= 980.4
| ti | yi | vi | K1y | K1v | K2y | K2v |
| 0 | 1000 | 0 | 0 | 0 | 0 | 0 |
| 2 | 980.4 | 18.63 | 0 | 19.6 | -39.2 | 17.6792 |
itera = 1
K1y = 2(-(18.63)) = -37.2792 K1v = 2(9.8 - \frac{0.225}{90} (18.63)^2) = 17.8628..
K2y =2(-(18.6396+17.8628)) =-73.00
..
y_2 =980.4 + \frac{ -37.2792+(-73.00)}{2}= 925.25
| ti | yi | vi | K1y | K1v | K2y | K2v |
| 0 | 1000 | 0 | 0 | 0 | 0 | 0 |
| 2 | 980.4 | 18.63 | 0 | 19.6 | -39.2 | 17.6792 |
| 4 | 925.25 | 34.0399 | -37.2792 | 17.8628 | -73.00 | 12.9378 |
itera = 2
K1y = h f(t,y,v) = 2(-(34.0399)) = -68.0798 K1v = h g(t,y,v) = 2(9.8 - \frac{0.225}{90} (34.0399)^2) = 13.8064..
K2y = h f(t+h, y+K1y, v + K1v) = 2(-(34.0399+13.8064)) =-95.6927
..
y_2 = 925.25 + \frac{ -68.0798+(-95.6927)}{2}= 843.3716
| ti | yi | vi | K1y | K1v | K2y | K2v |
| 0 | 1000 | 0 | 0 | 0 | 0 | 0 |
| 2 | 980.4 | 18.63 | 0 | 19.6 | -39.2 | 17.6792 |
| 4 | 925.25 | 34.0399 | -37.2792 | 17.8628 | -73.00 | 12.9378 |
| 6 | 843.3716 | 45.0199 | -68.0798 | 13.8064 | -95.6927 | 8.1536 |
Algoritmo con Python
Resultados
La velocidad máxima, si no hubiese límite en la altura, se encuentra en alrededor de 62.39 m/s.
Sin embargo, luego de 20 segundos se observa que la altura alcanza el valor de cero, es decir se alcanzó tierra con velocidad de 62 m/s, que son algo mas de 223 Km/h, el objeto se estrella...!
Resultados con el algoritmo:
Runge-Kutta Segunda derivada i [ xi, yi, zi ] [ K1y, K1z, K2y, K2z ] 0 [ 0. 1000. 0.] [0. 0. 0. 0.] 1 [ 2. 980.4 18.6396] [ 0. 19.6 -39.2 17.6792] 2 [ 4. 925.257973 34.039945] [-37.2792 17.862827 -73.004853 12.937864] 3 [ 6. 843.371672 45.019966] [-68.079891 13.806411 -95.692712 8.153631] 4 [ 8. 743.865726 52.131168] [ -90.039933 9.466013 -108.971959 4.75639 ] 5 [ 10. 633.591684 56.485537] [-104.262336 6.011707 -116.285749 2.697031] 6 [ 12. 516.97369 59.069216] [-112.971073 3.646921 -120.264915 1.520438] 7 [ 14. 396.681119 60.575537] [-118.138432 2.154139 -122.446709 0.858504] 8 [ 16. 274.277023 61.445121] [-121.151075 1.253021 -123.657117 0.486147] 9 [ 18. 150.664295 61.944336] [-122.890243 0.722485 -124.335213 0.275943] 10 [20. 26.361127 62.230024] [-123.888671 0.414496 -124.717664 0.15688 ] 11 [ 22. -98.336041 62.393224] [-1.244600e+02 2.371205e-01 -1.249343e+02 8.927924e-02] 12 [ 24. -223.257917 62.486357] [-1.247864e+02 1.354280e-01 -1.250573e+02 5.083841e-02] 13 [ 26. -348.307907 62.539475] [-1.249727e+02 7.727584e-02 -1.251273e+02 2.895913e-02] 14 [ 28. -473.430927 62.56976 ] [-1.250789e+02 4.407055e-02 -1.251671e+02 1.649935e-02] 15 [ 30. -598.595572 62.587023] [-1.251395e+02 2.512592e-02 -1.251898e+02 9.401535e-03] 16 [ 32. -723.783942 62.596863] [-1.251740e+02 1.432256e-02 -1.252027e+02 5.357469e-03] >>>
Instrucciones en Python
# 2Eva_IT2018_T1 Paracaidista wingsuit import numpy as np import matplotlib.pyplot as plt def rungekutta2_fg(f,g,x0,y0,z0,h,muestras, vertabla=False, precision = 6): ''' solucion a EDO con Runge-Kutta 2do Orden Segunda derivada, x0,y0 son valores iniciales, h es tamano de paso, muestras es la cantidad de puntos a calcular. ''' tamano = muestras + 1 tabla = np.zeros(shape=(tamano,3+4),dtype=float) # incluye el punto [x0,y0,z0] tabla[0] = [x0,y0,z0,0,0,0,0] xi = x0 yi = y0 zi = z0 i=0 if vertabla==True: print('Runge-Kutta Segunda derivada') print('i ','[ xi, yi, zi',']') print(' [ K1y, K1z, K2y, K2z ]') np.set_printoptions(precision) print(i,tabla[i,0:3]) print(' ',tabla[i,3:]) for i in range(1,tamano,1): K1y = h * f(xi,yi,zi) K1z = h * g(xi,yi,zi) K2y = h * f(xi+h, yi + K1y, zi + K1z) K2z = h * g(xi+h, yi + K1y, zi + K1z) yi = yi + (K1y+K2y)/2 zi = zi + (K1z+K2z)/2 xi = xi + h tabla[i] = [xi,yi,zi,K1y,K1z,K2y,K2z] if vertabla==True: txt = ' ' if i>=10: txt=' ' print(str(i)+'',tabla[i,0:3]) print(txt,tabla[i,3:]) return(tabla) # PROGRAMA PRUEBA # INGRESO f = lambda t,y,v: -v # el signo, revisar diagrama cuerpo libre g = lambda t,y,v: 9.8 - (0.225/90)*(v**2) t0 = 0 y0 = 1000 v0 = 0 h = 2 muestras = 15+1 # PROCEDIMIENTO tabla = rungekutta2_fg(f,g,t0,y0,v0,h,muestras, vertabla=True) ti = tabla[:,0] yi = tabla[:,1] vi = tabla[:,2] # SALIDA # print('tabla de resultados') # print(tabla) # GRAFICA plt.subplot(211) plt.plot(ti,vi,label='velocidad v(t)', color='green') plt.plot(ti,vi,'o') plt.ylabel('velocidad (m/s)') plt.title('paracaidista Wingsuit con Runge-Kutta') plt.legend() plt.grid() plt.subplot(212) plt.plot(ti,yi,label='Altura y(t)',) plt.plot(ti,yi,'o',) plt.axhline(0, color='red') plt.xlabel('tiempo (s)') plt.ylabel('Altura (m)') plt.legend() plt.grid() plt.show()
Plantear con: [ Runge-Kutta para f''(x) ] [ Runge-Kutta para f'(x) ]
b. Usando Runge-Kutta 2do Orden para Primera Derivada o velocidad,
El problema para un tiempo de observación t>0, se puede dividir en dos partes: velocidad y altura.
- Determinar velocidad: Se aplica Runge-Kutta a la expresión con primera derivada o velocidad. Use los valores iniciales dados, descarte calcular las alturas.
- Determinar las altura: Con los valores de velocidades y la altura inicial de 1 km = 1000 m puede integrar con trapecio para obtener la tabla de alturas. Se integra tramo a tramo.
 Observe las unidades de medida y que la velocidad es contraria al eje de altura dy/dt = -v.
Observe las unidades de medida y que la velocidad es contraria al eje de altura dy/dt = -v.
La expresión:
\frac{dv}{dt} = g - \frac{cd}{m} v^2 f(t,v) = g - \frac{cd}{m} v^2itera = 0
K1v = h f(t,v) = 2(9.8)- \frac{0.225}{90}(0)^2) = 19.6 K2v = h f(t+h , v + K1v) = 2( 9.8 - \frac{0.225}{90}(0+19.6)^2) = 17.6792 v_1 = v_0 + \frac{K1y+K2y}{2} = 0 + \frac{19.6+17.6792}{2}= 18.6396 t_1 =t_0 + h = 0+2 = 2itera = 1
K1v = 2(9.8 - \frac{0.225}{90} (18.6396)^2) = 17.8628 K2v = 2( 9.8 - \frac{0.225}{90} (18.6396+17.8628)^2) = 12.9379 v_1 = 18.6396 + \frac{17.8628+12.9379}{2}= 34.0399 t_1 =2+2 = 4itera = 2
K1v = 2(9.8 - \frac{0.225}{90} (34.0399)^2) = 13.8064 K2v = 2( 9.8 - \frac{0.225}{90} (34.0399+13.8064)^2) = 8.1536 v_1 = 34.0399 + \frac{13.8064+8.1536}{2}= 45.02 t_1 = 4+2 = 6las siguientes iteraciones se completan con el algoritmo.
Resultados
La velocidad máxima, si no hubiese límite en la altura, se encuentra en alrededor de 62.39 m/s.
Sin embargo, luego de 20 segundos se observa que la altura alcanza el valor de cero, es decir se alcanzó tierra con velocidad de 62 m/s, que son algo mas de 223 Km/h, el objeto se estrella...!
velocidad con Runge-Kutta primera derivada [tiempo, velocidad, K1,K2] [[ 0. 0. 0. 0. ] [ 2. 18.6396 19.6 17.6792] [ 4. 34.0399 17.8628 12.9379] [ 6. 45.02 13.8064 8.1536] [ 8. 52.1312 9.466 4.7564] [10. 56.4855 6.0117 2.697 ] [12. 59.0692 3.6469 1.5204] [14. 60.5755 2.1541 0.8585] [16. 61.4451 1.253 0.4861] [18. 61.9443 0.7225 0.2759] [20. 62.23 0.4145 0.1569] [22. 62.3932 0.2371 0.0893]] velocidad con RK2 y altura con trapecio [tiempo, velocidad, altura] [[ 0. 0. 1000. ] [ 2. 18.64 981.36] [ 4. 34.04 928.68] [ 6. 45.02 849.62] [ 8. 52.13 752.47] [ 10. 56.49 643.85] [ 12. 59.07 528.3 ] [ 14. 60.58 408.65] [ 16. 61.45 286.63] [ 18. 61.94 163.24] [ 20. 62.23 39.07] [ 22. 62.39 -85.55]] >>>
Los cálculos se realizaron usando las instrucciones en Python:
# 2da Evaluación I Término 2018 # Tema 1. Paracaidista wingsuit import numpy as np def rungekutta2(d1y,x0,y0,h,muestras): # Runge Kutta de 2do orden tamano = muestras + 1 tabla = np.zeros(shape=(tamano,2+2),dtype=float) # incluye el punto [x0,y0] tabla[0] = [x0,y0,0,0] xi = x0 yi = y0 for i in range(1,tamano,1): K1 = h * d1y(xi,yi) K2 = h * d1y(xi+h, yi + K1) yi = yi + (1/2)*(K1+K2) xi = xi + h tabla[i] = [xi,yi,K1,K2] return(tabla) def integratrapecio_fi_tabla(xi,fi,y0): tamano = len(xi) yi = np.zeros(tamano,dtype = float) yi[0] = y0 for i in range(1,tamano,1): h = xi[i]-xi[i-1] trapecio = h*(fi[i]+fi[i-1])/2 yi[i]= yi[i-1] + trapecio return(yi) # PROGRAMA ------------------------- # INGRESO g = 9.8 cd = 0.225 m = 90 d1v = lambda t,v: g - (cd/m)*(v**2) t0 = 0 v0 = 0 h = 2 y0 = 1000 muestras = 11 # PROCEDIMIENTO velocidad = rungekutta2(d1v,t0,v0,h,muestras) ti = velocidad[:,0] vi = velocidad[:,1] # Altura, velocidad es contraria altura, # integrar en cada tramo por trapecios o Cuadratura de Gauss altura = integratrapecio_fi_tabla(ti,-vi,y0) # Tabla de resultados de tiempo, velocidad, altura altura = np.transpose([altura]) tabla = np.concatenate((velocidad[:,0:2],altura), axis = 1) # SALIDA np.set_printoptions(precision=4) print('velocidad con Runge-Kutta primera derivada') print(' [tiempo, velocidad, K1,K2]') print(velocidad) np.set_printoptions(precision=2) print('velocidad con RK2 y altura con trapecio') print(' [tiempo, velocidad, altura]') print(tabla)
Plantear con: [ Runge-Kutta para f''(x) ] [ Runge-Kutta para f'(x) ]
