s2Eva_IT2018_T2 Deducir Simpson 1/3

Ejercicio: 2Eva_IT2018_T2 Deducir Simpson 1/3

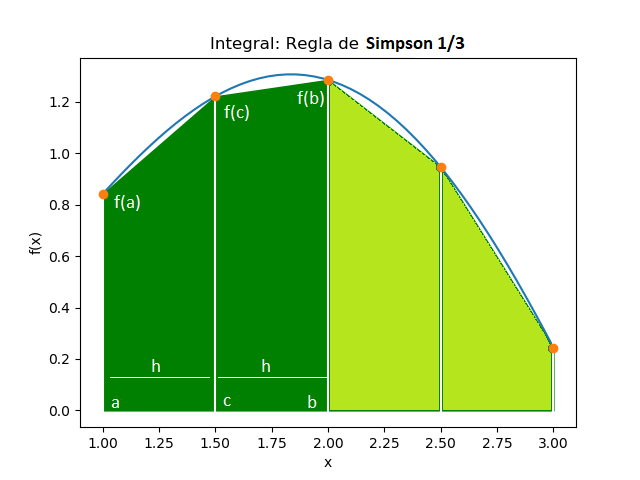
Para el problema, se usan los puntos: [a,f(a)], [b,f(b)] y [c,f(c)]
por donde pasa la curva f(x) aproximada a un polinomio de grado 2, $f(x) \approx p(x)$

\int_a^b f(x) dx \approx \int_a^b p(x) dx

p(x) = L_a f(a) + L_c f(c) + L_b f(b)

\int_a^b p(x) dx = \int_a^b \Big[ L_a f(a) +L_c f(c) + L_b f(b) \Big] dx =

= \int_a^b L_a f(a) dx + \int_a^b L_c f(c) dx + \int_a^b L_b f(b) dx

\int_a^b p(x) dx = I_1 + I_2 + I_3

Como referencia se usa la gráfica para relacionar a, b, c y h:

Primer Integral

Para el primer integral $I_1= \int_a^b L_a f(a) dx$ se tiene que:

L_a = \frac{(x-b)(x-c)}{(a-b)(a-c)} = \frac{(x-b)(x-c)}{(-2h)(-h)}

L_a = \frac{(x-b)(x-c)}{2h^2}

se convierte en:

I_1 = \int_a^b \frac{(x-b)(x-c)}{2h^2} f(a) dx = \frac{f(a)}{2h^2} \int_a^b (x-b)(x-c)dx

Para dejar la parte del integral en función de h, a y b, teniendo que c está en la mitad de [a,b], es decir c = (a+b)/2 , se usa:

u = x-a

por lo que $\frac{du}{dx}=1$ y $du = dx$

x-c = (u+a) - \frac{a+b}{2}

= u+ \frac{a-b}{2} = u - \frac{b-a}{2}

x-c = u-h

x-b = (u+a)-b = u-2\Big(\frac{b-a}{2}\Big) = u-2h

Se actualiza el integral de x entre [a,b] usando u = x-a, que se convierte el rango para u en [0, b-a] que es lo mismo que [0,2h]

\int_a^b (x-b)(x-c)dx = \int_0^{2h} (u-2h)(u-h)du =

= \int_0^{2h} \Big( u^2 - 2hu - uh + 2h^2 \Big) du

= \int_0^{2h} \Big( u^2 - 3hu + 2h^2 \Big) du

= \frac{u^3}{3}- 3h\frac{u^2}{2}+ 2h^2u \Big|_0^{2h}

= \frac{(2h)^3}{3}- 3h\frac{(2h)^2}{2} + 2h^2(2h) -(0-0+0)

= \frac{8h^3}{3}- 6h^3 + 4h^3 =\frac{8h^3}{3}- 2h^3

= \frac{2h^3}{3}

resultado que se usa en I₁

I_1= \frac{f(a)}{2h^2}\frac{2h^3}{3} =\frac{h}{3} f(a)

que es el primer término de la fórmula general de Simpson 1/3

Segundo Integral

Para el Segundo integral $I_2= \int_a^b L_c f(c) dx$ se tiene que:

L_c = \frac{(x-a)(x-b)}{(c-a)(c-b)} = \frac{(x-a)(x-b)}{(h)(-h)}

L_c = \frac{(x-a)(x-b)}{-h^2}

se convierte en:

I_2 = \frac{f(c)}{-h^2} \int_a^b (x-a)(x-b) dx

= \frac{f(c)}{-h^2} \int_0^{2h} (u)(u-2h) du

siendo:

\int_0^{2h}(u^2-2hu)du=\Big(\frac{u^3}{3}-2h\frac{u^2}{2}\Big)\Big|_0^{2h}

=\frac{(2h)^3}{3}-h(2h)^2-(0-0)

=\frac{8h^3}{3}-4h^3 = -\frac{4h^3}{3}

usando en I₂

I_2 = \frac{f(c)}{-h^2}\Big(-\frac{4h^3}{3}) = \frac{h}{3}4f(c)

Tarea: Continuar las operaciones para y tercer integral para llegar a la fórmula general de Simpson 1/3:

I = \frac{h}{3} \Big( f(a)+4f(c) + f(b) \Big)