Ejercicio: 2Eva_IT2018_T3 EDP Eliptica
Generar las ecuaciones a resolver usando diferencias finitas divididas centradas:
\frac{\partial ^2 u}{\partial x^2} + \frac{\partial ^2 u}{\partial y^2} = 2(x^2+y^2)por facilidad se sustituye también en la forma discreta de la ecuación:
f[i,j] = f(x_i,y_j) = 2(x_{i} ^2+y_{j} ^2)\frac{u[i-1,j]-2u[i,j]+u[i+1,j]}{\Delta x^2} + + \frac{u[i,j-1]-2u[i,j]+u[i,j+1]}{\Delta y^2} = f[i,j]
\frac{\Delta y^2}{\Delta x^2}\Big(u[i-1,j]-2u[i,j]+u[i+1,j]\Big) + + u[i,j-1]-2u[i,j]+u[i,j+1] = \Delta y^2 f[i,j]
dado que hx = hy = 1/3
\frac{\Delta y^2}{\Delta x^2} = 1(u[i-1,j]-2u[i,j]+u[i+1,j]) + + u[i,j-1]-2u[i,j]+u[i,j+1] = = \Delta y^2 f[i,j]
u[i-1,j]-4u[i,j]+u[i+1,j] + + u[i,j-1]+u[i,j+1] = \Delta y^2 f[i,j]
4u[i,j] = u[i-1,j]+u[i+1,j] + + u[i,j-1]+u[i,j+1]-\Delta y^2 f[i,j]
u[i,j] = \frac{1}{4} \Big(u[i-1,j]+u[i+1,j] + + u[i,j-1]+u[i,j+1]-\Delta y^2 f[i,j] \Big)
La última ecuación puede ser usada de forma iterativa, para lo cual hay que definir los valores iniciales de la matriz u.
Al conocer el rango de operación para los ejes x, y, hx, hy se realizan los cálculos para:
1. Evaluar los valores para cada eje x[i], y[j]
x[i]: [ 0. 0.33 0.67 1. ] y[j]: [ 0. 0.33 0.67 1. ]
2. Evaluar en cada punto generando una matriz f(i,j):
f[i,j]: [[ 0. 0.22 0.89 2. ] [ 0.22 0.44 1.11 2.22] [ 0.89 1.11 1.78 2.89] [ 2. 2.22 2.89 4. ]]
3. Se evaluan las funciones indicadas para la frontera y se tiene la matriz inicial para u:
matriz inicial u[i,j]: [[ 1. 1.33 1.67 2. ] [ 1.33 0. 0. 2.44] [ 1.67 0. 0. 3.11] [ 2. 2.44 3.11 4. ]]
con lo que se puede trabajar cada punto i,j de forma iterativa, teniendo como resultado para la matriz u:
resultado para u, iterando: converge = 1 [[ 1. 1.33 1.67 2. ] [ 1.33 1.68 2.05 2.44] [ 1.67 2.05 2.53 3.11] [ 2. 2.44 3.11 4. ]]
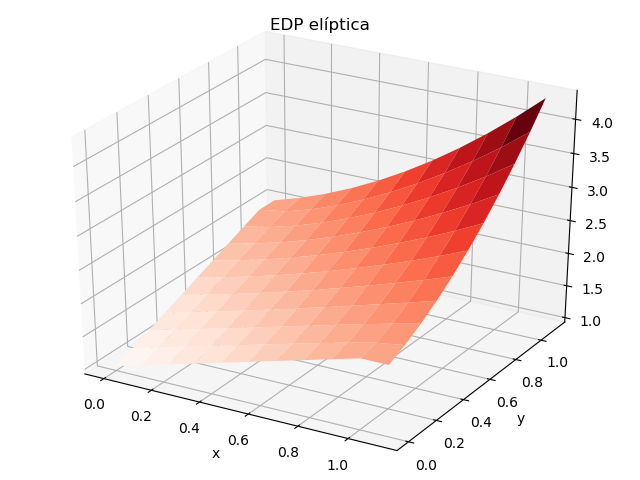
La gráfica usando una mayor resolución para tener una idea de la solución:
Los resultados se obtienen usando las siguientes instrucciones:
# 2da Evaluación I Término 2018 # Tema 3. EDP Eliptica import numpy as np # INGRESO # ejes x,y x0 = 0 ; xn = 1 ; hx = (1/3)# (1/3)/10 y0 = 0 ; yn = 1 ; hy = (1/3) # (1/3)/10 # Fronteras fux0 = lambda x: x+1 fu0y = lambda y: y+1 fux1 = lambda x: x**2 + x + 2 fu1y = lambda y: y**2 + y + 2 fxy = lambda x,y: 2*(x**2+y**2) # PROCEDIMIENTO xi = np.arange(x0,xn+hx,hx) yj = np.arange(y0,yn+hy,hy) n = len(xi) m = len(yj) # funcion f[xi,yi] fij = np.zeros(shape=(n,m), dtype = float) for i in range(0,n,1): for j in range(0,m,1): fij[i,j]=fxy(xi[i],yj[j]) # matriz inicial u[i,j] u = np.zeros(shape=(n,m), dtype = float) u[:,0] = fux0(xi) u[0,:] = fu0y(yj) u[:,m-1] = fux1(xi) u[n-1,:] = fu1y(yj) uinicial = u.copy() # Calcular de forma iterativa maxitera = 100 tolera = 0.0001 # valor inicial de iteración promedio = (np.max(u)+np.min(u))/2 u[1:n-1,1:m-1] = promedio # iterar puntos interiores itera = 0 converge = 0 erroru = 2*tolera # para calcular al menos una matriz while not(erroru=maxitera): itera = itera +1 nueva = np.copy(u) for i in range(1,n-1): for j in range(1,m-1): u[i,j] = (u[i-1,j]+u[i+1,j]+u[i,j-1]+u[i,j+1]-(hy**2)*fij[i,j])/4 diferencia = nueva-u erroru = np.linalg.norm(np.abs(diferencia)) if (erroru<tolera): converge=1 # SALIDA np.set_printoptions(precision=2) print('x[i]:') print(xi) print('y[j]:') print(yj) print('f[i,j]:') print(fij) print('matriz inicial u[i,j]:') print(uinicial) print('resultado para u, iterando: ') print('converge = ', converge) print('iteraciones = ', itera) print(u)
para obtener la gráfica se debe añadir:
# Gráfica import matplotlib.pyplot as plt from matplotlib import cm from mpl_toolkits.mplot3d import Axes3D X, Y = np.meshgrid(xi, yj) figura = plt.figure() ax = Axes3D(figura) U = np.transpose(u) # ajuste de índices fila es x ax.plot_surface(X, Y, U, rstride=1, cstride=1, cmap=cm.Reds) plt.title('EDP elíptica') plt.xlabel('x') plt.ylabel('y') plt.show()