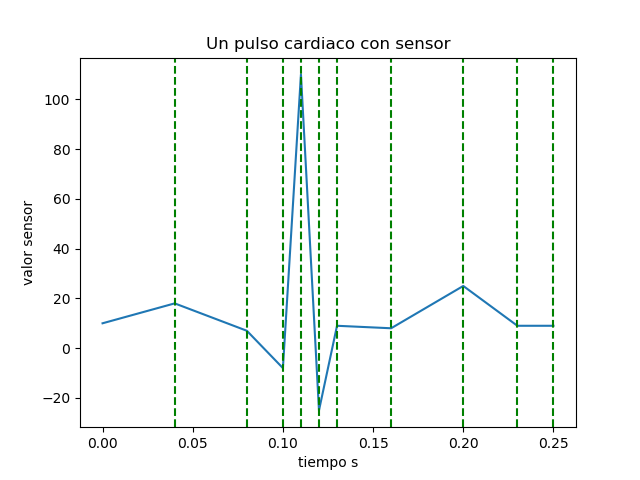
Ejercicio: 2Eva_IT2019_T1 Esfuerzo en pulso cardiaco
Para resolver el ejercicio, la función a integrar es el cuadrado de los valores. Para minimizar los errores se usarán TODOS los puntos muestreados, aplicando los métodos adecuados.
Con aproximación de Simpson se requiere que los tamaños de paso sean iguales en cada segmento.
Por lo que primero se revisa el tamaño de paso entre lecturas.
tamaño de paso h: [0.04 0.04 0.02 0.01 0.01 0.01 0.03 0.04 0.03 0.02 0. ] tiempos: [0. 0.04 0.08 0.1 0.11 0.12 0.13 0.16 0.2 0.23 0.25] ft: [ 10. 18. 7. -8. 110. -25. 9. 8. 25. 9. 9.]
Observando los tamaños de paso se tiene que:
– entre dos tamaños de paso iguales se usa Simpson de 1/3
– entre tres tamaños de paso iguales se usa Simpson de 3/8
– para tamaños de paso variables se usa trapecio.
Se procede a obtener el valor del integral,
Intervalo [0,0.8], h = 0.04
I_{S13} = \frac{0.04}{3}(10^2+4(18^2)+7^2)Intervalo [0.08,0.1], h = 0.02
I_{Tr1} = \frac{0.02}{2}(7^2+(-8)^2)Intervalo [0.1,0.13], h = 0.01
I_{S38} = \frac{3}{8}(0.01)((-8)^2+3(110)^2+3(-25)^2+9^2)Intervalo [0.13,0.25], h = variable
I_{Tr2} = \frac{0.03}{2}(9^2+8^2) I_{Tr3} = \frac{0.04}{2}(8^2+25^2) I_{Tr4} = \frac{0.03}{2}(25^2+9^2) I_{Tr5} = \frac{0.02}{2}(9^2+9^2)El integral es la suma de los valores parciales, y con el resultado se obtiene el valor Xrms requerido.
I_{total} = \frac{1}{0.08-0}I_{S13}+\frac{1}{0.1-0.08}I_{Tr1} +\frac{1}{0.13-0.1}I_{S38} + \frac{1}{0.16-0.13}I_{Tr2} + \frac{1}{0.2-0.16}I_{Tr3} +\frac{1}{0.23-0.2}I_{Tr4} + \frac{1}{0.25-0.23}I_{Tr5} X_{rms} = \sqrt{I_{total}}Los valores resultantes son:
Is13: 19.26666666666667 ITr1: 1.1300000000000001 Is38: 143.7 ITr2: 2.175 ITr3: 13.780000000000001 ITr4: 10.59 ITr5: 1.62 Itotal: 5938.333333333333 Xrms: 77.06058222809722
Tarea: literal b
Para Simpson 1/3
error_{trunca} = -\frac{h^5}{90} f^{(4)}(z)Para Simpson 3/8
error_{truncamiento} = -\frac{3}{80} h^5 f^{(4)} (z)Para trapecios
error_{truncar} = -\frac{h^3}{12}f''(z)Algoritmo en Python
# 3Eva_IT2019_T1 Esfuerzo Cardiaco import numpy as np import matplotlib.pyplot as plt # INGRESO t = np.array([0.0,0.04,0.08,0.1,0.11,0.12,0.13,0.16,0.20,0.23,0.25]) ft = np.array([10., 18, 7, -8, 110, -25, 9, 8, 25, 9, 9]) # PROCEDIMIENTO # Revisar tamaño de paso h n = len(t) dt = np.zeros(n, dtype=float) for i in range(0,n-1,1): dt[i]=t[i+1]-t[i] # Integrales Is13 = (0.04/3)*((10)**2 + 4*((18)**2) + (7)**2) ITr1 = (0.02/2)*((7)**2 + (-8)**2) Is38 = (3/8)*0.01*((-8)**2 + 3*((110)**2) + 3*((-25)**2) + (9)**2) ITr2 = (0.03/2)*((9)**2 + (8)**2) ITr3 = (0.04/2)*((8)**2 + (25)**2) ITr4 = (0.03/2)*((25)**2 + (9)**2) ITr5 = (0.02/2)*((9)**2 + (9)**2) Itotal = (1/(0.08-0.0))*Is13 + (1/(0.1-0.08))*ITr1 Itotal = Itotal + (1/(0.13-0.1))*Is38 + (1/(0.16-0.13))*ITr2 Itotal = Itotal + (1/(0.20-0.16))*ITr3 + (1/(0.23-0.20))*ITr4 Itotal = Itotal + (1/(0.25-0.23))*ITr5 Xrms = np.sqrt(Itotal) # SALIDA print('tamaño de paso h:') print(dt) print('tiempos:') print(t) print('ft: ') print(ft) print('Is13: ', Is13) print('ITr1: ', ITr1) print('Is38: ', Is38) print('ITr2: ', ITr2) print('ITr3: ', ITr3) print('ITr4: ', ITr4) print('ITr5: ', ITr5) print('Itotal: ', Itotal) print('Xrms: ', Xrms) # Grafica plt.plot(t,ft) for i in range(1,n,1): plt.axvline(t[i], color='green', linestyle='dashed') plt.xlabel('tiempo s') plt.ylabel('valor sensor') plt.title('Un pulso cardiaco con sensor') plt.show()