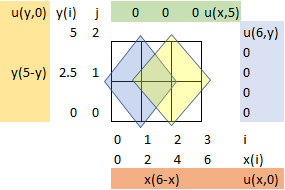
Ejercicio: 2Eva_IT2019_T3 EDP Elíptica Placa 6×5
La ecuación se discretiza con diferencias divididas centradas
\frac{\partial^2 u}{\partial x^2} (x,y)+\frac{\partial ^2 u}{\partial y^2 } (x,y) = -\frac{q}{K} \frac{u_{i+1,j}-2u_{i,j}+u_{i-1,j}}{(\Delta x)^2} + \frac{u_{i,j+1}-2u_{i,j}+u_{i,j-1}}{(\Delta y)^2}= -\frac{q}{K}Para procesar los datos se toma como referencia la malla
se agrupan los términos conocidos de las diferencias divididas
\frac{(\Delta y)^2}{(\Delta x)^2} \Big( u_{i+1,j}-2u_{i,j} +u_{i-1,j} \Big) + u_{i,j+1}-2u_{i,j}+u_{i,j-1}=-\frac{q}{K}(\Delta y)^2Considerando que hx =2, hy= 2.5 son diferentes, se mantiene el valor de λ para el desarrollo.
\lambda = \frac{(\Delta y)^2}{(\Delta x)^2} = \frac{(2.5)^2}{(2)^2} = 1.5625 \lambda u_{i+1,j}-2\lambda u_{i,j} +\lambda u_{i-1,j} + u_{i,j+1}-2u_{i,j}+u_{i,j-1}=-\frac{q}{K}(\Delta y)^2Se agrupan términos de u que son iguales
\lambda u_{i+1,j}-2(1+\lambda) u_{i,j} +\lambda u_{i-1,j} + u_{i,j+1}+u_{i,j-1}=-\frac{q}{K}(\Delta y)^2con lo que se puede generar el sistema de ecuaciones a resolver para los nodos de la malla.
i = 1 , j=1
1.5625 u_{2,1}-2(1+ 1.5625) u_{1,1} + 1.5625 u_{0,1} + +u_{1,2}+u_{1,0}=-\frac{1.5}{1.04}(2.5)^2 1.5625 u_{2,1}-5.125u_{1,1} + 1.5625 y_1(5-y_1) + + 0+x_i(6-x_i)=-9.0144 1.5625 u_{2,1}-5.125u_{1,1} + 1.5625[ 1(5-1)]+ + 0+2(6-2)=-9.0144 1.5625 u_{2,1}-5.125 u_{1,1} = =-9.0144 - 1.5625 [1(5-1)] - 0-2(6-2)1.5625 u_{2,1}-5.125 u_{1,1} =-23.2644
i=2, j=1
1.5625 u_{3,1}-2(1+1.5625) u_{2,1} +1.5625 u_{1,1} + +u_{2,2}+u_{2,0}=-9.0144 1.5625 (0)-5.125 u_{2,1} +1.5625 u_{1,1} + 0 +x_2(6-x_2)=-9.0144 -5.125 u_{2,1} +1.5625 u_{1,1} + 0 +4(6-4)=-9.0144-5.125 u_{2,1} +1.5625 u_{1,1} =-17.0144
las ecuaciones a resolver son:
1.5625 u_{2,1}-5.125 u_{1,1} =-23.2644 -5.125 u_{2,1} +1.5625 u_{1,1} =-17.0144cuya solución es:
u_{2,1} = 5.1858 u_{1,1} =6.1204Resuelto usando:
import numpy as np A = np.array([[1.5625,-5.125], [-5.125, 1.5625]]) B = np.array([-23.2644,-17.0144]) x = np.linalg.solve(A,B) print(x)