s3Eva_2023PAOII_T1 Intersección con círculo

Ejercicio: 3Eva_2023PAOII_T1 Intersección con círculo
Encuentre las raíces de las ecuaciones simultaneas siguientes:

literal a y b

Use el enfoque gráfico para obtener los valores iniciales.

$2y+1.75 x = 35.25$ $(y-7.6)^2 + (x-8.6)^2 = (6.7)^2$

se despeja la variable dependiente de cada ecuación, para la primera:

$f(x) = y = \frac{35.25}{2} - \frac{1.75}{2} x$

para la segunda:

$(y-7.6)^2 = (6.7)^2 - (x-8.6)^2$ $g(x) = y = \sqrt{(6.7)^2 - (x-8.6)^2} + 7.6$

Al buscar la intersección entre f(x) y g(x) se puede encontrar con la raiz de:

$distancia(x) = f(x) - g(x)$ $distancia(x) = \Big( \frac{35.25}{2} - \frac{1.75}{2} x\Big) - \Big(\sqrt{(6.7)^2 - (x-8.6)^2} + 7.6\Big)$

La primera ecuación es una recta, por lo que no aporta a las cotas de la gráfica.

La segunda ecuación es la general de un círculo centrado en (7.6, 8.6) y radio 6.7, por lo que se considera el intervalo para la gráfica entre:

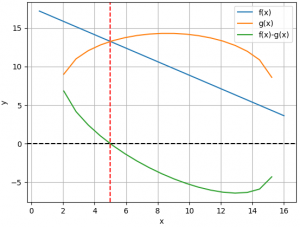
$[7.6 -6.7, 7.6+6.7]$ $[0.9, 14.3]$

Con lo que se puede formar la gráfica de la parte superior del círculo en Python:

Instrucciones en Python

# 3Eva_2023PAOII_T1 Intersección con círculo
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
f = lambda x: -(1.75/2)*x + (35.25/2)
g = lambda x: np.sqrt(6.7**2-(x-8.6)**2) + 7.6
distancia = lambda x: f(x)- g(x)

a = 0.5
b = 16
muestras = 21

# PROCEDIMIENTO
# literal a y b
xi = np.linspace(a,b,muestras)
fi = f(xi)
gi = g(xi)
dist_i = distancia(xi)

# SALIDA - Grafica
# literal a y b
plt.plot(xi,fi, label='f(x)')
plt.plot(xi,gi, label='g(x)')
plt.plot(xi,dist_i, label='f(x)-g(x)')
plt.axhline(0, color='black', linestyle='dashed')
plt.axvline(5, color='red', linestyle='dashed')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid()
plt.show()

literal c

Un punto inicial de búsqueda dentro del intervalo puede ser x0=3.

Para Newton-Raphson se usa:

$f(x) = \Big( \frac{35.25}{2} - \frac{1.75}{2} x\Big) - \Big(\sqrt{(6.7)^2 - (x-8.6)^2} + 7.6\Big)$ $\frac{d}{dx}f(x) = -\frac{8.6(0.1162-0.0135x)}{\sqrt{0.0609-(0.1162x-1)^2}}-0.875$

(derivada obtenida con sympy)

itera = 0 ; xi = 3

$f(3) = \Big( \frac{35.25}{2} - \frac{1.75}{2} (3)\Big) - \Big(\sqrt{(6.7)^2 - ((3)-8.6)^2} + 7.6\Big)$ $\frac{d}{dx}f(3) = -\frac{8.6(0.1162-0.0135(3))}{\sqrt{0.0609-(0.1162(3)-1)^2}}-0.875$ $x_1 = x_0 - \frac{f(3)}{\frac{d}{dx}f(3)} = 4.55$ $tramo = |4.55-3| = 1.55$

itera = 1 ; xi = 4.55

$f(3) = \Big( \frac{35.25}{2} - \frac{1.75}{2} (4.55)\Big) - \Big(\sqrt{(6.7)^2 - ((4.55)-8.6)^2} + 7.6\Big)$ $\frac{d}{dx}f(3) = -\frac{8.6(0.1162-0.0135(4.55))}{\sqrt{0.0609-(0.1162(4.55)-1)^2}}-0.875$ $x_2 = x_1 - \frac{f(4.55)}{\frac{d}{dx}f(4.55)} = 4.98$ $tramo = |4.98-4.55| = 0.43$

itera = 2 ; xi = 4.98

$f(3) = \Big( \frac{35.25}{2} - \frac{1.75}{2} (4.98)\Big) - \Big(\sqrt{(6.7)^2 - ((4.98)-8.6)^2} + 7.6\Big)$ $\frac{d}{dx}f(3) = -\frac{8.6(0.1162-0.0135(4.98))}{\sqrt{0.0609-(0.1162(4.98)-1)^2}}-0.875$ $x_3 = x_2 - \frac{f(4.98)}{\frac{d}{dx}f(4.98)} = 4.99$ $tramo = |4.99-4.98| = 0.01$

literal d

El error disminuye en cada iteración, por lo que el método converge.

Con el algoritmo se muestra que converge a x=5

dfg(x) = 
     8.6*(0.116279069767442 - 0.0135208220659816*x)          
- --------------------------------------------------- - 0.875
     ________________________________________________        
    /                                              2         
  \/  0.606949702541915 - (0.116279069767442*x - 1)          

['xi', 'xnuevo', 'tramo']
[[3.0000e+00 4.5524e+00 1.5524e+00]
 [4.5524e+00 4.9825e+00 4.3018e-01]
 [4.9825e+00 4.9995e+00 1.6999e-02]
 [4.9995e+00 4.9996e+00 2.3865e-05]]
raiz en:  4.9995611025201585
con error de:  2.3865455016647275e-05

Instrucciones en Python

# 3Eva_2023PAOII_T1 Intersección con círculo
import sympy as sym
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
# forma algebraica con sympy
x = sym.Symbol('x')
f = -(1.75/2)*x + (35.25/2)
g = sym.sqrt(6.7**2-(x-8.6)**2) + 7.6
distancia = f - g

x0 = 3
tolera = 0.0001 # 1e-4

# PROCEDIMIENTO
# literal c
dfg = sym.diff(distancia,x)
# convierte a forma numerica con numpy
# Newton-Raphson
fx = sym.lambdify(x,distancia)
dfx = sym.lambdify(x,dfg)

tabla = []
tramo = abs(2*tolera)
xi = x0
while (tramo>=tolera):
    xnuevo = xi - fx(xi)/dfx(xi)
    tramo  = abs(xnuevo-xi)
    tabla.append([xi,xnuevo,tramo])
    xi = xnuevo

# convierte la lista a un arreglo.
tabla = np.array(tabla)
n = len(tabla)

# SALIDA
print('dfg(x) = ')
sym.pprint(dfg)
print()
print(['xi', 'xnuevo', 'tramo'])
np.set_printoptions(precision = 4)
print(tabla)
print('raiz en: ', xi)
print('con error de: ',tramo)