Ejercicio: 3Eva_2023PAOII_T2 perfil de un peón
literal a y b
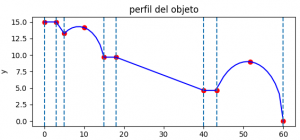Para el planteamiento de los polinomios, es necesario observar la gráfica proporcionada para el ejercicio y la correspondiente tabla de datos:
| xi | 0 | 3 | 5 | 9.985 | 14.97 | 17.97 | 40.04 | 43.29 | 51.6456 | 60 |
| yi | 15 | 15 | 13.25 | 14.155 | 9.676 | 9.676 | 4.64 | 4.64 | 8.976 | 0 |
Para el intervalo [0,3], El perfil se describe con una constante, por lo tanto:
p_1(x) = 15Para el intervalo [3,5] el perfil se describe como una recta con pendiente negativa.
p_2(x) =a_0 + a_1 x a_1 = \frac{ 13.25-15}{5-3} = -0.875 p_2(5) = 13.25 =a_0 -0.875 (5) a_0 = 13.25 +0.875 (5) = 17.625 p_2(x) = -0.875 x + 17.625Para el con los puntos xi = [5, 9.985, 14.97] el perfil se describe con tres puntos, por lo que el polinomio de interpolación puede ser de grado 2. Usando el método de Lagrange:
p_3(x) =\frac{(x-9.985)( x-14.97)}{(5-9.985)( 5-14.97)} 13.25 + +\frac{(x-5)( x-14.97)}{(9.985-5)( 9.985-14.97)} 14.155 + +\frac{(x-5)( x-9.985)}{(14.97-5)( 14.97-9.985)} 9.676 +simplificando la expresión con Python y Sympy:
P_3(x) = -0.1083 x^2 + 1.8047 x + 6.9341
literal c
El error para los polinomios acorde a la gráfica proporcionada es cero para los tramos [0,3] y [3,5], dado que el primero es una constante y el segundo es una recta con pendiente.
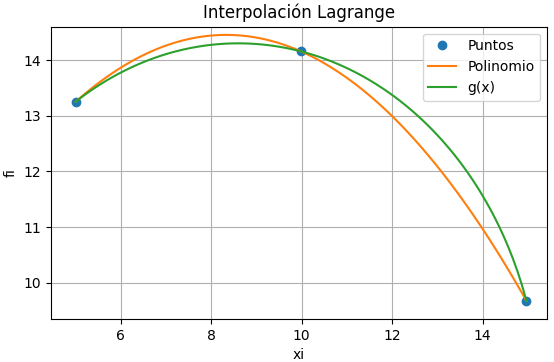
El error de mayor magnitud se presenta con la interpolación entre el círculo de la ecuación del tema 1 y el polinomio de grado 2 en el intervalo [5, 14.97]. Tomando como ejemplo el punto intermedio del tramo derecho en:
x_k = \frac{14.97-5}{4} + 9.985= 12.4775 p_3(12.4775) = -0.1083(12.4775)^2 + 1.8047(12.4775) + 6.9341 = 12.5889 f(12.4775) = \sqrt{6.7^2-(12.4775-8.6)^2} + 7.6 = 13.0639 errado = |p_3(12.4775) - f(12.4775)| = 0.4750literal d
Se puede mejorar la aproximación del polinomio aumentando el grado y número de puntos a usar dentro del intervalo. El resultado se debería acercar mas al perfil superior del círculo de referencia del tema 1.
Resultados para el intervalo [5, 14.97]
valores de fi: [13.25 14.1552 9.6768] divisores en L(i): [ 49.70045 -24.850225 49.70045 ] Polinomio de Lagrange, expresiones 0.266597183727713*(x - 14.97)*(x - 9.985) - 0.569620596996607*(x - 14.97)*(x - 5.0) + 0.194702462452553*(x - 9.985)*(x - 5.0) Polinomio de Lagrange: -0.108320950816341*x**2 + 1.80477420224566*x + 6.93415275918024
Instrucciones Python
# 3Eva_2023PAOII_T2 perfil de un peón import sympy as sym import numpy as np import matplotlib.pyplot as plt # INGRESO xj=[ 0, 3, 5. , 9.985 , 14.97 , 17.97, 40.04, 43.29, 51.6449, 60] yj=[15,15,13.25,14.1552, 9.6768, 9.67, 4.64, 4.64, 8.9768, 0.] # Datos de prueba ia = 2 ib = 4+1 xi = np.array(xj[ia:ib]) fi = np.array(yj[ia:ib]) g = lambda x: np.sqrt(6.7**2-(x-8.6)**2) + 7.6 muestras = 21 # PROCEDIMIENTO # Polinomio de Lagrange n = len(xi) x = sym.Symbol('x') polinomio = 0 divisorL = np.zeros(n, dtype = float) for i in range(0,n,1): # Termino de Lagrange numerador = 1 denominador = 1 for j in range(0,n,1): if (j!=i): numerador = numerador*(x-xi[j]) denominador = denominador*(xi[i]-xi[j]) terminoLi = numerador/denominador polinomio = polinomio + terminoLi*fi[i] divisorL[i] = denominador # simplifica el polinomio polisimple = polinomio.expand() # para evaluación numérica px = sym.lambdify(x,polisimple) # Puntos para la gráfica muestras = 101 a = np.min(xi) b = np.max(xi) pxi = np.linspace(a,b,muestras) pfi = px(pxi) gi = g(pxi) # SALIDA print(' valores de fi: ',fi) print('divisores en L(i): ',divisorL) print() print('Polinomio de Lagrange, expresiones') print(polinomio) print() print('Polinomio de Lagrange: ') print(polisimple) # Gráfica plt.plot(xi,fi,'o', label = 'Puntos') plt.plot(pxi,pfi, label = 'Polinomio') plt.plot(pxi,gi, label = 'g(x)') plt.legend() plt.xlabel('xi') plt.ylabel('fi') plt.title('Interpolación Lagrange') plt.grid() plt.show()