Publicado en por Edison Del Rosario

s3Eva_IIT2007_T1 EDP Eliptica, problema de frontera

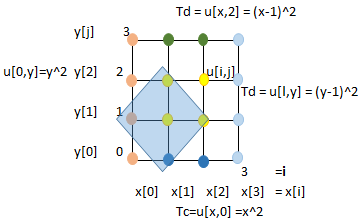
Ejercicio: 3Eva_IIT2007_T1 EDP Eliptica, problema de frontera

Con los datos del ejercicio se plantean de la siguiente forma en los bordes:

La ecuación a resolver es:

\frac{\delta^2u}{\delta x^2} +\frac{\delta^2 u}{\delta y^2} = 4

Que en su forma discreta, con diferencias divididas centradas es:

\frac{u[i-1,j]-2u[i,j]+u[i+1,j]}{(\Delta x)^2} + \frac{u[i,j-1]-2u[i,j]+u[i,j+1]}{(\Delta y)^2} = 4

Al agrupar constantes se convierte en:

u[i-1,j]-2u[i,j]+u[i+1,j] + + \frac{(\Delta x)^2}{(\Delta y)^2} \Big(u[i,j-1]-2u[i,j]+u[i,j+1] \Big)= 4(\Delta x)^2

Siendo Δx= 1/3 y Δy =2/3, se mantendrá la relación λ = (Δx/Δy)2

u[i-1,j]-2u[i,j]+u[i+1,j] + + \lambda u[i,j-1]-2\lambda u[i,j]+\lambda u[i,j+1] = = 4(\Delta x)^2
u[i-1,j]-2(1+\lambda)u[i,j]+u[i+1,j] + + \lambda u[i,j-1]+\lambda u[i,j+1] = 4(\Delta x)^2

Se pueden realizar las iteraciones para los nodos y reemplaza los valores de frontera:

i=1 y j=1

u[0,1]-2(1+\lambda)u[1,1]+u[2,1] + + \lambda u[1,0]+\lambda u[1,2] = 4(\Delta x)^2 \Delta y^2-2(1+\lambda)u[1,1]+u[2,1] + + \Delta x^2+\lambda u[1,2] = 4(\Delta x)^2 -2(1+\lambda)u[1,1]+u[2,1] +\lambda u[1,2] = 4(\Delta x)^2 - \Delta y^2 - \Delta x^2 -2(1+0.25)u[1,1]+u[2,1] +0.25 u[1,2] = 4(1/3)^2 - (2/3)^2- (1/3)^2 -2.5u[1,1]+u[2,1] +0.25 u[1,2] = -0.1111

i=2 , j=1

u[1,1]-2(1+\lambda)u[2,1]+u[3,1] + + \lambda u[2,0]+\lambda u[2,2] = 4(\Delta x)^2 u[1,1]-2(1+\lambda)u[2,1]+(\delta y-1)^2 + + \Delta x^2 +\lambda u[2,2] = 4(\Delta x)^2 u[1,1]-2(1+\lambda)u[2,1] + \lambda u[2,2] = 4(\Delta x)^2 - (\Delta y-1)^2 - \Delta x^2 u[1,1]-2(1+0.25)u[2,1] + 0.25 u[2,2] = 4(1/3)^2 - (2/3-1)^2 - (1/3)^2 u[1,1]-2.5u[2,1] + 0.25 u[2,2] = 0.2222

i=1 , j=2

u[0,2]-2(1+\lambda)u[1,2]+u[2,2] + + \lambda u[1,1]+\lambda u[1,3] = 4(\Delta x)^2 (2\Delta y^2)-2(1+\lambda)u[1,2]+u[2,2] + + \lambda u[1,1]+\lambda (\Delta x-1)^2 = 4(\Delta x)^2 -2(1+\lambda)u[1,2]+u[2,2] + \lambda u[1,1] = 4(\Delta x)^2 - (2\Delta y^2) -\lambda (\Delta x-1)^2 -2(1+0.25)u[1,2]+u[2,2] + 0.25 u[1,1] = 4(1/3)^2 - (2(2/3)^2] -0.25 (1/3-1)^2 -2.5u[1,2]+u[2,2] + 0.25 u[1,1] = -0.5555

i=2, j=2

u[1,2]-2(1+\lambda)u[2,2]+u[3,2] + + \lambda u[2,1]+\lambda u[2,3] = 4(\Delta x)^2 u[1,2]-2(1+\lambda)u[2,2]+(\Delta y-1)^2 + + \lambda u[2,1]+\lambda (\Delta x-1)^2 = 4(\Delta x)^2 u[1,2]-2(1+\lambda)u[2,2] + \lambda u[2,1] =4(\Delta x)^2- (\Delta y-1)^2 -\lambda (\Delta x-1)^2 u[1,2]-2(1+0.25)u[2,2] + 0.25 u[2,1] =4(1/3)^2- (2/3-1)^2 -0.25(1/3-1)^2 u[1,2]-2.5u[2,2] + 0.25 u[2,1] =-0.2222

Obtiene el sistema de ecuaciones a resolver:

-2.5u[1,1]+u[2,1] +0.25 u[1,2] = -0.1111 u[1,1]-2.5u[2,1] + 0.25 u[2,2] = 0.2222 -2.5u[1,2]+u[2,2] + 0.25 u[1,1] = -0.5555 u[1,2]-2.5u[2,2] + 0.25 u[2,1] =-0.2222

Se escribe en forma matricial Ax=B

\begin {bmatrix} -2.5 && 1&&0.25&&0 \\1&&-2.5&&0&&0.25\\0.25&&0&&-2.5&&1\\0&&0.25&&1&&-2.5\end{bmatrix} \begin {bmatrix} u[1,1] \\ u[2,1]\\ u[1,2]\\u[2,2] \end{bmatrix} = \begin {bmatrix}-0.1111\\0.2222\\-0.5555\\-0.2222 \end{bmatrix}

que se resuelve con un algoritmo:

import numpy as np

A = np.array([[-2.5,1,0.25,0],
              [1,-2.5,0,0.25],
              [0.25,0,-2.5,1],
              [0,0.25,1,-2.5]])
B = np.array([-0.1111,0.2222,-0.5555,-0.2222])

x = np.linalg.solve(A,B)

print(x)

y los resultados son:

[ 0.05762549 -0.04492835  0.31156835  0.20901451]