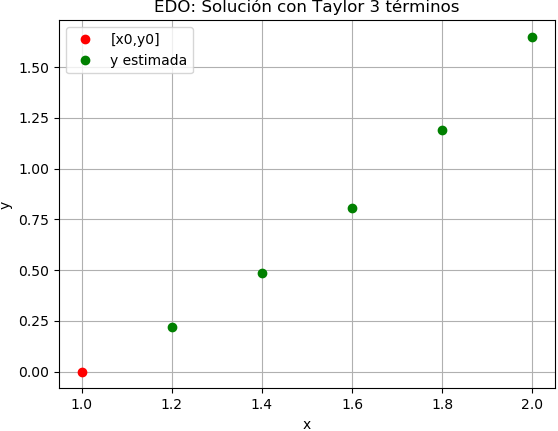
Ejercicio: 3Eva_IIT2007_T3 EDO Taylor orden 2
La ecuación del problema es:
y'= 1 +\frac{y}{t} + \Big(\frac{y}{t}\Big) ^2 1\leq t\leq 2 y(1)=0, h=0.2Tomando como referencia Taylor de 3 términos más el término de error O(h3)
y_{i+1} = y_i +\frac{h}{1!}y'_i + \frac{h^2}{2!}y''_i + \frac{h^3}{3!}y'''_iSe usa hasta el tercer término para el algoritmo.
y_{i+1} = y_i +\frac{h}{1!}y'_i + \frac{h^2}{2!}y''_iSe determina que se requiere la segunda derivada para completar la aproximación. A partir de la ecuación del problema se aplica en cada término:
\Big(\frac{u}{v}\Big)' = \frac{u'v-uv' }{v^2} y'= 1 +\frac{y}{t} + \frac{y^2}{t^2} y''= 0+\frac{y't-y}{t^2} + \frac{2yy't^2-2y^2t}{t^4} y''= \frac{y't-y}{t^2} + \frac{2y\Big(1 +\frac{y}{t} + \frac{y^2}{t^2}\Big) t^2-2y^2t}{t^4}Con lo que se realizan las iteraciones para llenar la tabla
iteración 1
t0 = 1
y0= 0
y'= 1 +\frac{0}{1} + \Big(\frac{0}{1}\Big)^2 = 1 y''= \frac{(1)(1)-0}{(1)^2} + \frac{2(0)(1)(1)^2-2(0)^2(1)}{(1)^4} = 1 y_{1} = 0 +\frac{0.2}{1!}(1) + \frac{0.2^2}{2!}(1) = 0.22t1 = t0 + h = 1 + 0.2 = 1.2
iteración 2
t1 = 1.2
y1= 0.22
y'= 1 +\frac{0.22}{1.2} + \Big(\frac{0.22}{1.2}\Big) ^2 = 1.21694444 y''= \frac{y'(1.2)-0.22}{1.2^2} + \frac{2(0.22)y'(1.2)^2-2(0.22)^2(1.2)}{(1.2)^4} = 1.17716821 y_{2} = 0.22 +\frac{0.2}{1!}(1.21694444) + \frac{0.2^2}{2!}(1.17716821) = 0.48693225t2 = t1 + h = 1.2 + 0.2 = 1.4
iteración 3
t2 = 1.4
y2= 0.48693225
y'= 1 +\frac{0.48693225}{1.4} + \Big(\frac{0.48693225}{1.4}\Big) ^2 = 1.46877968 y''= \frac{(1.46877968)(1.4)-0.48693225}{1.4^2} + \frac{2(0.48693225)(1.46877968)(1.4)^2-2(0.48693225)^2(1.4)}{1.4^4} = 1.35766995 y_{3} = 0.48693225 +\frac{0.2}{1!}(1.46877968) + \frac{0.2^2}{2!}(1.35766995) = 0.80784159t3 = t2 + h = 1.4 + 0.2 = 1.6
Con lo que se puede realizar el algoritmo, obteniendo la siguiente tabla:
estimado [xi, yi, d1yi, d2yi] [[1. 0. 1. 1. ] [1.2 0.22 1.21694444 1.17716821] [1.4 0.48693225 1.46877968 1.35766995] [1.6 0.80784159 1.759826 1.57634424] [1.8 1.19133367 2.09990017 1.8564435 ] [2. 1.64844258 0. 0. ]]