Ejercicio: 3Eva_IIT2019_T1 Lanzamiento de Cohete
A partir de la tabla del enunciado se realiza la tabla de diferencias finitas.
| i | ti | fi | Δfi | Δ2fi | Δ3fi | Δ4fi | Δ5fi |
| 1 | 0 | 0 | 32 | -6 | 0 | 0 | 0 |
| 2 | 25 | 32 | 26 | -6 | 0 | 0 | |
| 3 | 50 | 58 | 20 | -6 | 0 | ||
| 4 | 75 | 78 | 14 | -6 | |||
| 5 | 100 | 92 | 8 | ||||
| 6 | 125 | 100 |
Observando que a partir de la tercera diferencia finita los valores son cero, por lo que se usa la fórmula general de diferencias finitas divididas hasta el polinomio de grado 2.
p_2 (x) = f_0 + \frac{\Delta f_0}{h} (x - x_0) + + \frac{\Delta^2 f_0}{2!h^2} (x - x_0)(x - x_1)al sustituir los valores conocidos, se convierte en,
p_2 (t) =0 + \frac{32}{25} (t -0) + + \frac{-6}{2(25)^2} (t -0)(t - 25) =\frac{32}{25}t + \frac{-3}{(25)^2} (t^2 - 25t) =\frac{32}{25}t + \frac{-3}{(25)^2} t^2 - \frac{-3}{(25)^2}25t =\frac{7}{5}t - \frac{3}{625} t^2 y(t) =p_2 (t) =1.4 t - 0.0048 t^2Con lo que se puede obtener la velocidad:
y'(t) = 1.4 - 0.0096 ty luego la aceleración:
y''(t) = - 0.0096Si el error es el próximo término del polinomio Δ3fi entonces se estima en cero.
Tarea: Evaluar la velocidad y aceleración para cada punto de la tabla
La gráfica del polinomio encontrado es: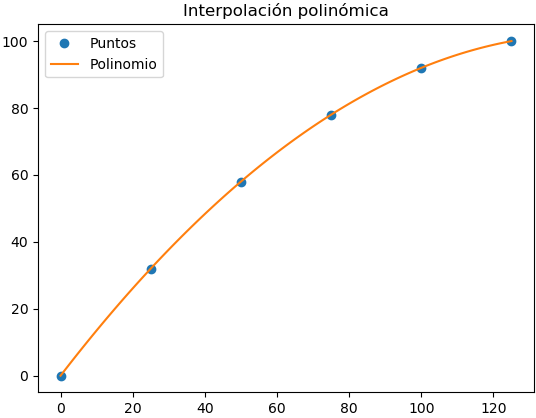
Algoritmo en Python
El algoritmo realizado en Python entrega los siguientes resultados:
[[ i, ti, fi, df1, df2, df3, df4, df5, df6]] [[ 1. 0. 0. 32. -6. 0. 0. 0. 0.] [ 2. 25. 32. 26. -6. 0. 0. 0. 0.] [ 3. 50. 58. 20. -6. 0. 0. 0. 0.] [ 4. 75. 78. 14. -6. 0. 0. 0. 0.] [ 5. 100. 92. 8. 0. 0. 0. 0. 0.] [ 6. 125. 100. 0. 0. 0. 0. 0. 0.]] polinomio: -0.0048*t**2 + 1.4*t
las instrucciones en Python son:
# 3Eva_IIT2019_T1 Lanzamiento de Cohete # Tarea: Verificar tamaño de vectores # considerar puntos no equidistantes en eje t import numpy as np import matplotlib.pyplot as plt import sympy as sym # INGRESO , Datos de prueba ti = np.array([0.0, 25, 50, 75, 100, 125]) fi = np.array([0.0, 32, 58, 78, 92, 100]) # PROCEDIMIENTO # Tabla de diferencias finitas titulo = ['i','ti','fi'] n = len(ti) # cambia a forma de columnas i = np.arange(1,n+1,1) i = np.transpose([i]) ti = np.transpose([ti]) fi = np.transpose([fi]) # Añade matriz de diferencias dfinita = np.zeros(shape=(n,n),dtype=float) tabla = np.concatenate((i,ti,fi,dfinita), axis=1) # Sobre matriz de diferencias, por columnas [n,m] = np.shape(tabla) c = 3 diagonal = n-1 while (c<m): # Aumenta el título para cada columna titulo.append('df'+str(c-2)) # calcula cada diferencia por fila f = 0 while (f < diagonal): tabla[f,c] = tabla[f+1,c-1]-tabla[f,c-1] f = f+1 diagonal = diagonal - 1 c = c+1 # POLINOMIO con diferencias finitas # caso: puntos en eje t equidistantes dfinita = tabla[:,3:] n = len(dfinita) t = sym.Symbol('t') h = ti[1,0]-ti[0,0] polinomio = fi[0,0] for c in range(1,n,1): denominador = np.math.factorial(c)*(h**c) factor = dfinita[0,c-1]/denominador termino=1 for f in range(0,c,1): termino = termino*(t-ti[f]) polinomio = polinomio + termino*factor # simplifica polinomio, multiplica los (t-ti) polinomio = polinomio.expand() # para evaluacion numérica pt = sym.lambdify(t,polinomio) # Puntos para la gráfica a = np.min(ti) b = np.max(ti) muestras = 101 ti_p = np.linspace(a,b,muestras) fi_p = pt(ti_p) # SALIDA print([titulo]) print(tabla) print('polinomio:') print(polinomio) # Gráfica plt.title('Interpolación polinómica') plt.plot(ti,fi,'o', label = 'Puntos') plt.plot(ti_p,fi_p, label = 'Polinomio') plt.legend() plt.show()
