s3Eva_IIT2019_T3 Preparación de terreno en refineria

Ejercicio: 3Eva_IIT2019_T3 Preparación de terreno en refineria

Se requiere usar el nivel inicial en la matriz, para restar del nivel requerido que es constante 220

Nivel inicio (m)	0	50	100	150	200
0	241	239	238	236	234
25	241	239	237	235	233
50	241	239	236	234	231
75	242	239	236	232	229
100	243	239	235	231	227

lo que genera la matriz de diferencias. El valor es positivo indica remoción, el valor negativo indica por rellenar.

Diferencia (m)	0	50	100	150	200
0	21	19	18	16	14
25	21	19	17	15	13
50	21	19	16	14	11
75	22	19	16	12	9
100	23	19	15	11	7

El volumen se puede calcular por un método en cada fila, y luego los resultados por columnas por otro método o el mismo.
Por ejemplo Simpson de 1/3

I= \frac{hx}{3}(f(x_0) +4f(x_1)+f(x_2))

con lo que se obtiene:

I_{fila}(0) = \frac{50}{3}(21 +4(19)+18) +\frac{50}{3}(18 +4(16)+14) =24750 I_{fila}(25) = = \frac{50}{3}(21 +4(19)+17) + \frac{50}{3}(17 +4(15)+13) = 23383,33 I_{fila}(50) = \frac{50}{3}(21 +4(19)+16) + \frac{50}{3}(16 +4(14)+11) = 22000 I_{fila}(75) = \frac{50}{3}(22 +4(19)+16) + \frac{50}{3}(16 +4(12)+5) =21850 I_{fila}(100) = \frac{50}{3}(23 +4(19)+15) + \frac{50}{3}(15 +4(11)+7) = 20483,33

y usando el otro eje, se completa el volumen usando dos veces simpson:

Volumen = \frac{h_y}{3}(f(x_0) +4f(x_1)+f(x_2)) Remover = \frac{25}{3}(24750 +4(23383,33)+22000) + + \frac{25}{3}(22000 +4(21850)+20483,33)=2251388,89

El signo lo trae desde la diferencia, y muestra el sentido del desnivel.

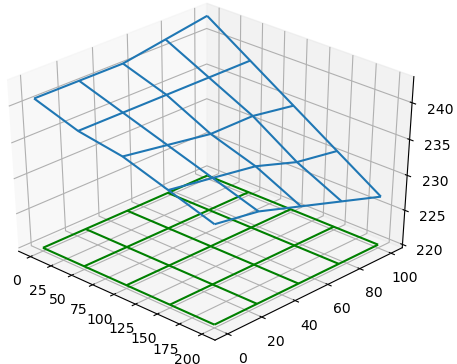
Se adjunta la gráfica de superficie en azul como referencia del signo,  respecto al nivel requerido en color verde.

Error de truncamiento

la cota del error de truncamiento se estima como O(h5)

error_{trunca} = -\frac{h^5}{90} f^{(4)}(z)

para un valor de z entre [a,b]

para cuantificar el valor, se puede usar la diferencia finita Δ4f, pues con la derivada sería muy laborioso.