Ejercicio: 3Eva_IIT2019_T4 completar polinomio de interpolación
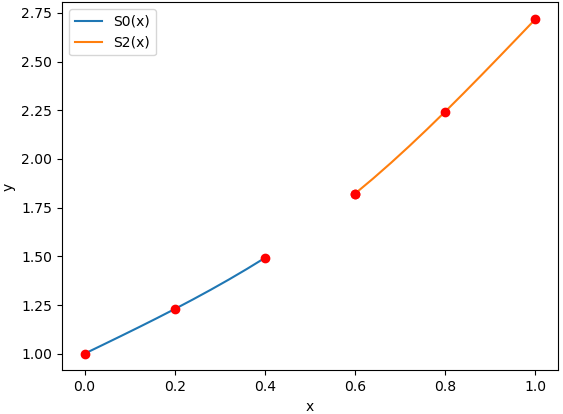
Para visualizar la solución, se plantea graficar los polinomios que están completos S0(x) y S2(x).
S_0(x) = 1 + 1.1186x + 0.6938 x^30.0 ≤ x ≤ 0.4
S_1(x) = 1.4918 + 1.4516(x-0.4) + c(x-0.4)^2 +d(x-0.4)^30.4 ≤ x ≤ 0.6
S_2(x) = 1.8221 + 1.8848(x-0.6) + +1.3336(x-0.6)^2 - 1.1113(x-0.6)^30.6 ≤ x ≤ 1.0
Como en trazadores cúbicos, lo que se usa es un polinomio por cada tramo muestreado para una curva contínua, etc. se tiene que los polinomios deben tener valores iguales en los puntos el eje x = 0.4 y 0.6
Por lo que se evalua con los polinomios completos:
S_0(0.4) = 1 + 1.1186(0.4) + 0.6938 (0.4)^3 = 1.4918432 S_2(0.6) = 1.8221 + 1.8848(0.6-0.6) + +1.3336(0.6-0.6)^2-1.1113(0.6-0.6)^3=1.8221Opción 1
Valores que se usan en los extremos del polinomio S1(x) para crear un sistema de dos ecuaciones y determinar los valores de c y d, completando el polinomio.
S_1(0.4) = 1.4918 + 1.4516(0.4-0.4) + c(0.4-0.4)^2 +d(0.4-0.4)^3como los términos de c y d se hacen cero, hace falta una ecuación.
S_1(0.6) = 1.4918 + 1.4516(0.6-0.4) + + c(0.6-0.4)^2 +d(0.6-0.4)^3 = 1.8221 1.8221 = 1.4918 + 1.4516(0.2) + c(0.2)^2 +d(0.2)^3 0,03998 = 0.04c +0,008dla otra ecuación se podría obtener usando la propiedad que las primeras derivadas de los polinomios deben ser iguales en los puntos x=0,4 y x= 0.6
S’0(0.2) =S’1(0.2)
Tarea: Desarrollar la siguiente ecuación y resolver
Opción 2
Si no recuerda la propiedad anterior, puede optar por usar otros conceptos para aproximar el resultado.
Si para el tramo en que se busca el polinomio se puede retroceder un tamaño de paso x = 0.2 y evualuar usando S0(0.2), se obtiene otropunto de referencia para crear un polinomio que pase por los mismos puntos.
S_0(0.2) = 1 + 1.1186*(0.2) + 0.6938 (0.2)^3Se aplica lo mismo para un tamaño de paso más adelante de x = 0.6 es x = 0.8m se evalua S2(0.8) y se tienen suficientes puntos para usar cualquier método de interpolación y determinar el polinomio para el tramo faltante.
S_2(0.8) = 1.8221 + 1.8848(0.8-0.6) + +1.3336(0.8-0.6)^2 - 1.1113(0.8-0.6)^3xi = [0. 0.2 0.4 ] S0(xi) = [1. 1.2292704 1.4918432] xi = [0.6 0.8 1. ] S2(xi) = [1.8221 2.2435136 2.7182728]
que permite hacer una tabla de puntos, y usando por ejemplo el método de interpolación de Lagrange con x entre [0.2, 0.8] se obtiene otra forma del polinomio buscado:
p(x)=1.2292704 \frac{(x-0.4)(x-0.6)(x-0.8)}{(0.2-0.4)(0.2-0.6)(0.2-0.8)} + +1.4918432\frac{(x-0.2)(x-0.6)(x-0.8)}{0.4-0.2)(0.4-0.6)(0.4-0.8)}+ +1.8221\frac{(x-0.2)(x-0.4)(x-0.8)}{(0.6-0.2)(0.6-0.4)(0.6-0.8)} + + 2.2435136\frac{(x-0.2)(x-0.4)(x-0.6)}{(0.8-0.2)(0.8-0.4)(0.8-0.6)}Tarea: continuar con el desarrollo
El literal b, requiere usar un metodo de búsqueda de raíces, para el cual se puede usar incluso bisección.
Tarea: continuar con el desarrollo