s3Eva_IT2010_T2 EDO problema con valor inicial dy/dx

Ejercicio: 3Eva_IT2010_T2 EDO problema con valor inicial dy/dx

Ecuación del problema:

(2y^2 + 4x^2)\delta x -xy \delta y =0

se despeja dy/dx:

(2y^2 + 4x^2)\delta x = xy \delta y \frac{\delta y}{\delta x} =\frac{2y^2 + 4x^2}{xy}

con valores iniciales de x₀ = 1, y₀=-2 , h=0.2 e intervalo [1,2]

Usando Runge-Kutta de 2do Orden

Iteración 1

K_1= h\frac{\delta y}{\delta x}(1,-2) =(0.2)\frac{2(-2)^2 + 4(1)^2}{(1)(-2)}= -1.2 K_2= h\frac{\delta y}{\delta x}(1+0.2,-2+(-1.2)) =(0.2)\frac{2(-2-1.2)^2 + 4(1+0.2)^2}{(1+0.2)(-2-1.2)}= -1.3667 y_1 = -2 + \frac{-1.2-1.3667}{2} = -3.2833 x_1 = x_0 + h = 1 + 0.2 = 1.2 error = O(h^3) = O(0.2^3) = 0.008

Iteración 2

K_1= h\frac{\delta y}{\delta x}(1.2,-3.2833) =(0.2)\frac{2(-3.2833)^2 + 4(1.2)^2}{(1.2)(-3.2833)}= -1.3868 K_2= h\frac{\delta y}{\delta x}(1.2+0.2,-3.2833+(-1.3868)) =(0.2)\frac{2(-3.2833+(-1.3868))^2 + 4(1.2+0.2)^2}{(1.2+0.2)(-3.2833+(-1.3868))}= -1.5742 y_2 = -3.2833 + \frac{-1.3868-1.5742}{2} = -4.7638 x_2 = x_1 + h = 1.2 + 0.2 = 1.4

Iteración 3

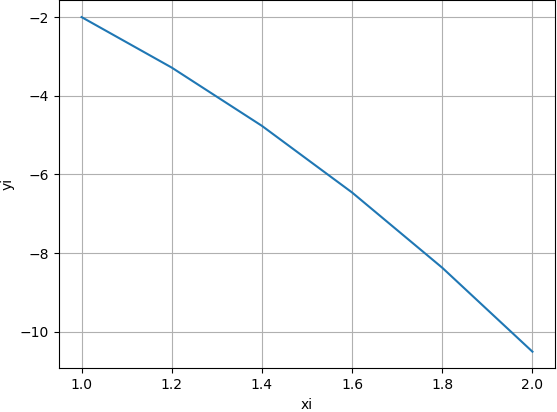
K_1= h\frac{\delta y}{\delta x}(1.4,-4.7638) =(0.2)\frac{2(-4.76383)^2 + 4(1.4)^2}{(1.4)(-4.7638)}= -1.5962 K_2= h\frac{\delta y}{\delta x}(1.4+0.2,-4.7638+(-1.5962)) =(0.2)\frac{2(-4.7638+(-1.5962))^2 + 4(1.4+0.2)^2}{(1.4+0.2)(-4.7638+(-1.5962))}= -1.7913 y_3 = -4.7638 + \frac{-1.5962-1.7913}{2} = -6.4576 x_3 = x_2 + h = 1.4 + 0.2 = 1.6

con lo que usando el algoritmo se obtiene la tabla y gráfica:

 [xi,       yi,       K1,     K2     ]
[[  1.      -2.       0.       0.    ]
 [  1.2     -3.2833  -1.2     -1.3667]
 [  1.4     -4.7638  -1.3868  -1.5742]
 [  1.6     -6.4576  -1.5962  -1.7913]
 [  1.8     -8.3698  -1.8126  -2.0119]
 [  2.     -10.5029  -2.032   -2.2342]

Algoritmo en Python

# 3Eva_IT2010_T2 EDO
import numpy as np
import matplotlib.pyplot as plt

# INGRESO
d1y = lambda x,y : (2*(y**2)+4*(x**2))/(x*y)
x0 = 1
y0 = -2
h = 0.2
a = 1
b = 2

# PROCEDIMIENTO
muestras = int((b -a)/h)+1
tabla = np.zeros(shape=(muestras,4),dtype=float)

i = 0
xi = x0
yi = y0
tabla[i,:] = [xi,yi,0,0]

i = i+1
while not(i>=muestras):
    K1 = h* d1y(xi,yi)
    K2 = h* d1y(xi+h,yi+K1)
    yi = yi + (K1+K2)/2
    xi = xi +h
    tabla[i,:] = [xi,yi,K1,K2]
    i = i+1
# vector para gráfica
xg = tabla[:,0]
yg = tabla[:,1]

# SALIDA
# muestra 4 decimales
np.set_printoptions(precision=4)
print(' [xi, yi, K1, K2]')
print(tabla)

# Gráfica
plt.plot(xg,yg)
plt.xlabel('xi')
plt.ylabel('yi')
plt.grid()
plt.show()

Tarea: Realizar con Runge Kutta de 4to Orden